A particle is moving in a straight line with constant acceleration. If x,y and z be the distances described by a particle during the pth, qth and rth second respectively, prove that
Let (u) be the initail velocity of the particle and (A) b its uniform acceleration . Using the
relation, Dn=u+a2(2n−1),wehave<br>a =u + A/2 (2 l -1 ) ….(i)<br>b=u + A/2 (2m -1)…(ii)<br> and c=u+A2(2n−1) ..(iii)
Subtract∈g(iii)om(ii),,<br> b-c = A/2 (2 m-2n) = A (m-n)<br>or a (m -n) =a 9b-c)//A<br>=(ab-ac)//A ...(v)
Subtract∈g(ii)om(i),<br> a-b =A/2 (2l -2m) =A (l-m)<br>or c( l-m) = c (a -b)//A = (ac-bc) //A......(vi)<br>Add∈g(iv),(v)and(iv),we≥t<br> a (m-n) = b (n-l) + c (l-m)<br>= (ab-ac)/A + (bc-ab)/A + (ac - bc)/A =0 .
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 SolvedExamples
46 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 SolvedExamples
31 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 SolvedExamples
17 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
A particle is moving in a straight line with constant acceleration. Then its acceleration is s−s'm−n where sand s' are the spaces described during the mth and the nth seconds respectively.
View SolutionA particle is moving in a straight line its speed depends on x as shown. The acceleration of particle is...
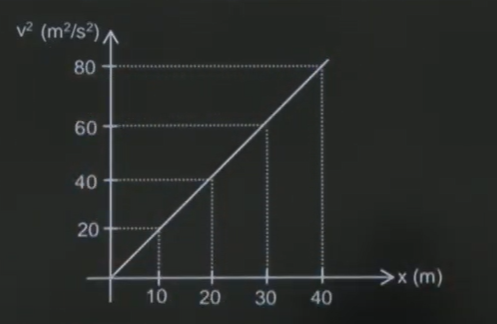
View Solution
Knowledge Check
For a particle moving in a straight line
AIf velocity is negative and acceleration is positive then speed increases.Bif velocity is positive and acceleration is negative then speed decreases.Cif velocity is zero at an instant then acceleration must also be zero at that instant.Dit is possible that speed of a particle is never zero in an interval of time, but average speed is zero.A particle is moving in a straight line with uniform velocity. Its acceleration is
ApositiveBnegativeCzeroDnone of theseA particle is moving in a straight line with uniform velocity. Its acceleration is
ApositiveBnegativeCzeroDnone of these
A particle at rest starts moving in a horizontal straight line with a uniform acceleration. The ratio of the distances covered during the fourth and third seconds is
View SolutionA particle moves in a straight line with constant acceleration under a constant force F. Select the correct alternative(s).
View SolutionA particle moves in a straight line with constant acceleration under a constant force F. Select the correct alternative(s).
View SolutionA particle moves in a straight line with a constant acceleration. It passing through a distance 135 m in t second. The value of t (in second) is
View SolutionA particle is moving along a straight line with constant acceleration. At the end of tenth second its velocity becomes 20m/s and in tenth second it travels a distance of 10m. Then the acceleration of the particle will be.
View Solution
