Do ( vec A + vec B) and (vec A-vec B) lien in the same plane. Explain.
Video Solution
Text Solution
Yes , (→A+→B) is represented by the diagonal of a parallelogram where two adjacent sides are represented by vectors →Aand→B. The diagonl passes therough the common tail of →Aand→B
(vec A-vec B) is represented by the other diaonal of the same parallelogram. If is not passing through the common tail of →Aand→B.
From above we note that both (vec A+ vec B), (vec A- vec B) lie in the plane of same parallelogram.
|
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 Short answer
30 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 5 Short answer
6 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 Short answer
26 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
Knowledge Check
Assertion : →A×→B is perpendicular to both →A+→B as well as →A−→B.
Reason: →A+→B as well as →A−→B lie in the plane contanining →Aand→B, but →A×→B lies perpendicular to the plane containing A and B.AAssertion is True, Reason is True, Reason is a correct explantion for AssertionBAssertion is True, Reason is True, Reason is not a correct explanaition for AssertionCAssertion is True, Reason is FalseDAssertion is False, Reason is False.Assertion: →A×→B is perpendicualr to both →A−→B as well as →A−→B
Reason: →A×→B as well as →A−→B lie in the plane containing →A and →B, but →A×→B lies perpendicular to the plane containing →A and →B.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both aseertion and reason are false.Vector product of three vectors is given by →A×(→B×→C)=→B(→A.→C)−→C(→A.→B)
The plane of vector →A×(→A×→B) lies in the plane ofA→AB→BC→A×→BD→A & →B
If (→a×→b)×(→c×→d).→a×→d=0 , then which of the following may be true? →a,→b,→cand→d are necessarily coplanar b.→a lies in the plane of →cand→d c. →b lies in the plane of →aand→d d. →c lies in the plane of →aand→d
View SolutionIf →A+→B=→A−→B, then vec B is a…………………………….. .
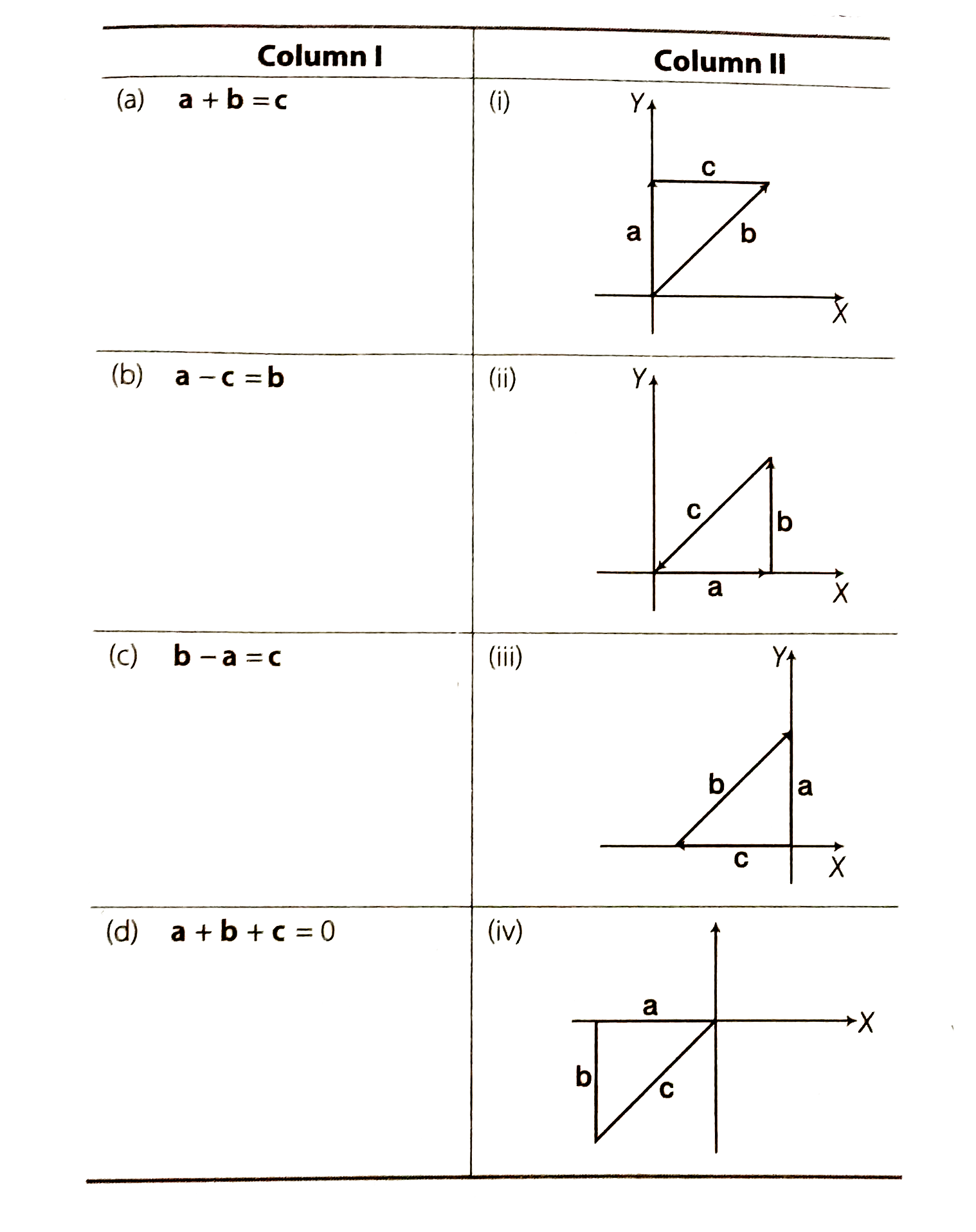
View SolutionGiven below in Column I are the relations between vectors a,b and c and in Column II are the orientations of a, b and c in the XY - plane . Match the relation in Column I to correct orientations in Column II.
View SolutionIf →A,→Band→C are vectors such that ∣∣→B∣∣−∣∣→C∣∣. Prove that [(→A+→B)×(→A+→C)]×(→B+→C).(→B+→C)=0
View SolutionIf (→a−→b).(→a+→b)=27and|→a|=2∣∣→b∣∣ find |→a|and∣∣→b∣∣
View Solution
