One second after the projection, a stone moves at an angle of 45∘ with the horzontal. Two seconds from the start, it is travelling horizontally. Find the angle of projection with the horizontal. (g=10 ms^(-2)).
After one second, let vx.vy be the horizontal and vertical coponent velocites of the projectile whose initial velcoity of projection (u) and angle of projection os θ then
vx=ucosθ and vy=usinθ−g×1=usinθ−g
As the resultant of →–––xand→vy makes an angle β(=45∘)withthehorizontal.so<br> tan beta =v_y/v_x = ( u sin theta-g)/( u cos theta) =tan 45^@or u sin theta- g = u or u (sin theta - cos theta ) = g ....(i)<br>Aftertwoseconds,theveticalcompo≠ntvelocityofprojecti≤becomeszero,sincethevelocityorprojecti≤ishorizontala>er→wseconds.So, u sin theta - 2 g = 0 oru2gsinθ
From (i) , (2 g)/( sin theta) (sin theta-cos theta) = gor 2 ( 1- cot theta ) = or 1-cot theta = 1/2<br>or cot theta 1- 1/2=1/2 ortanθ=2 or tˆa=tan−10(2).
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - Value based5videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Problems for practice25videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - Motion25videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
A particle is projected in the X−Y plane. 2sec after projection the velocity of the aprticle makes an angle 45%(∘) with the X−axis. 4sec after projection, it moves horizontally. Find the velocity of projection (use g=10ms−2).
View SolutionTwo seconds after projection, a projectile is travelling in a direction inclined at 30∘ to the horizontal. After one more second, it is travelling horizontally. Find the magnitude and direction of its velocity.
View Solution
Knowledge Check
- Question 1 - Select One
Projection angle with the horizontal is:
Atan−1(45)Btan−1(23)Ctan−1(54)Dtan−1(12) - Question 2 - Select One
A shot is fired at an angle θ to the horizontal such that it strikes the hill while moving horizontally. Find the initial angle of projection θ.
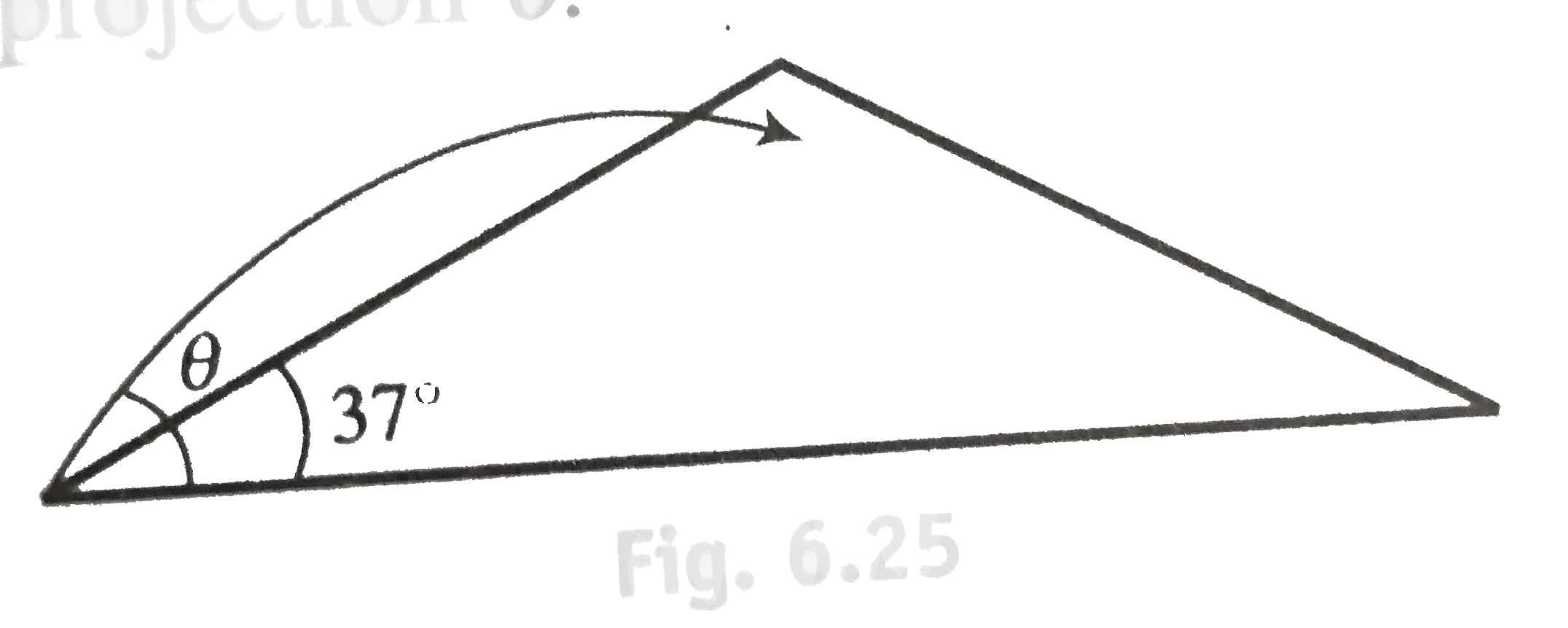 Atanθ=25Btanθ=38Ctanθ=32DNone of these
Atanθ=25Btanθ=38Ctanθ=32DNone of these - Question 3 - Select One
A projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
A60∘Btan−1(12)Ctan−1(√32)D45∘
A particle is projected from the ground . One second after the projection, the particle is found to be moving at an angle 45∘ with the horizontal . Speed of the particle becomes minimum two seconds after the projection . If angle of projection is tan−1(n), then what is the value of n ?
View SolutionTwo second after projection, a projectile is travelling in a direction inclined at 30∘ to the horizontal. After one more second, it is travelling horizontally. Find the magnitude and direction of the velocity of projection.
View SolutionTwo seconds after projection, a projectile is travelling in a direction inclined at 30∘ to the horizontal. After one more second, it is travelling horizontally. Find the magnitude and direction of its velocity.
View SolutionAfter one second the velocity of a projectile makes an angle of 45∘ with the horizontal. After another one more second its is travelling horizontally. The magnitude of its initial velocity and angle of projectile are
(g=10m/s2)View SolutionTwo second after projection, a projectile is travelling in a direction inclined at 30∘ to the horizontal. After one more second, it is travelling horizontally. Find the magnitude and direction of the velocity of projection.
View Solution

