A body is in accelerated motion. Is it possible that no work is done ? Give some example.
To determine whether a body in accelerated motion can do no work, we need to analyze the relationship between force, displacement, and the angle between them. Here’s a step-by-step solution to the question:
Step 1: Understand Work Done
The work done (W) by a force is given by the formula:
W=F⋅s⋅cos(θ)
where:
- W is the work done,
- F is the force applied,
- s is the displacement of the body,
- θ is the angle between the force and the displacement vector.
Step 2: Analyze the Condition for Zero Work
For work to be zero, the equation can be satisfied in two ways:
1. If the displacement s=0 (the body does not move).
2. If the angle θ=90∘ (the force is perpendicular to the displacement).
Step 3: Consider Accelerated Motion
In the case of accelerated motion, the body can still have a net force acting on it (which causes the acceleration). However, if the force is perpendicular to the direction of motion, the work done can still be zero.
Step 4: Example 1 - Uniform Circular Motion
Consider a body moving in a uniform circular motion. The centripetal force acting on the body is directed towards the center of the circle, while the displacement of the body is tangential to the circle. Here, the angle θ between the centripetal force and the displacement is 90∘. Thus:
W=F⋅s⋅cos(90∘)=0
Even though the body is in accelerated motion (due to centripetal acceleration), the work done by the centripetal force is zero.
Step 5: Example 2 - Earth Revolving Around the Sun
Another example is the Earth revolving around the Sun. The gravitational force exerted by the Sun on the Earth acts towards the Sun (radially inward), while the Earth's motion is tangential to its orbit. Again, the angle θ between the gravitational force and the displacement of the Earth is 90∘. Therefore, the work done by the gravitational force is also zero:
W=F⋅s⋅cos(90∘)=0
Conclusion
In conclusion, a body can be in accelerated motion and still have no work done on it if the force acting on it is perpendicular to its displacement. Examples include uniform circular motion and the Earth’s revolution around the Sun.
---
The work done (W) by a force is given by the formula:
W=F⋅s⋅cos(θ)
where:
- W is the work done,
- F is the force applied,
- s is the displacement of the body,
- θ is the angle between the force and the displacement vector.
For work to be zero, the equation can be satisfied in two ways:
1. If the displacement s=0 (the body does not move).
2. If the angle θ=90∘ (the force is perpendicular to the displacement).
In the case of accelerated motion, the body can still have a net force acting on it (which causes the acceleration). However, if the force is perpendicular to the direction of motion, the work done can still be zero.
Consider a body moving in a uniform circular motion. The centripetal force acting on the body is directed towards the center of the circle, while the displacement of the body is tangential to the circle. Here, the angle θ between the centripetal force and the displacement is 90∘. Thus:
W=F⋅s⋅cos(90∘)=0
Even though the body is in accelerated motion (due to centripetal acceleration), the work done by the centripetal force is zero.
Another example is the Earth revolving around the Sun. The gravitational force exerted by the Sun on the Earth acts towards the Sun (radially inward), while the Earth's motion is tangential to its orbit. Again, the angle θ between the gravitational force and the displacement of the Earth is 90∘. Therefore, the work done by the gravitational force is also zero:
W=F⋅s⋅cos(90∘)=0
In conclusion, a body can be in accelerated motion and still have no work done on it if the force acting on it is perpendicular to its displacement. Examples include uniform circular motion and the Earth’s revolution around the Sun.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.54videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Short Answer Question52videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - solved examples73videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
What is oscillatory motion ? Give some of its examples.
View SolutionWhat is meant by simple harmonic motion ? Give some examples.
View SolutionIs it possible for a body to be in accelerated motion under the action of a force but still no work is done by the force? Cite an example in support of your answer.
View SolutionIs it possible for a body to be accelerated without speeding up or slowing down ? If so, give an example.
View SolutionWhat is periodic motion ? Give some of its examples
View SolutionDefine uniform circular motion. Give some examples.
View SolutionConsider the compound (A) given below:
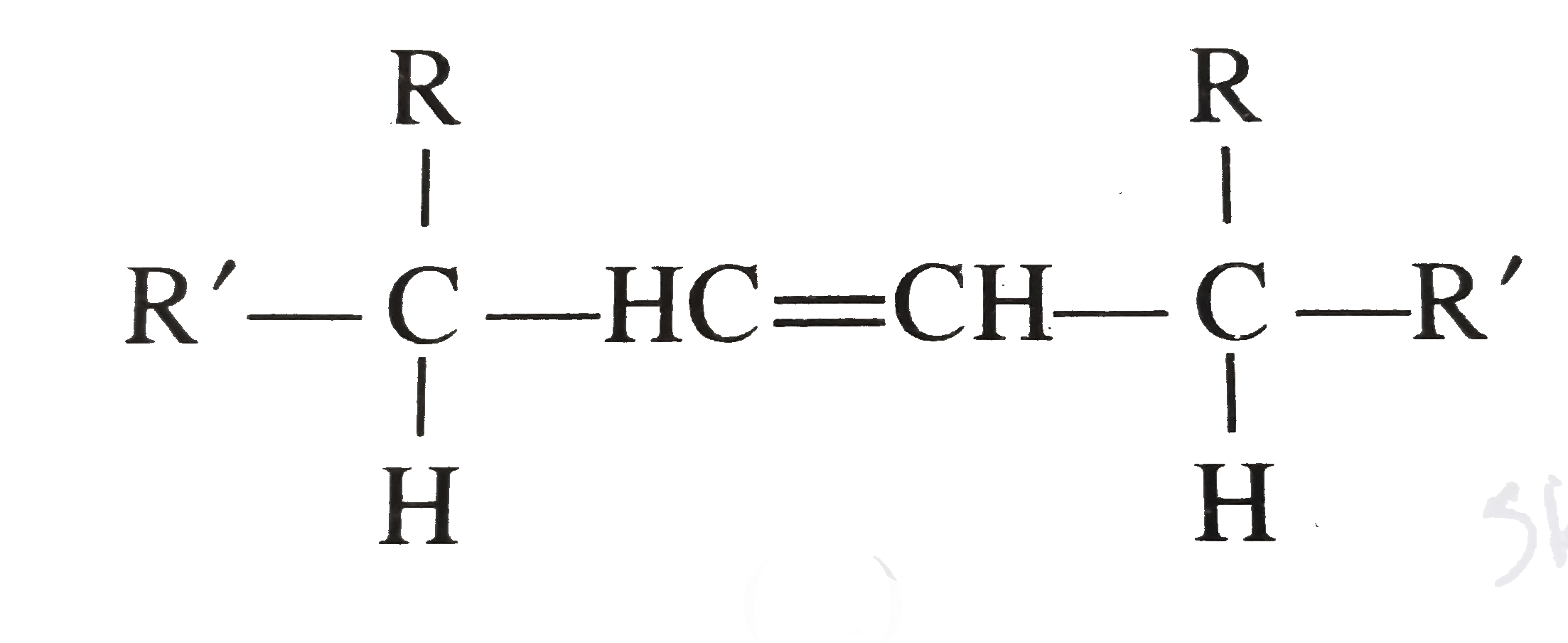
a. Give the total number of stereoisomers possible for (A).
b. If the stereochemistry about the double bond in (A) is cis, give the number of enantiomers possible for (A).
c. If the stereochemistry about the double bond (A) is trans, give the number of enantiomers possible for (A).
d. Give the total number of diastereomers possible for (A).
e. Give some examples of the types of (A).View SolutionWhen an object slides along a rough siuface, the force of friction does negative work on it. Is it ever possible for friction to do positive work? Give an example.
View SolutionWhenever a force is applied on a body, work is done.
View SolutionIs it possible that a force is acting on a body but still the work done is zero ? Explain giving one example.
View Solution

