A massless platform is kept on a light elastic spring as shown in figure. When a small stone of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the spring compresses by 0.01m. From what height should the stone be droppped to cause a compression of 0.04m in the spring ?

Video Solution

Text Solution

Verified by Experts

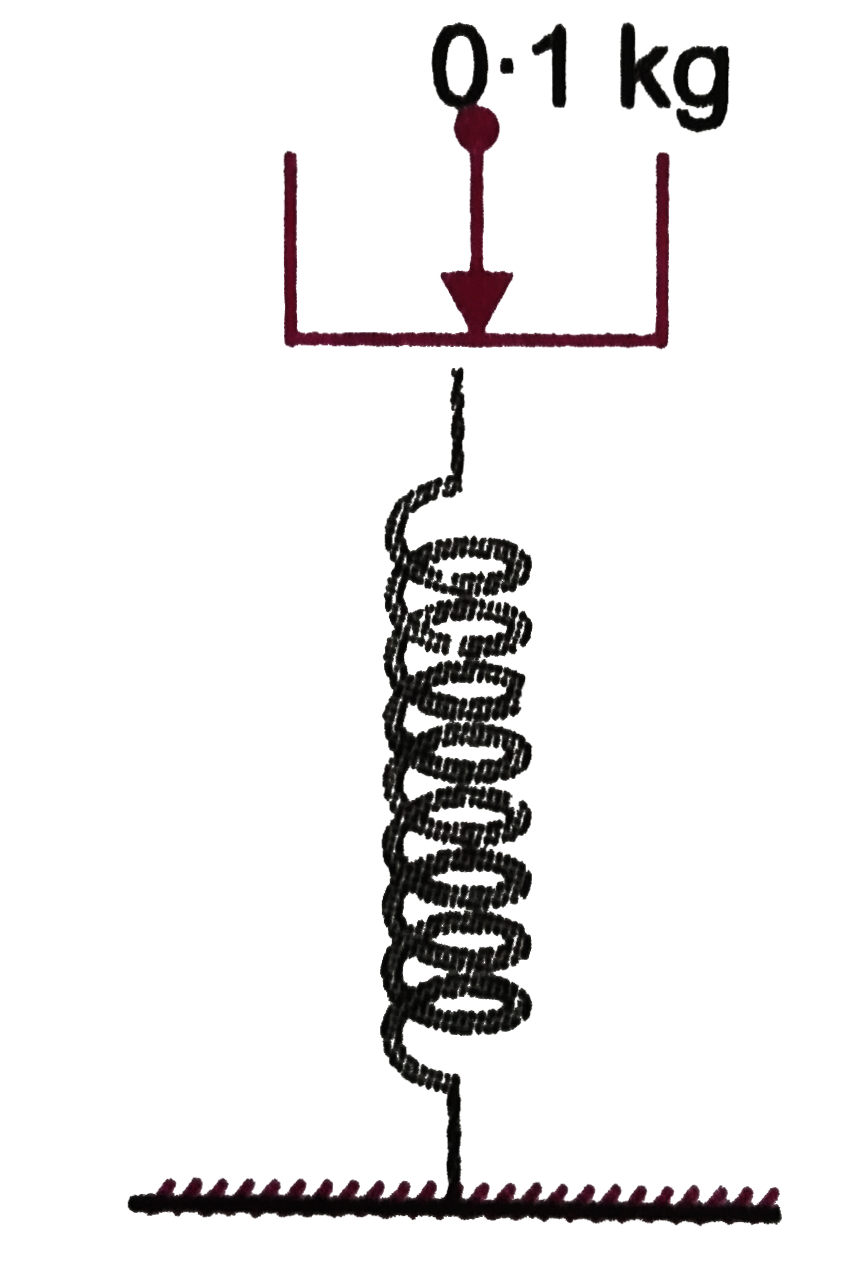
Here, $m = 0 k g, h = 0.24 m, x = 0.01 m .$
Clearly, loss in P.E. of stone $= m g (h + x),$ and gain in elstic P.E. of spring $= \frac{1}{2} k x^{2}$ .
$∴ M g (h + x) = \frac{1}{2} k x^{2}$ …(i)
Let $h^{'}$ be the height through which stone should be dropped to cause a compression of $x^{'} = 0.04 m$ .
$∴ m g (h^{'} + x^{'}) = \frac{1}{2} k x^{'} .^{2}$ ...(ii)
Dividing (i) by (ii), we get
$\frac{h + x}{h^{'} + x^{'}} = {(\frac{x}{x^{'}})}^{2} = {(\frac{0.01}{0.04})}^{2} = \frac{1}{16}$
$h^{'} x^{'} = 16 h + 16 x$
$h^{'} + 0.04 = 16 \times 0.24 + 16 \times 0.01$
$= 3.84 + 0.16 = 4.00$
$h^{'} = 4.00 - 0.04 = 3.96 m$

Updated on:21/07/2023

A massless platform is kept on a light elastic spring, as shown in the figure. When particle of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the particle strikes the pan, and the spring is compressed by 0.01 m. From what height should the particle be dropped to cause a compression of 0.04 m?

A0.96 m
B2.96 m
C3.96 m
D0.48 m
The two masses $m_{1}$ and $m_{2}$ are joined by a spring as shown. The system is dropped to the ground from a height. The spring will be

AStreched when $m_{2} > m_{1}$
BCompressed when $m_{2} < m_{1}$
Cneither compressed not stretched only when $m_{1} = m_{2}$
Dneither compressed not stretched regardless of the values of $m_{1}$ and $m_{2}$ .
When a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
A50 N/m
B100 N/m
C150 N/m
D200 N/m