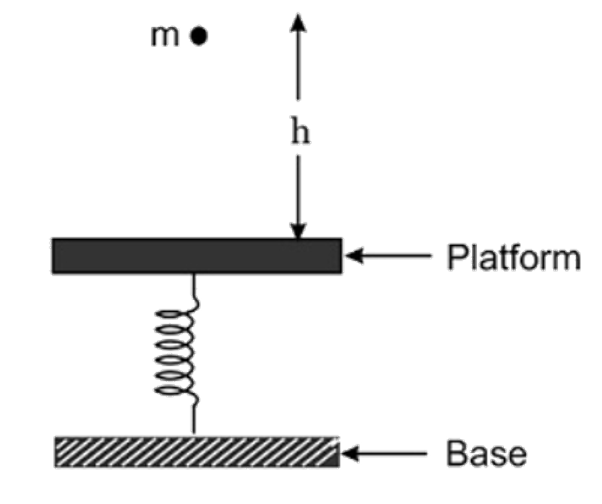
A ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
To find the spring constant K for the given scenario, we can follow these steps:
1. Understanding the Problem:
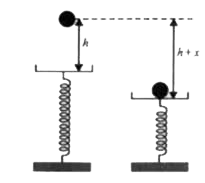
- A ball of mass m is dropped from a height h onto a platform that is fixed at the top of a vertical spring. The spring compresses by a distance x when the ball hits the platform.
2. Energy Considerations:
- We will use the principle of conservation of mechanical energy. The mechanical energy of the system is conserved if only conservative forces (like gravity and spring force) are acting.
3. Initial and Final States:
- Initially, when the ball is at height h, it has gravitational potential energy given by:
PEinitial=mgh
- When the ball compresses the spring by distance x, it has lost gravitational potential energy and gained spring potential energy. At maximum compression, the ball momentarily comes to rest, so its kinetic energy is zero.
4. Change in Potential Energy:
- The change in gravitational potential energy as the ball falls a total distance of h+x is:
ΔPEgravity=−mg(h+x)
- The potential energy stored in the spring when compressed by x is:
PEspring=12Kx2
5. Setting Up the Energy Conservation Equation:
- According to the conservation of energy:
ΔPEgravity+PEspring=0
- Substituting the expressions for potential energy:
−mg(h+x)+12Kx2=0
6. Rearranging the Equation:
- Rearranging gives:
12Kx2=mg(h+x)
7. Solving for the Spring Constant K:
- Multiply both sides by 2:
Kx2=2mg(h+x)
- Finally, solve for K:
K=2mg(h+x)x2
Final Result:
The spring constant K is given by:
K=2mg(h+x)x2
- A ball of mass m is dropped from a height h onto a platform that is fixed at the top of a vertical spring. The spring compresses by a distance x when the ball hits the platform.
- We will use the principle of conservation of mechanical energy. The mechanical energy of the system is conserved if only conservative forces (like gravity and spring force) are acting.
- Initially, when the ball is at height h, it has gravitational potential energy given by:
PEinitial=mgh
- When the ball compresses the spring by distance x, it has lost gravitational potential energy and gained spring potential energy. At maximum compression, the ball momentarily comes to rest, so its kinetic energy is zero.
- The change in gravitational potential energy as the ball falls a total distance of h+x is:
ΔPEgravity=−mg(h+x)
- The potential energy stored in the spring when compressed by x is:
PEspring=12Kx2
- According to the conservation of energy:
ΔPEgravity+PEspring=0
- Substituting the expressions for potential energy:
−mg(h+x)+12Kx2=0
- Rearranging gives:
12Kx2=mg(h+x)
- Multiply both sides by 2:
Kx2=2mg(h+x)
- Finally, solve for K:
K=2mg(h+x)x2
The spring constant K is given by:
K=2mg(h+x)x2
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:NCERT( Multiple choide questions-1)
Explore 21 Videos
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:JEE (Main and Advanced)
Explore 82 Videos
- WORK, ENERGY AND POWERBook:PRADEEPChapter:WORK, ENERGY AND POWERExercise:Fill in the blanks
Explore 10 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
A particle of mass m=1kg is dropped from a height h=40cm on a light horizontal platform fixed to one end of an elastic spring, the other being fixed to a base, as shown in the diagram. The particle collides with the platform and sticks to it. As a result, the spring is compressed by an amount x=10cm. What is the force constant of the spring?
(Take g=10ms−2)
View SolutionA block of mass m is relesed from rest from a height h onto a smooth sledge of mass M fitted with an ideal spring of stiffness k.

View Solution
Knowledge Check
A ball of mass m is dropped from a heighth on a platform fixed at the top of a vertical spring, as shown in figure. The platform is depressed by a distance x. Then the spring constant is
 Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)
Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
Amg(h+d)+12kd2Bmg(h+d)−12kd2Cmg(h−d)−12kd2Dmg(h−d)+12kd2A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
Amg(h+d)+12kd2Bmg(h+d)−12kd2Cmg(h−d)−12kd2Dmg(h−d)+12kd2
A block of massm, initally at rest is dropped from a height h onto a spring whose force constant is K. Find the maximum distance x through which the spring will be compressed.
View SolutionA vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
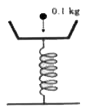
View SolutionA massless platform is kept on a light elastic spring, as shown in the figure. When particle of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the particle strikes the pan, and the spring is compressed by 0.01 m. From what height should the particle be dropped to cause a compression of 0.04 m?
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
View Solution
