A rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
mgl
mgl/2
mgl4
2mgl
To solve the problem of calculating the work done in making a rod of mass m and length l stand on one end, we can follow these steps:
1. Understanding the Initial Position:
- The rod is initially lying horizontally on the table. In this position, the center of mass of the rod is at a height of 0 above the ground.
2. Identifying the Center of Mass:
- The center of mass of a uniform rod of length l is located at its midpoint. Therefore, the height of the center of mass from the ground when the rod is lying flat is:
\(
h_{\text{initial}} = 0
\)
3. Final Position of the Rod:
- When the rod is made to stand on one end, the center of mass is raised to a height of \( \frac{l}{2} \) (half the length of the rod).
4. Calculating Initial Potential Energy:
- The initial potential energy (PE_initial) when the rod is lying flat is given by:
\(
PE_{\text{initial}} = mgh_{\text{initial}} = mg \cdot 0 = 0
\)
5. Calculating Final Potential Energy:
- The final potential energy (PE_final) when the rod is standing on one end is given by:
\(
PE_{\text{final}} = mgh_{\text{final}} = mg \cdot \frac{l}{2}
\)
6. Calculating the Work Done:
- The work done (W) in raising the rod is equal to the change in potential energy:
\(
W = PE_{\text{final}} - PE_{\text{initial}} = mg \cdot \frac{l}{2} - 0 = mg \cdot \frac{l}{2}
\)
Final Answer:
The work done in making the rod stand on one end is:
\(
W = \frac{mgl}{2}
\)
- The rod is initially lying horizontally on the table. In this position, the center of mass of the rod is at a height of 0 above the ground.
- The center of mass of a uniform rod of length l is located at its midpoint. Therefore, the height of the center of mass from the ground when the rod is lying flat is:
\(
h_{\text{initial}} = 0
\)
- When the rod is made to stand on one end, the center of mass is raised to a height of \( \frac{l}{2} \) (half the length of the rod).
- The initial potential energy (PE_initial) when the rod is lying flat is given by:
\(
PE_{\text{initial}} = mgh_{\text{initial}} = mg \cdot 0 = 0
\)
- The final potential energy (PE_final) when the rod is standing on one end is given by:
\(
PE_{\text{final}} = mgh_{\text{final}} = mg \cdot \frac{l}{2}
\)
- The work done (W) in raising the rod is equal to the change in potential energy:
\(
W = PE_{\text{final}} - PE_{\text{initial}} = mg \cdot \frac{l}{2} - 0 = mg \cdot \frac{l}{2}
\)
The work done in making the rod stand on one end is:
\(
W = \frac{mgl}{2}
\)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Comprehension
9 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Integer Type Questions
9 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - NCERT( Multiple choide questions-1)
21 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If the chain is limiting equlibrium, what is the coefficient of friction for the contact between table and chain?
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

What is the speed of the chain, when it just loses contact with the table?
View Solution
Knowledge Check
A uniform rod of mass 2kg and length l is lying on a horizontal surface. If the work done in raising one end of the rod through an angle 45∘ is 'W', then the work done in raising it further 45∘ is
AWB√2WCW√2D(√2−1)WA metre scale of mass 200 g, is lying on a horizontal table. What is the work done by student in making it stand vertically on one of its ends?
A2JB1.5JC1JD2.5JA rod of mass M and length l is placed on a smooth horizontal table and is hit by a ball moving horizontally and prependicular to length of rod and sticks to it Then conservation of angular momentum can be applied:
AAbout any point on the rodBAbout a point at the centre of the rodCAbout end point of the rodDNone
A uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If a gentale pull is given to hanging end, it will start moving down. What is the change in gravitational potential energy of the chain, as it jist leaves the table?
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:
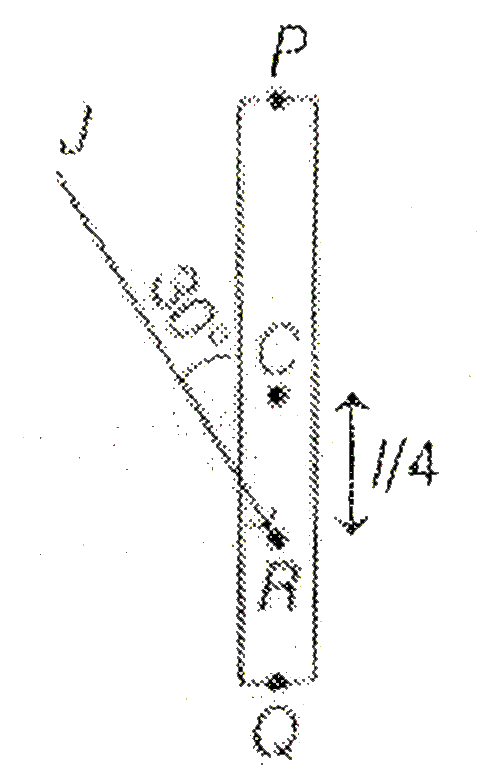
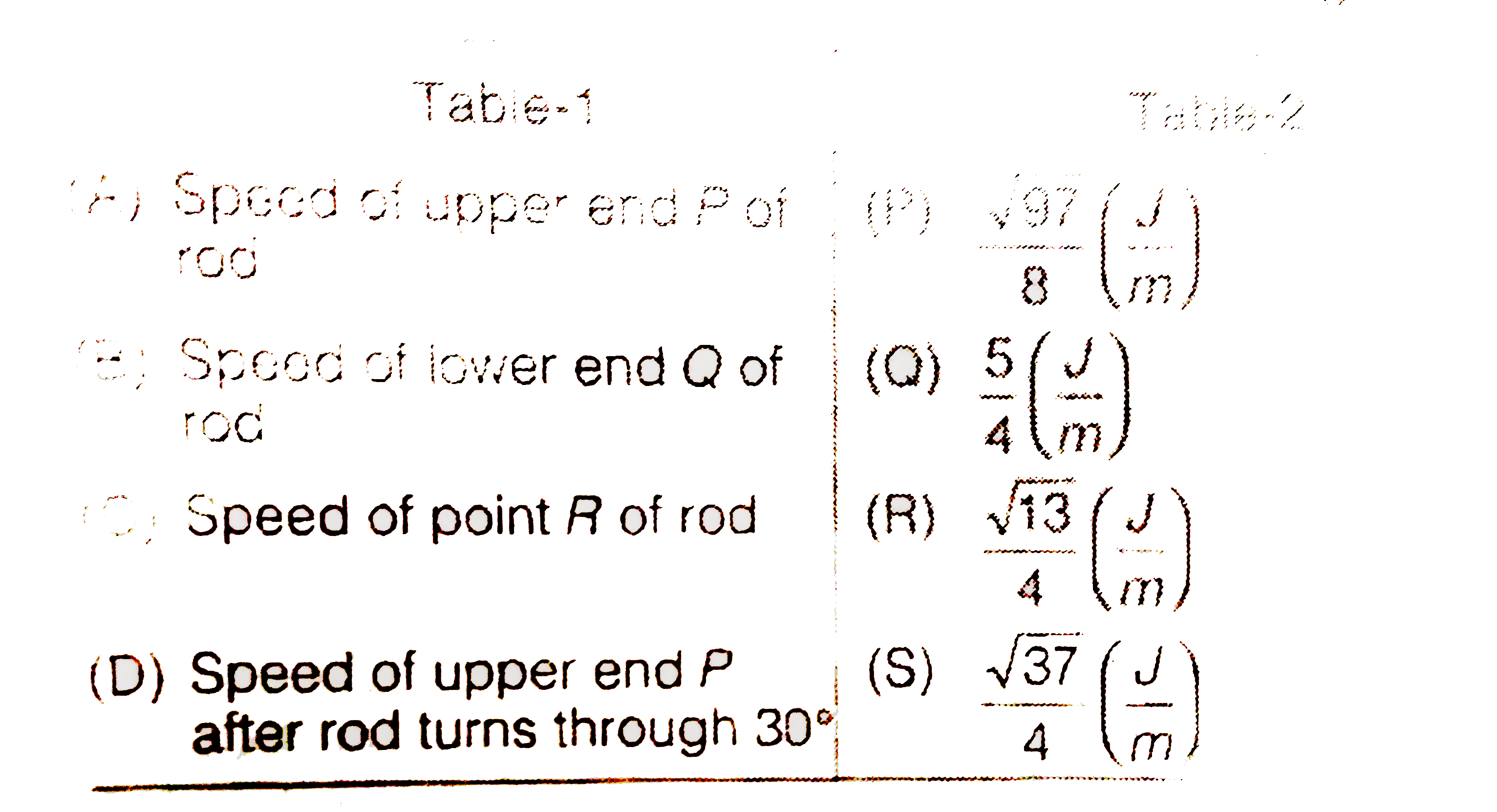
View SolutionA unifrom rod of mass m and length L is kept on a horizontal table with L4 length on the table. The end B is tied to a string as shown in the figure. The string attached to the end B is cut and the rod starts rotating about point C. Find the normal reaction from the table on the earth as soon as the string is cut.

View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View Solution
