A ball moving with a speed of 9m/s strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of 30∘ with the original line of motion. Find the speeds of the two balls after collision.
The correct Answer is:A
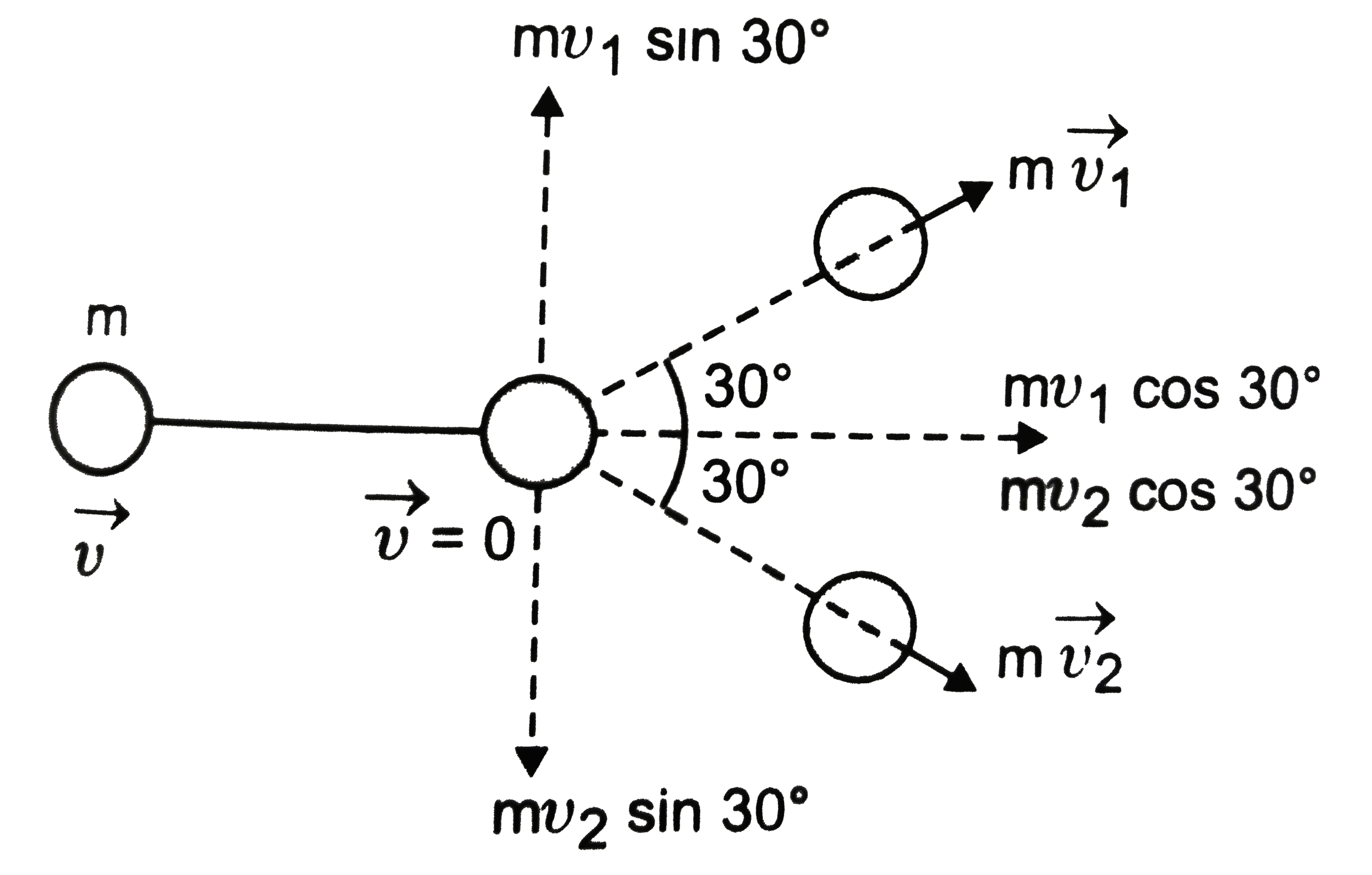
As shown in figure.
application of the law of conservation of linear momentum perpendicular to intial line of motion, gives
0=mυ1sin30∘−mυ2sin30∘∴υ1=υ2
Applying the same principle along the line of motion,
m×υ+m×0=2mυ1cos30∘+mυ2cos30∘
m×6+m×0=2mυ1cos30∘=2mυ1√32
υ1=6√3=2√3m/s
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Comprehension9videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Integer Type Questions9videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - NCERT( Multiple choide questions-1)21videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
A ball moving with a speed of 9ms−1 strikes an identical ball such that after the collision the direction of each ball makes and angle 30∘ with the original line of motion. Find the speeds of the two balls after the collision.
View SolutionA spherical body moving with a speed of 10 m/s strikes another identical body at rest such that after collision , the direction of motion of each ball makes an angle of 15∘ with the original direction of motion .
Calculate the speed of each body after collision .View Solution
Knowledge Check
- Question 1 - Select One
A ball moving with a speed of 10 m s−1 strikes an identical ball such that after the collision the direction of each ball makes an angle 45∘ with the original line of motion. Find the speeds of the two balls after the collision.
Av1=5√2 m/s,v2=10√2 m/sBv1=10√2 m/s,v2=10√2 m/sCv1=5√2 m/s,v2=5√2 m/sDv1=3√2 m/s,v2=10√2 m/s - Question 2 - Select One
A ball , moving with a speed of 10√3m/s , strikes an identical stationary ball such that after the collision , the direction of each ball makes an angle of 30∘with the original line of motion. The speeds of two balla after the collision are , respectively.
A5m/s,10m/sB10m/s,5m/sC5m/s,5m/sD10m/s,10m/s - Question 3 - Select One
A ball moving with velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at an angle of 30∘ with the original line of motion. What are the speeds of the balls after the collision ?
A√32msecB3msecC2√3msecD√3msec
A ball moving with a speed of 9m/s strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of 30∘ with the original line of motion. Find the speeds of the two balls after collision.
View SolutionA ball moving with a velocity 12m/s strikes an identical ball at rest.After collision both balls move in directions making 300 with original direction of motion.speeds of the balls after collision are (in ms−1) ?
View SolutionA ball moving with a velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at angle of 30∘ with the original line of motion. Assuming that the collision is elastic, what are the speeds of the balls after the collision?
View SolutionA billiard ball moving at a speed 2m/s strikes an identical ball initially at rest, at a glancing blow. After the collision one ball is found to be moving at a speed of 1m/s at 60∘ with the original line of motion. The velocity of the other ball shall be -
View SolutionA ball A moving with a velocity 5 m/s collides elastically with another identical ball at rest such that the velocity of A makes an angle of 30∘ with the line joining the centres of the balls. Then consider following statements :
(A) Balls A an B move at right angles after collision
(B) kinetic energy is conserved
(C) speed of A after collision is (5/2) m/s
(D) speed of B after collision is (5√3/2) m/s
Select correct alternative :-View Solution