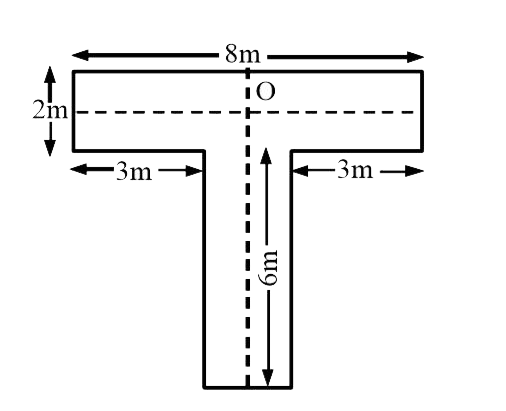
Find the position of centre of mass of the T-shaped plate from O, in Fig.

Suppose σ is mass per unit area of the plate.
∴ Mass of horizontal portion =8×2σ=16σ
Mass of vertical portion =6×2σ=12σ
Centre of mass O1 of horizontal portion is such that OO1=1m.
Centre of mass O2 of vertical portion is such that OO2=2+3=5m.
If y is distance of cm of T-shaped plate from O, then
y=16σ×1+12σ×516σ+12σ=76σ28σ=2.71m
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE B
2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE C
2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE A
2 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
The distance of the centre of mass of the T-shaped plate from O is :
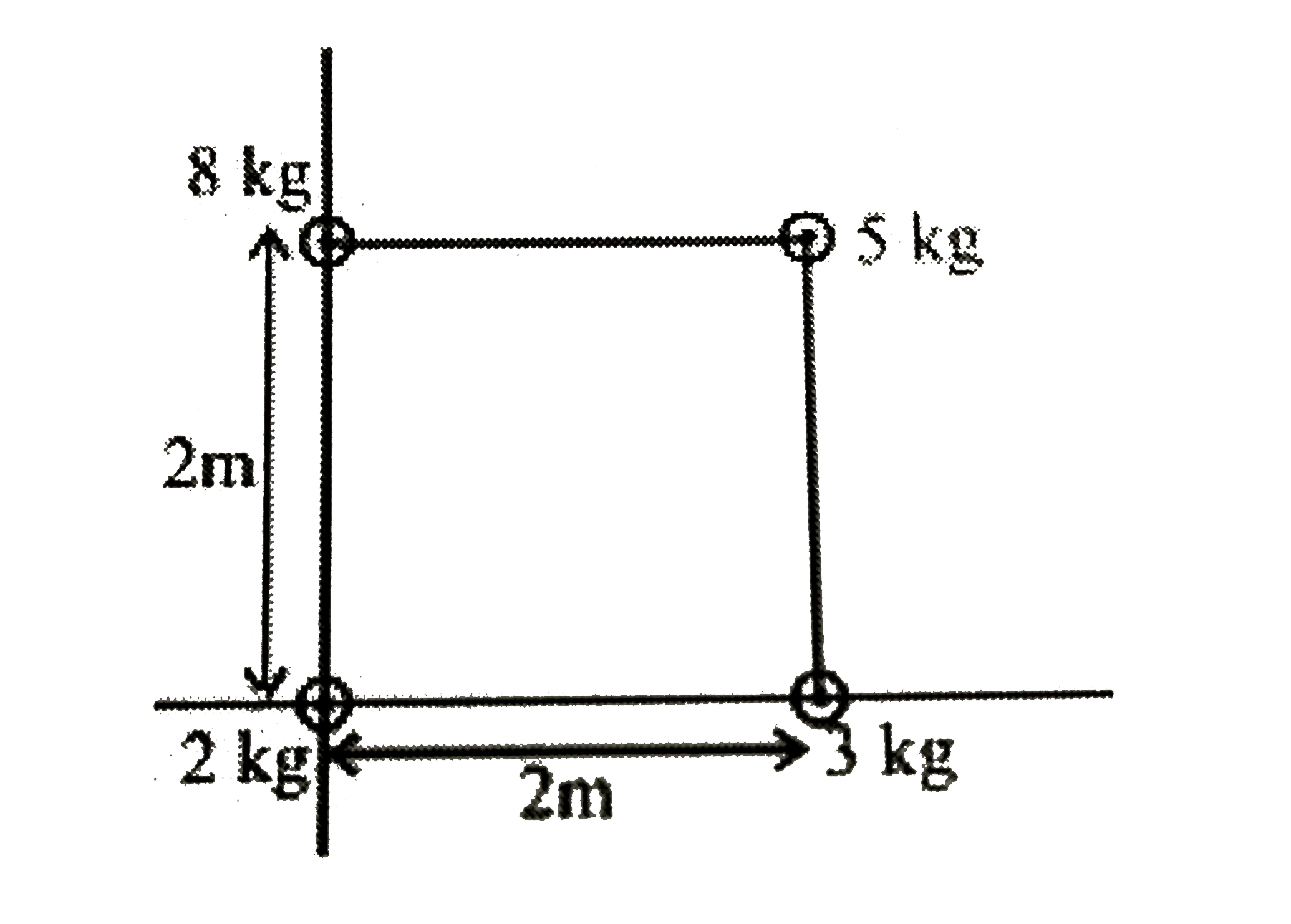
View SolutionPosition of the centre of mass is :-
View SolutionFind out the position of centre of mass of two particle system.
View SolutionFind the position of centre of mass of the section shown in figure

View SolutionFind the position of centre of mass of the uniform planner sheet shown in figure with respect to the origin (O) -
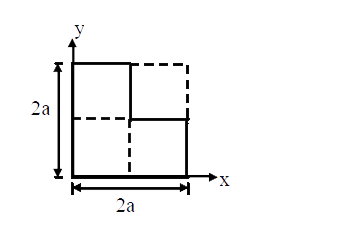
View SolutionFind out the position of centre of mass of the figure shown below.
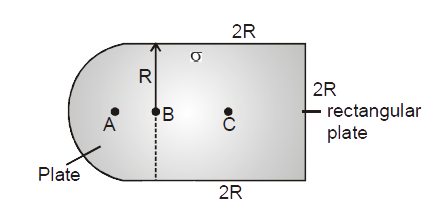
View SolutionFind the position of centre of mass of the uniform lamina shown in figure.
View SolutionFind the position of centre of mass of the uniform lamina shown in figure. If the mass density of the lamina is σ.

View SolutionThe distance of the centre of mass of T-shaped uniform plate from O is :
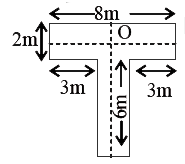
View SolutionA square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find

the position of centre of mass of the remaining portion from the centre O.
View Solution
