A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9∘and53.1∘ respectively. The bar is 2m long. Calculate the distance d of the centre of gravity of the bar from its left end.
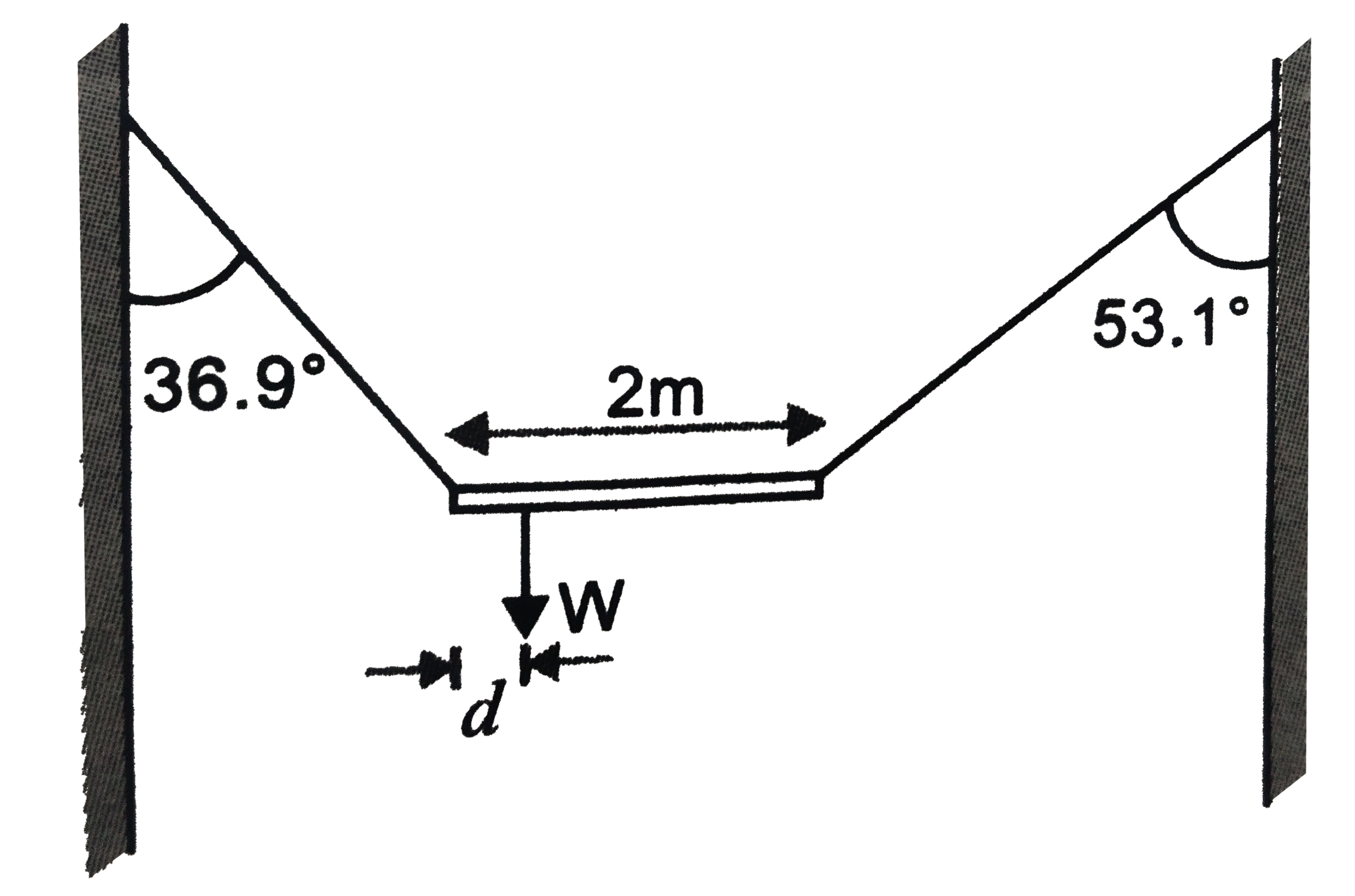
As is clear from Fig. θ1=36.9∘,θ2=53.1∘
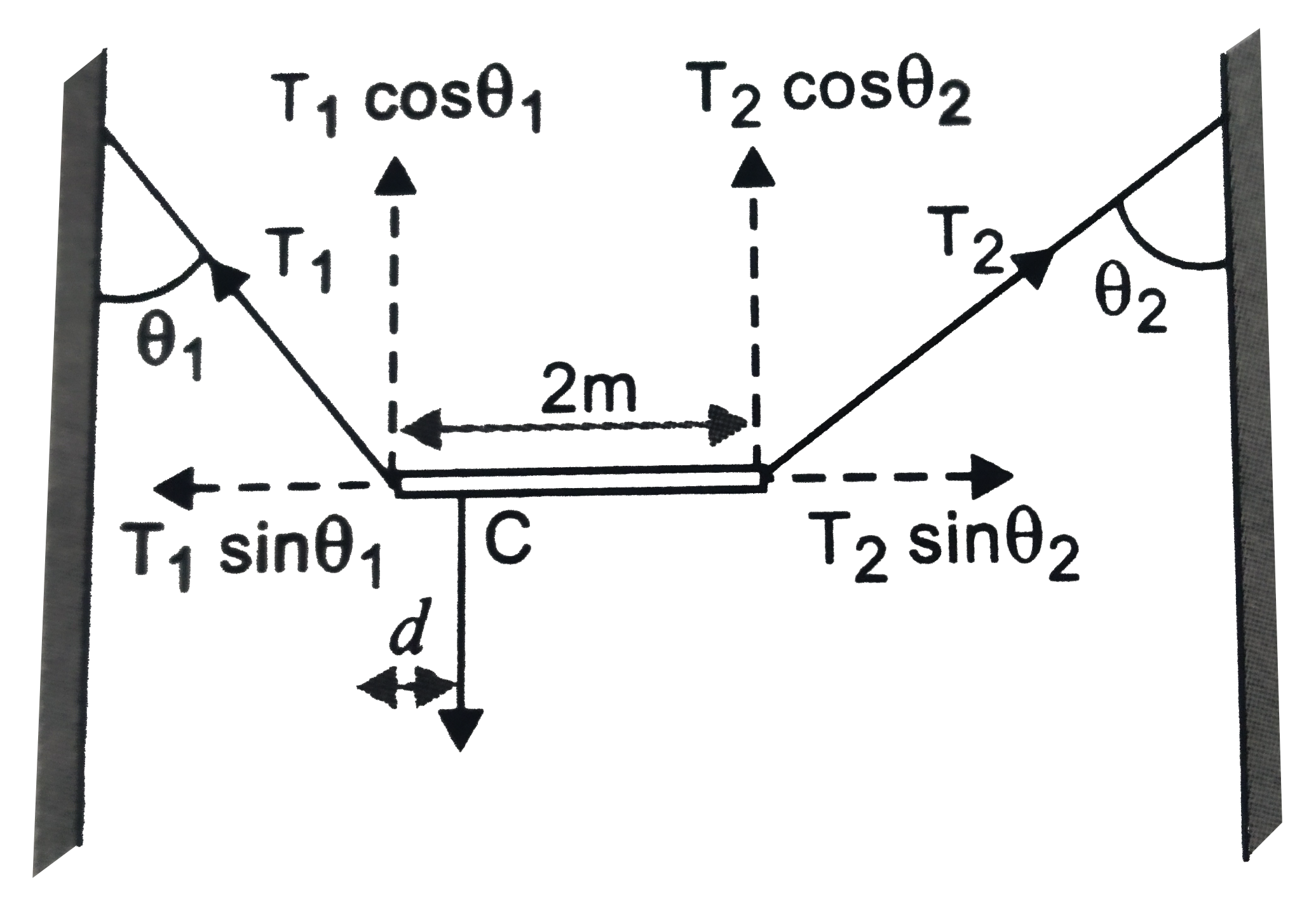
If T1,T2 are the tensions in the strings, then for equilibrium along the horizontal, T1sinθ1sinθ2
or T1T2=sinθ2sinθ1=sin53.1∘sin36.9∘=0.74070.5477=1.3523
Let d be the distance of centre of gravity C of the bar from the left end.
For rotational equilibrium about C,
T1cosθ1×d=T2cosθ2(2−d)
T1cos36.9∘×d=T2cos53.1∘(2−d)
T1×0.8366d=T2×0.6718(2−d)
Put T1=1.3523T2 and solve to get d=0.645m
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ADDITIONAL EXERCISES
11 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - QUESTIONS
15 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ADVANCED PROBLEMS FOR COMPETITIONS
20 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A non-uniform bar of weight W is suspended at rest by two string of negligible weights as shown in figure. The angle made by the string with the vertical are 36.9∘ and 53.1∘ respectively. The bar 2m long. Calculate the distance of the centre of gravity (in cm ) of the bar from it left end.
'(##CEN_KSR_PHY_JEE_C09_E01_033_Q19##)'
View Solution
A uniform rod of mass m and length l is held horizontally by two vertical strings of negligible mass, as shown in the figure.
(a). Immediately after the right string is cut, what is the linear acceleration of the end of the rod?
(b). Of the middle of the rod?
(c). Determine the tension in the left string immediately after the right string is cut.
View Solution
Knowledge Check
A non-uniform bar of weight w is suspended at rest by two strings of negligible weight as shown in figure. The angles made by the strings with the vertical are 37∘ and 53∘ respectively. The bar is 2m long. Calculate the distance d of the centre of gravity of the bar from its left end. given sin37∘=3/5 and sin53∘=4/5
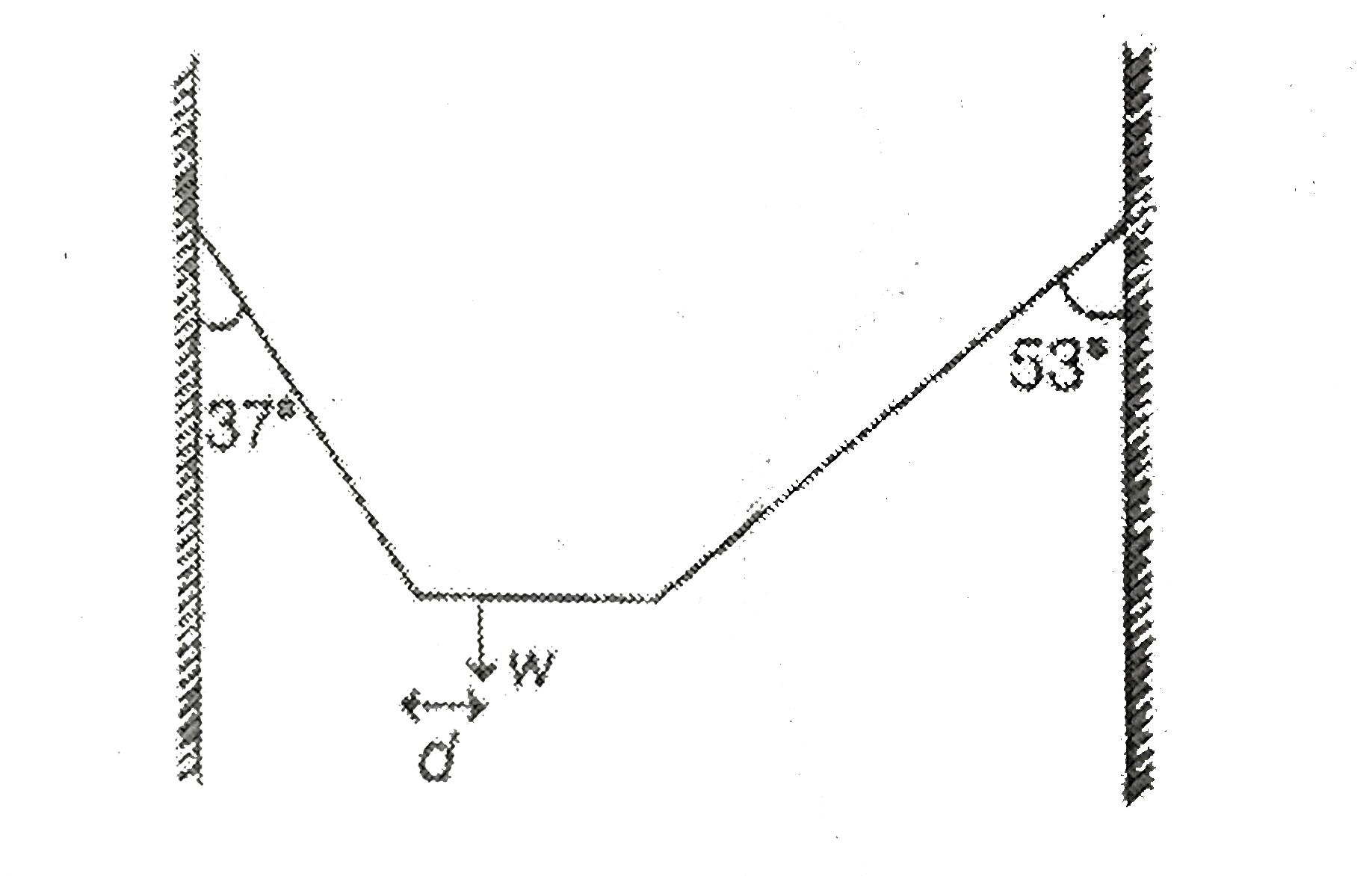 A72cmB64cmC100cmD40cm
A72cmB64cmC100cmD40cmA non-uniform bar of weight W and weight L is suspended by two strings of neigligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively.
The distance d of the centre of gravity of the bar from left end is.
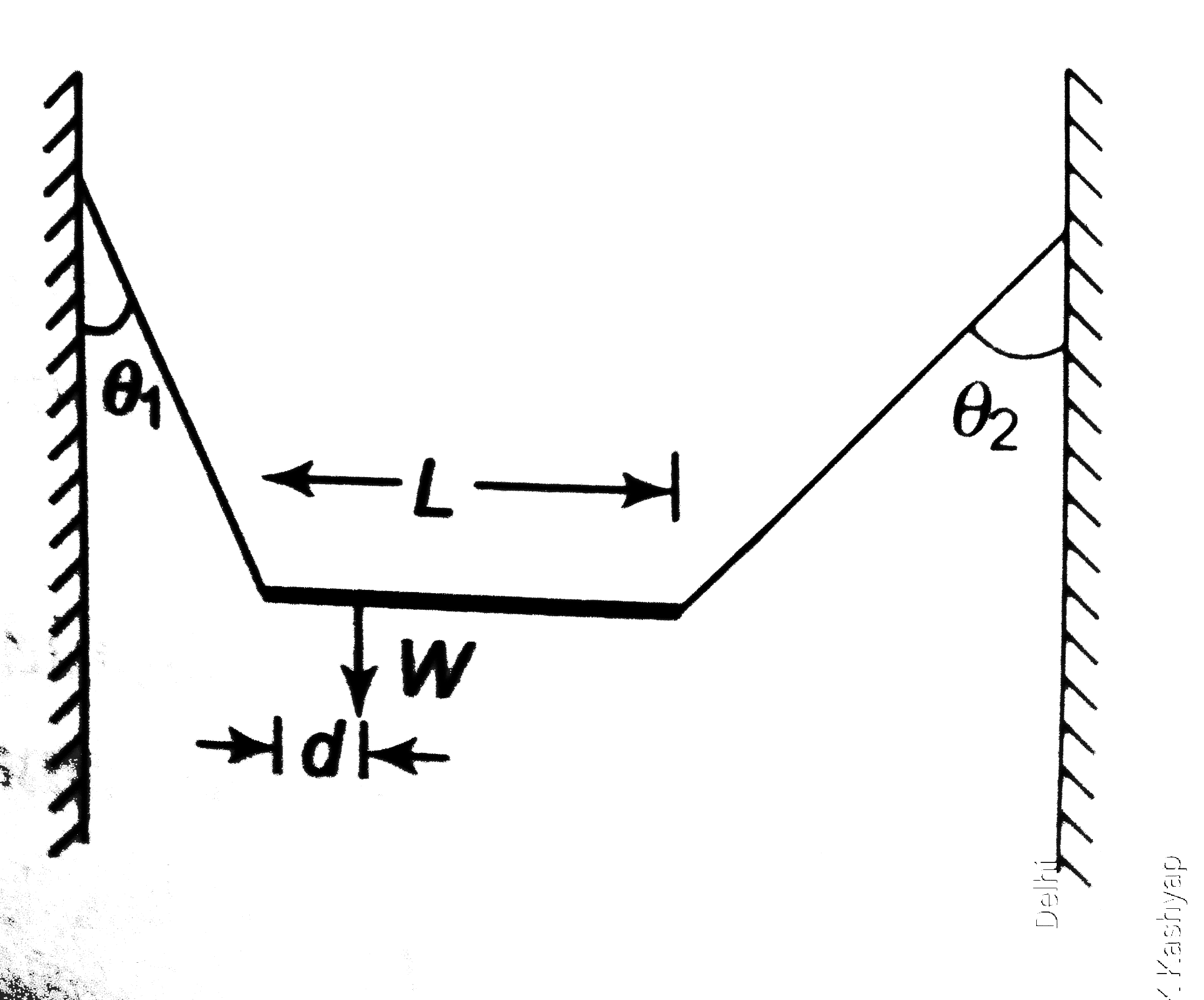 .AL(tanθ1+tanθ2tanθ1)BL(tanθ1tanθ1+tanθ2)CL(tanθ2tanθ1+tanθ2)DL(tanθ1+tanθ2tanθ2)
.AL(tanθ1+tanθ2tanθ1)BL(tanθ1tanθ1+tanθ2)CL(tanθ2tanθ1+tanθ2)DL(tanθ1+tanθ2tanθ2)A uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :
 AmgBmg4Cmg2Dmg3
AmgBmg4Cmg2Dmg3
A uniform rod of length 15 cm is suspended from a fixed point by two strings of length 9 cm and 12 cm attached at its ends. If the inclination of the rod to the vertical is θ then sinθ is equal to
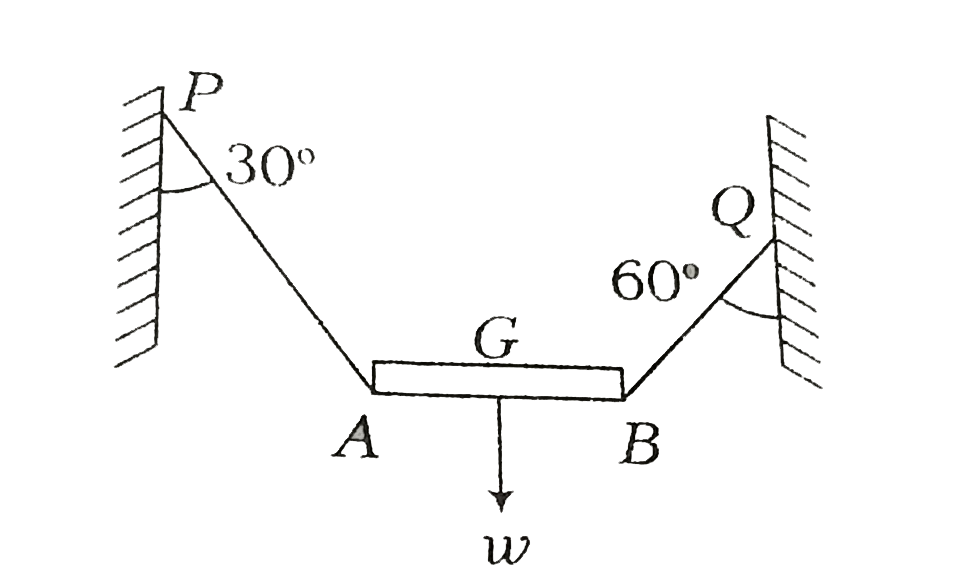
View SolutionA non-uniform rod AB of weight w is supported horizontally in a vertical plane by two light strings PA and QB as shown in the figure.G is the centre of gravity of the rod. If PA and QB make angles 30∘ and 60∘ respectively with the vertical, the ratio AGGB is
View SolutionA horizontal heavy uniform bar of weight W is supported at its ends by two men. At the instant, one of the men lets go off his end of the rod, the other feels the force on his hand changed to
View Solution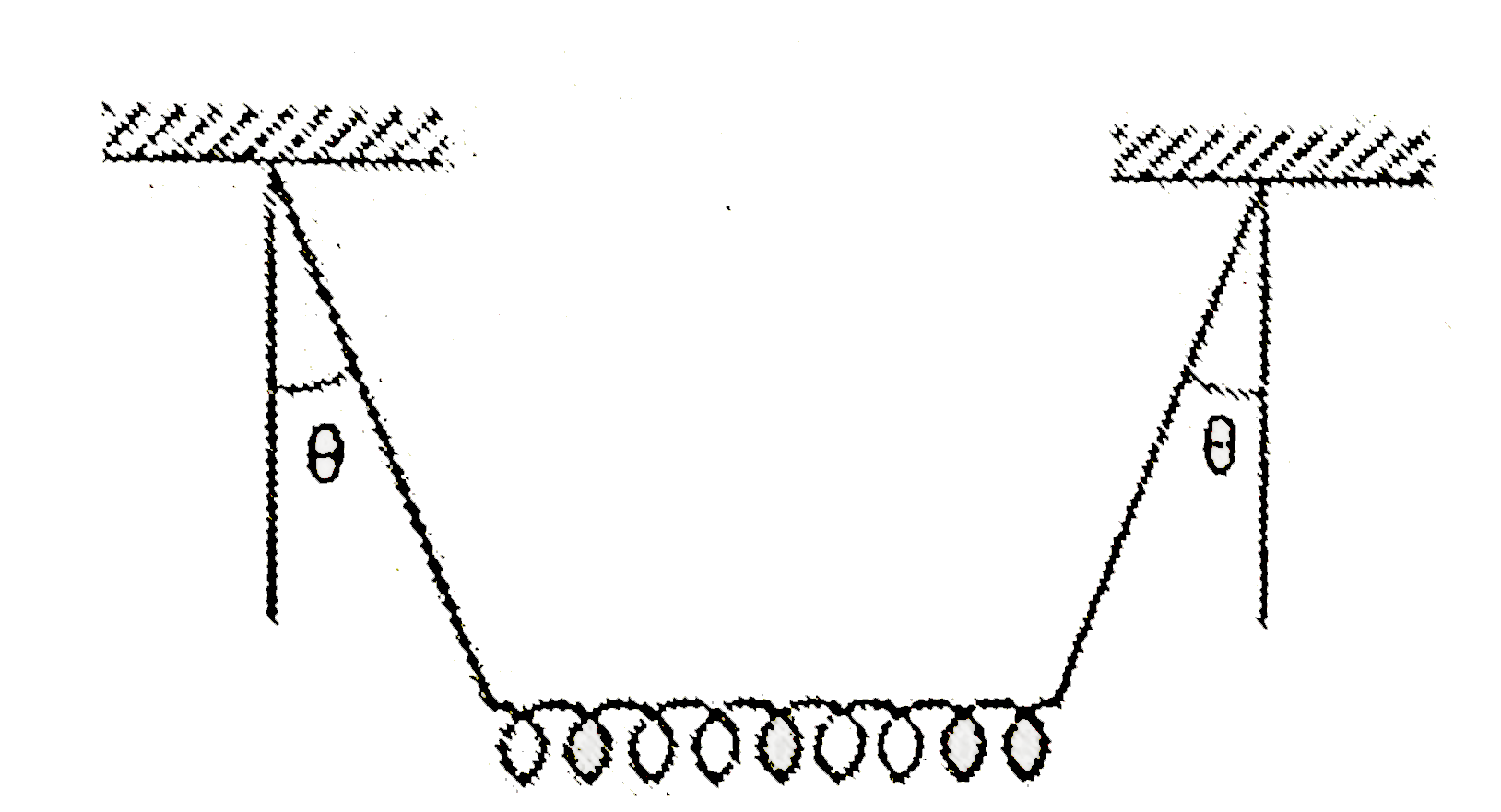
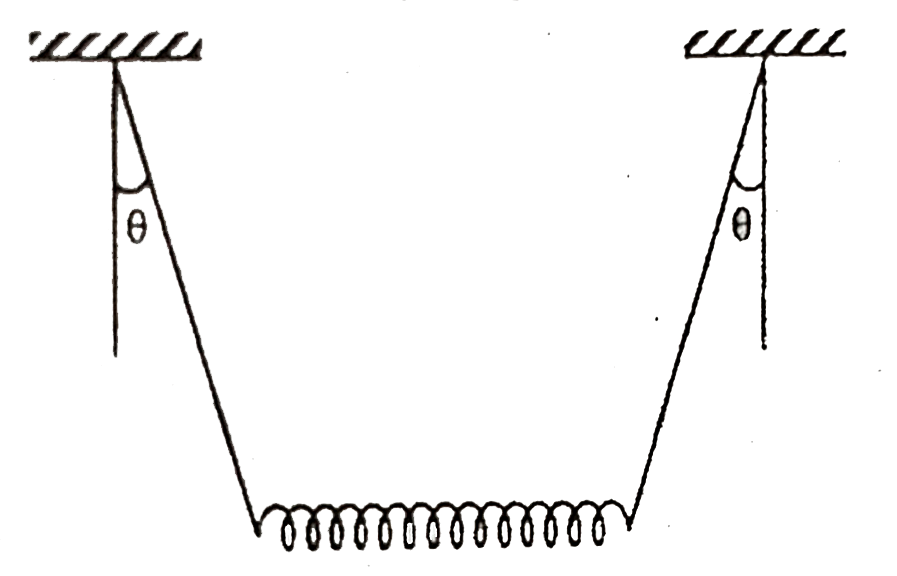
Aspring of weight W and force constant k is suspended in a horizontal position by two light strings attached to its two ends. Each string makes and angle θ with the vertical .The extension of the sporing is
View SolutionA spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.
View Solution
