A uniform disc rotating freely about a vertical axis makes 90 rpm. A small piece of wax of mass m gram falls vertically on the disc and sticks to it at a distance rcm from the axis. If number of rotations per minute reduces to 60, find the moment of inertia of the disc.
To solve the problem, we will use the principle of conservation of angular momentum. Here are the steps to find the moment of inertia of the disc:
Step 1: Understand the initial conditions
The disc is initially rotating at 90 revolutions per minute (rpm). We can convert this to radians per second for calculations:
ωi=90 rpm=90×2π radians1 minute=90×2π60 rad/s=3π rad/s
Step 2: Understand the final conditions
After the wax falls on the disc, the angular velocity reduces to 60 rpm:
ωf=60 rpm=60×2π60 rad/s=2π rad/s
Step 3: Write the conservation of angular momentum equation
According to the conservation of angular momentum:
Li=Lf
Where Li is the initial angular momentum and Lf is the final angular momentum.
The initial angular momentum Li is given by:
Li=Id⋅ωi
Where Id is the moment of inertia of the disc.
The final angular momentum Lf is given by:
Lf=(Id+Iw)⋅ωf
Where Iw is the moment of inertia of the wax.
Step 4: Calculate the moment of inertia of the wax
The moment of inertia of the wax, which is a point mass at a distance r from the axis, is given by:
Iw=m⋅r2
Step 5: Set up the equation
Now we can set up the equation using the conservation of angular momentum:
Id⋅ωi=(Id+m⋅r2)⋅ωf
Step 6: Substitute the values
Substituting the values of ωi and ωf:
Id⋅(3π)=(Id+m⋅r2)⋅(2π)
Step 7: Simplify the equation
Dividing both sides by π:
3Id=2(Id+m⋅r2)
Expanding the right side:
3Id=2Id+2m⋅r2
Step 8: Rearranging the equation
Rearranging gives:
3Id−2Id=2m⋅r2
Id=2m⋅r2
Final Result
Thus, the moment of inertia of the disc is:
Id=2m⋅r2
The disc is initially rotating at 90 revolutions per minute (rpm). We can convert this to radians per second for calculations:
ωi=90 rpm=90×2π radians1 minute=90×2π60 rad/s=3π rad/s
After the wax falls on the disc, the angular velocity reduces to 60 rpm:
ωf=60 rpm=60×2π60 rad/s=2π rad/s
According to the conservation of angular momentum:
Li=Lf
Where Li is the initial angular momentum and Lf is the final angular momentum.
Li=Id⋅ωi
Where Id is the moment of inertia of the disc.
Lf=(Id+Iw)⋅ωf
Where Iw is the moment of inertia of the wax.
The moment of inertia of the wax, which is a point mass at a distance r from the axis, is given by:
Iw=m⋅r2
Now we can set up the equation using the conservation of angular momentum:
Id⋅ωi=(Id+m⋅r2)⋅ωf
Substituting the values of ωi and ωf:
Id⋅(3π)=(Id+m⋅r2)⋅(2π)
Dividing both sides by π:
3Id=2(Id+m⋅r2)
Expanding the right side:
3Id=2Id+2m⋅r2
Rearranging gives:
3Id−2Id=2m⋅r2
Id=2m⋅r2
Thus, the moment of inertia of the disc is:
Id=2m⋅r2
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE B2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE C2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS FOR PRACTICE TYPE A2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
A uniform disc rotating freely about a vertical axis makes 90 revolutions per minute. A small piece of wax of mass m gram falls vertically on the disc and sticks to it at a distance of r cm from the axis. If the number of rotations per minute reduces to 60, find the moment of inertia of the disc.
View SolutionA horizontal disc rotating freely about a vertical axis makes 100 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 9 cm from the axis if the number of revolution per minute is thereby reduced to 90. Calculate the moment of inertia of disc.
View Solution
Knowledge Check
- Question 1 - Select One
The adjoining figure shows a disc of mass M and radius R lying in the X-Y plane with its centre on X - axis at a distance a from the origin. Then the moment of inertia of the disc about the X-axis is
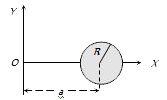 AM(R22)BM(R24)CM(R24+a2)DM(R22+a2)
AM(R22)BM(R24)CM(R24+a2)DM(R22+a2)
A uniform disc is rotating freely about a vertical axis passing through its centre and makes 100 rpm. A small piece of gum of mass 8 g falls vertically on the disc and sticks to it at a distance of 5 cm from its axis. If the number of rotations per minute reduces to 80 rpm find the moment of inertia of the disc.
View SolutionA horizontal disc rotating about a vertical axis makes 100 revolutions per minute. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 9 cm from the axis. If the number of revolutions per minute is thereby reduced to 90, calculate the moment of inertia of disc.
View SolutionA horizontal disc rotating about a vertical axis passing through its centre makes 180 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 8 cm from its axis. If the frequency is thus reduced to 150 rpm, calculate the moment of inertia of the disc.
View SolutionA horizontal disc ratating about a vertical axis passing through its centre makes 180 rpm. A small piece of wax of mass 10g falls vertically on the disc and stricks to it at a distance reduced to 150r±, calculate moment of inertia of the disc.
View SolutionA unifrom horizontal disc is freely rotating about a vertical axis through its centre at the rate of 240 rpm. A blob of wax of mass 2 g falls on it and sticks to it at 25 cm from the axis. If the frequency of rotation of the disc is reduced by 60 rpm. calculate the moment of inertia of the disc. lt
View SolutionA horizontal disc is freely rotating about a vertical axis passing through its centre at the rate of 100r±. A bob of wax of mass 20g falls on the disc and sticks to it a distance of 5cm from the axis. If the moment of inertia of the disc about the given axis is 2×10−4kgm2, find new frequency of rotation of the disc.
View SolutionObtain an expression for potential energy of a particle performing simple harmonic motion. Hence evaluate the potenhtial energy (a) at mean position and (b) extreme position.
A horizontal disc is freely rotating about a transverse axit passing through its centre at the rate of 100 revolutions per minute. A 20 gram blob of wax falls on the disc and sticks to teh disc at a distance of 5 cm form its axis. Moment of inertia of the disc about its axit passing through its centre of mass is 2×10−4 kg m2. Calculate the new frequency of rotation of the disc.View Solution

