The densities of two solid spheres A and B of the same radii R very with radial distance $r a s p_{A} (r) = k (\frac{r}{R}) and p_{B} (r) = k (\frac{r}{{(R)}^{5}},$ respectively, where k is a constant . The moments of inertia of the inividual spheres about axes passing throgh their centres are $I_{A} and I_{B}$ respectively. if $\frac{I_{B}}{I_{A}} = \frac{n}{10},$ the value of n is

A

$6$

B

$10$

C

$16$

D

$7$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let density of sphere of radius x be $ρ (x)$
Here $δ V = 4 π x^{2} . δ x$

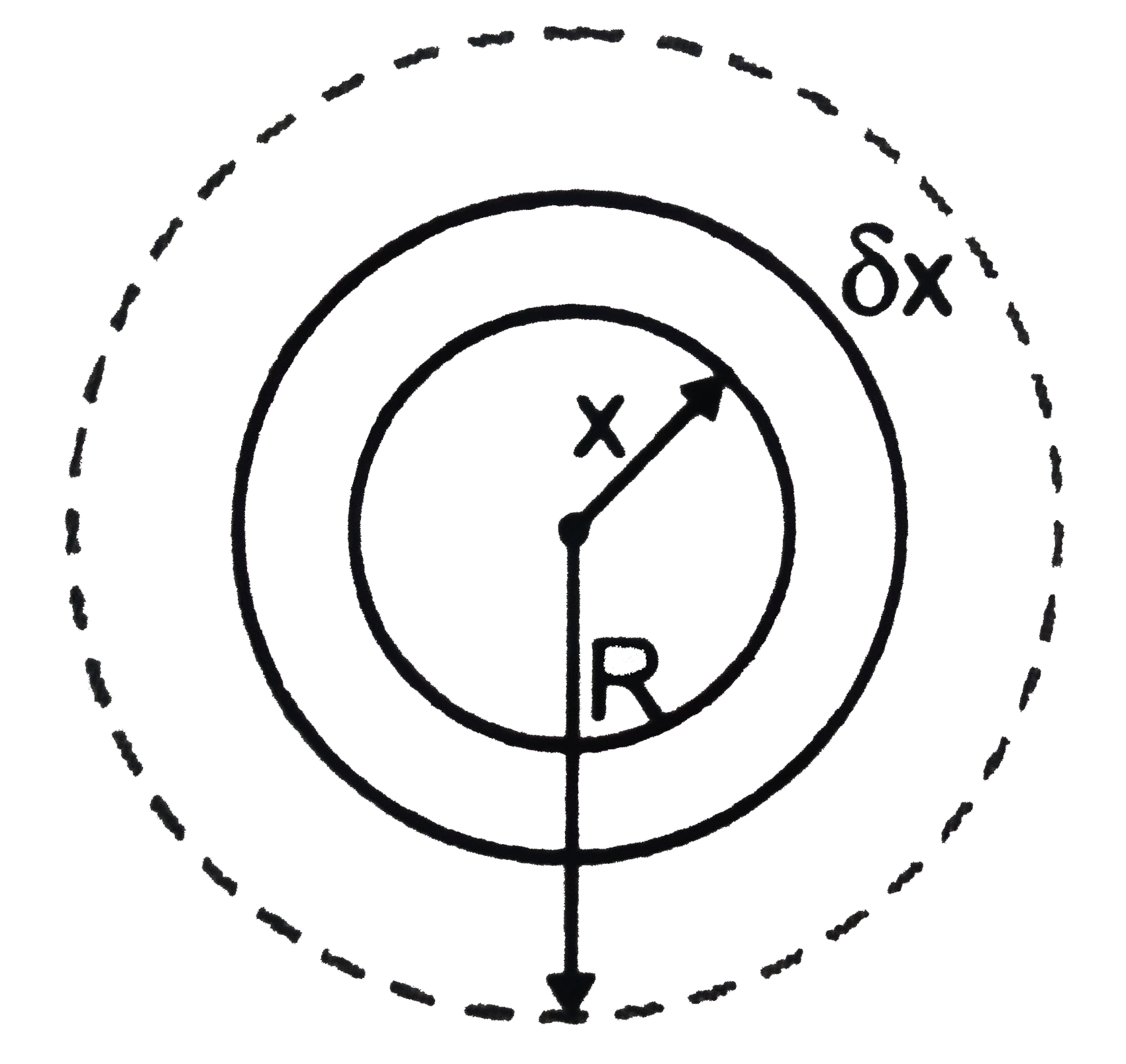
$∴ Δ m = 4 π x^{2} . Δ x . ρ (x)$
Moment of Inertia, $δ I = \frac{2}{3} (δ m) x^{2}$
$= \frac{2}{3} \times 4 π x^{2} δ x ρ (x) . x^{2}$
or $I = \int δ I = R \int 0 \frac{2}{3} 4 π x^{4} δ x . ρ (x)$
or we can say that $I \propto R \int 0 x^{4} δ x . ρ (x)$
Using $ρ_{A} (r) = K (\frac{r}{R})$ and
$ρ_{B} (r) = K {(r / R)}^{5}$ and solving,
we get, $I_{B} / I_{A} = \frac{6}{10} ∴ n = 6$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Knowledge Check

Question 1 - Select One
The moment of inertia of a solid sphere of density p and radius R about its diameter is
A $\frac{176 π R^{3}}{105}$
B $\frac{176 p R^{5}}{105}$
C $\frac{105 p R^{3}}{176}$
D $\frac{105 p R^{5}}{176}$
Question 2 - Select One
Two circular loops A and B of radii R and 2R respectively are made of the similar wire. Their moments of inertia about the axis passing through the centre of perpendicular to their plane are $I_{A} and I_{B}$ respectively. The ratio $\frac{I_{A}}{I_{B}}$ is :
A $\frac{1}{4}$
B $\frac{1}{8}$
C $\frac{1}{2}$
D1
Question 3 - Select One
Moment of inertia of a solid sphere of radius R and density p about its diameter is
A $\frac{176}{105} ρ R^{5}$
B $\frac{176}{105} ρ R^{2}$
C $\frac{105}{176} ρ R^{5}$
D $\frac{105}{176} ρ R^{2}$

Recommended Questions

Home
Ask Doubt
Profile