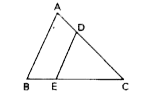
In the figure, $∠ B E D = ∠ B D E$ and E is the middle point of BC. Prove that $\frac{A F}{C F} = \frac{A D}{B E}$

Video Solution

|

Answer

Step by step video & image solution for In the figure, angleBED=angleBDE and E is the middle point of BC. Prove that (AF)/(CF)=(AD)/(BE) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS DEFAULT

Similar Questions

In the figure, $∠ B E D = ∠ B D E$ and E is the middle point of BC. Prove that $\frac{A F}{C F} = \frac{A D}{B E}$
View Solution
In the figure, if $∠ A = ∠ B$ and AD=BE. Prove that CD = CE.

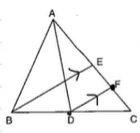
View Solution
In Figure, $A D,$ and $B E$ are medians of $A B C$ and $B E ∣ ∣ D F .$ Prove that $C F = \frac{1}{4} A C .$

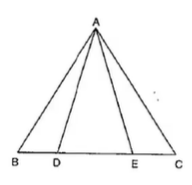
View Solution
In Figure, $A D = A E a n d D a n d E$ are points on $B C$ such that $B D = E C .$ Prove that $A B = A C$

View Solution
Given : AB // DE and BC // EF. Prove that:

$\frac{A D}{D G} = \frac{C F}{F G}$
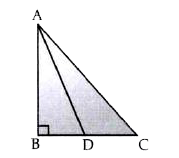
View Solution
In the given figure, triangle ABC is a right triangle with $∠ B = 90^{\circ} and D$ is mid-point of side BC. Prove that :
$A C^{2} = A D^{2} + 3 C D^{2}$

View Solution
In the given figure ABC is a right angled triangle with $∠ B = 90^{\circ}$ . D is the mid -point of BC . Show that $A C^{2} = A D^{2} + 3 C D^{2}$ .

View Solution
AD,BE and CF are the medians of a $Δ A B C$ . Prove that $2 (A D + B E + C F) < 3 (A B + B C + C A) < 4 (A D + B E + C F)$
View Solution
If the diagonal BD of a quadrillateral ABCD bisects both $∠ B and ∠ D$ . Prove that $\frac{A B}{B C} = \frac{A D}{C D}$ .
View Solution
If the diagonal BD of a quadrillateral ABCD bisects both $∠ B and ∠ D$ . Prove that $\frac{A B}{B C} = \frac{A D}{C D}$ .
View Solution

In the figure, ∠BED=∠BDE and E is the middle point of BC. Prove that AFCF=ADBE

Similar Questions

Recommended Questions

In the figure, $∠ B E D = ∠ B D E$ and E is the middle point of BC. Prove that $\frac{A F}{C F} = \frac{A D}{B E}$