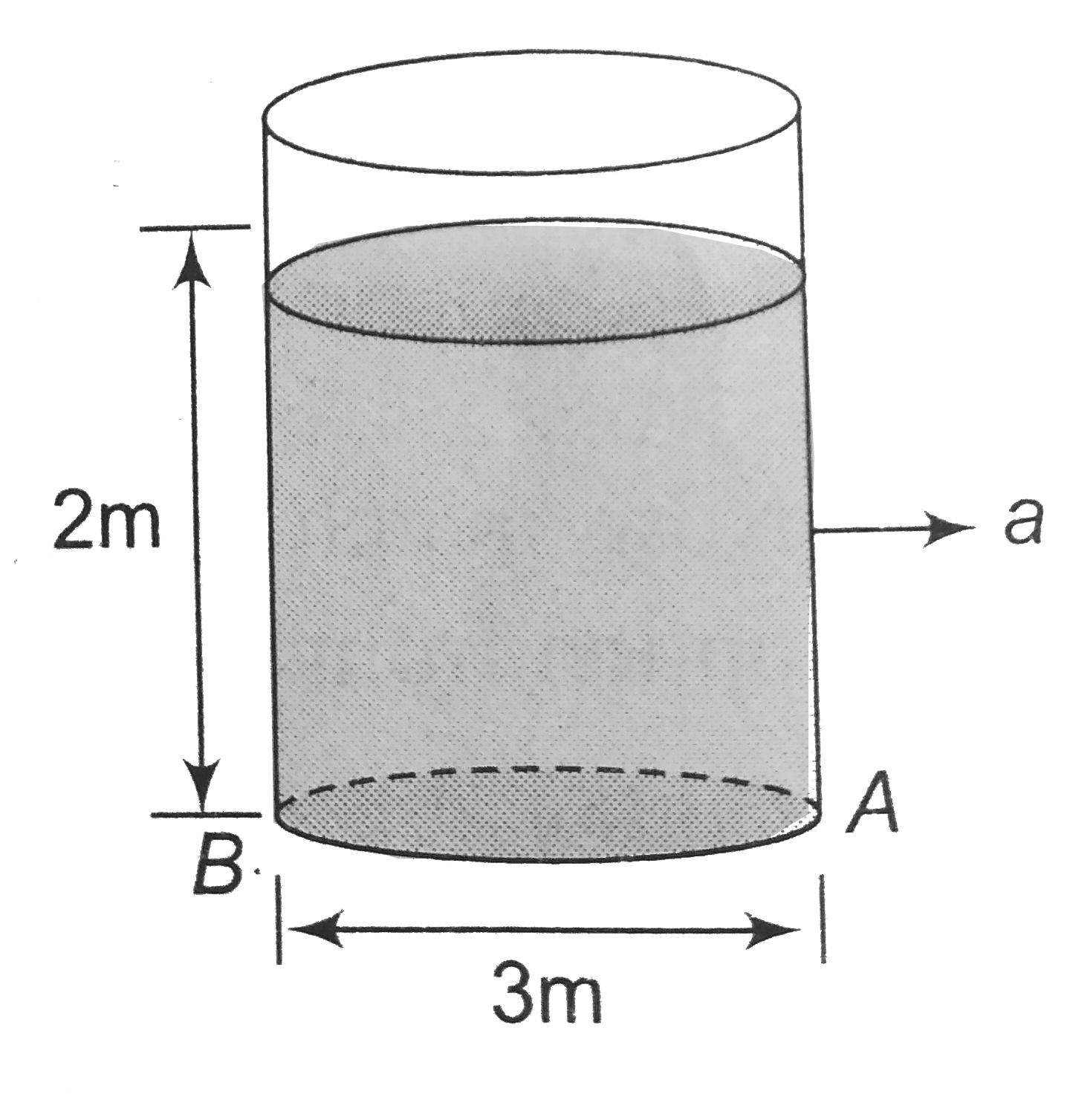
The minimum horizontal acceleration of the container IS a so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)
32g
43g
42g
34g
The correct Answer is:B
(b) Volume equality gives

2×3=12×h×3⇒h=4m
∴tanθ=43=ag⇒a=43g
Topper's Solved these Questions
- FLUID MECHANICSBOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Buoyancy And Floatation
40 Videos
- FLUID MECHANICSBOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Continuity Equation And Bernoulli'S Theorem
32 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
The minimum horizontal acceleration of the container IS a so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)
 A32gB43gC42gD34g
A32gB43gC42gD34gThe pressure at the bottom of a tank containing a liquid does not depend on
AAcceleration due to gravityBHeight of the liquid columnCArea of the bottom surfaceDNature of the liquidThe pressure at the bottom of a tank containing a liquid does not depend on
AAcceleration due to gravityBHeight of the liquid columnCArea of the bottom surfaceDNature of the liquid
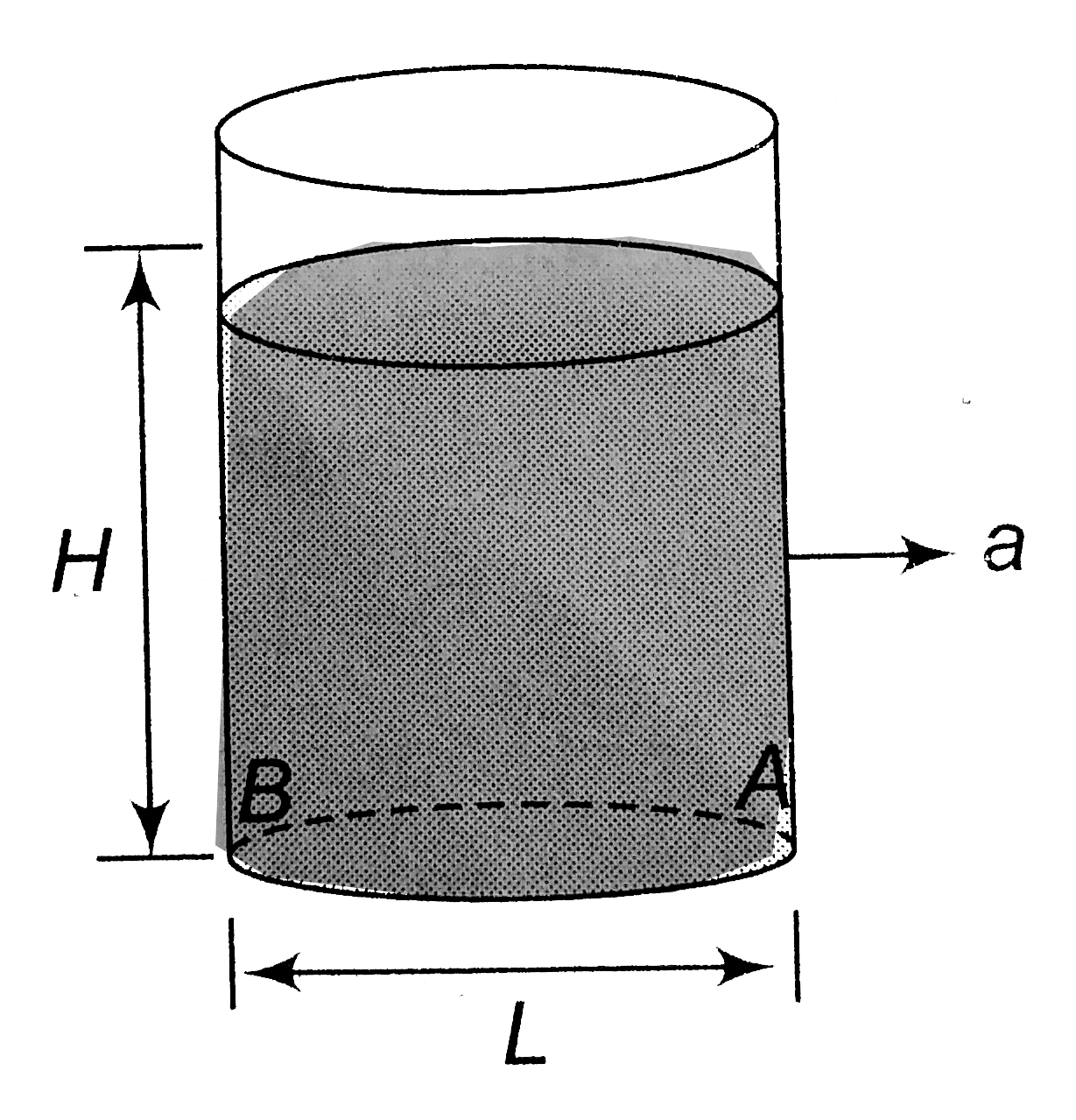
Figure shows an L-shaped tube tilled with a liquid to a height H. What should be the horizontal acceleration a of the tube so that the pressure at the point A becomes atmospheric.

View SolutionA tank with base area L2 is filled with a liquid to height H. The tank is acceleration horizontally with acceleration a as shown in figure. If a small hole is made at the point A. then it is observed that the liquid does not come out of the tank. The magnitude of acceleration should be
View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)

View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure =105N/m2 density of water =1000kg/m3,g=10m/s2)
View SolutionIf the pressure at half the depth of a tank is equal to 23 the pressure at the bottom of the tank, then the height of the water column in the tank is
(Atmospheric pressure =105N/m2)
View Solution
