To get the maximum flight a ball must be thrown as :

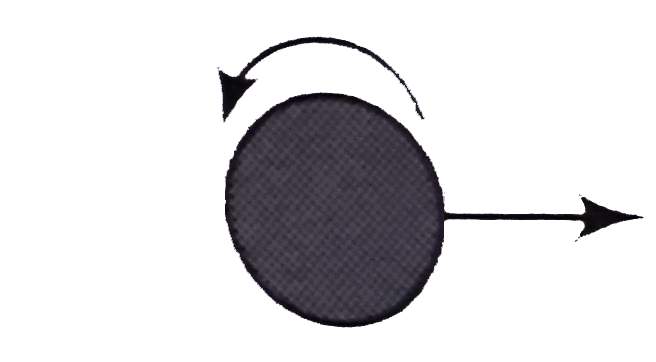


The correct Answer is:B
To determine how to achieve maximum flight for a ball when thrown, we can analyze the effects of velocity and spin on the ball's trajectory using Bernoulli's principle. Here’s a step-by-step solution:
Step 1: Understand the Concept of Bernoulli's Principle
Bernoulli's principle states that in a fluid flow, an increase in the fluid's velocity occurs simultaneously with a decrease in pressure. This principle will help us analyze the effects of different throwing techniques on the ball's flight.
Hint: Recall that Bernoulli's equation relates pressure and velocity in fluid dynamics.
Step 2: Analyze the Options Given
We have four options regarding how to throw the ball:
1. Forward velocity with clockwise spin.
2. Forward velocity with anti-clockwise spin.
3. Only forward velocity.
4. Any of these methods could yield the same result.
Hint: Consider how the direction of spin affects the velocity distribution around the ball.
Step 3: Evaluate Option A (Clockwise Spin)
When the ball is thrown with a forward velocity and a clockwise spin:
- The upper surface of the ball has a velocity of V−Rω (where R is the radius and ω is the angular velocity).
- The lower surface has a velocity of V+Rω.
- This results in higher pressure on the top and lower pressure on the bottom, creating a net downward force.
Hint: Think about how the pressure differences affect the ball's flight.
Step 4: Evaluate Option B (Anti-clockwise Spin)
When the ball is thrown with a forward velocity and an anti-clockwise spin:
- The upper surface has a velocity of V+Rω.
- The lower surface has a velocity of V−Rω.
- This results in lower pressure on the top and higher pressure on the bottom, creating a net upward force.
Hint: Consider how the upward force could enhance the ball's flight.
Step 5: Evaluate Option C (Only Forward Velocity)
If the ball is thrown with only forward velocity, there are no pressure differences created by spin. The pressures above and below the ball remain equal, resulting in no net force acting on the ball.
Hint: Reflect on how the absence of spin affects the pressure distribution.
Step 6: Conclusion
From the analysis:
- Option A results in a net downward force, reducing flight.
- Option B results in a net upward force, enhancing flight.
- Option C provides no net force.
Thus, the best method to achieve maximum flight for the ball is to throw it with a forward velocity and an anti-clockwise spin (Option B).
Final Answer: To achieve maximum flight, the ball must be thrown with a forward velocity and an anti-clockwise spin (Option B).
Bernoulli's principle states that in a fluid flow, an increase in the fluid's velocity occurs simultaneously with a decrease in pressure. This principle will help us analyze the effects of different throwing techniques on the ball's flight.
We have four options regarding how to throw the ball:
1. Forward velocity with clockwise spin.
2. Forward velocity with anti-clockwise spin.
3. Only forward velocity.
4. Any of these methods could yield the same result.
When the ball is thrown with a forward velocity and a clockwise spin:
- The upper surface of the ball has a velocity of V−Rω (where R is the radius and ω is the angular velocity).
- The lower surface has a velocity of V+Rω.
- This results in higher pressure on the top and lower pressure on the bottom, creating a net downward force.
When the ball is thrown with a forward velocity and an anti-clockwise spin:
- The upper surface has a velocity of V+Rω.
- The lower surface has a velocity of V−Rω.
- This results in lower pressure on the top and higher pressure on the bottom, creating a net upward force.
If the ball is thrown with only forward velocity, there are no pressure differences created by spin. The pressures above and below the ball remain equal, resulting in no net force acting on the ball.
From the analysis:
- Option A results in a net downward force, reducing flight.
- Option B results in a net upward force, enhancing flight.
- Option C provides no net force.
Topper's Solved these Questions
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Application Of Bernoulli'S Theorem And Velocity Of Efflux
Explore 19 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Problems Based On Mixed Concepts
Explore 29 Videos
- FLUID MECHANICSBook:A2ZChapter:FLUID MECHANICSExercise:Buoyancy And Floatation
Explore 40 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBook:A2ZChapter:GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONExercise:Chapter Test
Explore 30 Videos
Similar Questions
A ball is thrown from the ground with velocity u at an angle θ with horizontal. If the coefficient of restitution is e , find the time of flight , the maximum height and the horizontal range after the first collision.
View SolutionA boy throws a ball at an angle θ with the vertical. If the vertical component of the initial velocity is 20ms−1 and the wind imparts a horizontal acceleration of 8ms−2 to the left, the angle at which the ball must be thrown so that the ball returns to the boy's hand is θ. What is the value of 10(tanθ)
View Solution
Knowledge Check
When a ball is thrown up vertically with velocity v0, it reaches a maximum height of h. If one wishes to triple the maximum height then the ball should be thrown with velocity
A√3v0B3v0C9v0D32v0Get the ball rolling
ATo spin the ballBTo cheer someone upCTo have an active lifestyleDTo start doing somethingBalls are thrown vertically upwards in such a way that the next ball is thorwn when the previous one is at the maximum height. If the maximum hieght is 5m, the number of balls thrown per minute will be
A40B50C60D120
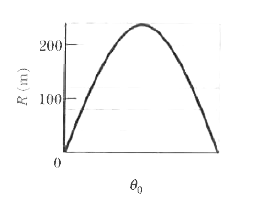
A ball is to be shot from level ground with a certain speed. Figure 4-38 shows the range R it will have versus the launch angle θ0. The value of θ0 determines the flight time, let tmax represent the maximum flight time. What is the least speed the ball will have during its flight if θ0 is chosen such that the flight time is 0.500tmax?
View SolutionIn quick succession, a large number of balls are throun up vertically in such a way that the next ball is thrown up when the previous ball is at the maximum height. If the maximum height is 5m, then find the mumber of the thrown up per second (g=10 m s^(-2)).
View SolutionA small ball of mass m is thrown upward with velocity u from the ground. The ball experiences a resistive force mkv2 where v is its speed. The maximum height attained by the ball is :
View SolutionA very large number of balls are thrown vertically upwards in quick successions in such a way that the next ball is thrown when the previous one is at the maximum height. If the maximum height is 5m, then number of balls thrown per minute is (take g=10m/s2)
View SolutionTwo balls are thrown with the same speed from a point O at the same time so that their horizontal ranges are same. If the difference of the maximum height attained by them is equal to half of the sum of the maximum heights, then the angles of projection for the balls are
View Solution