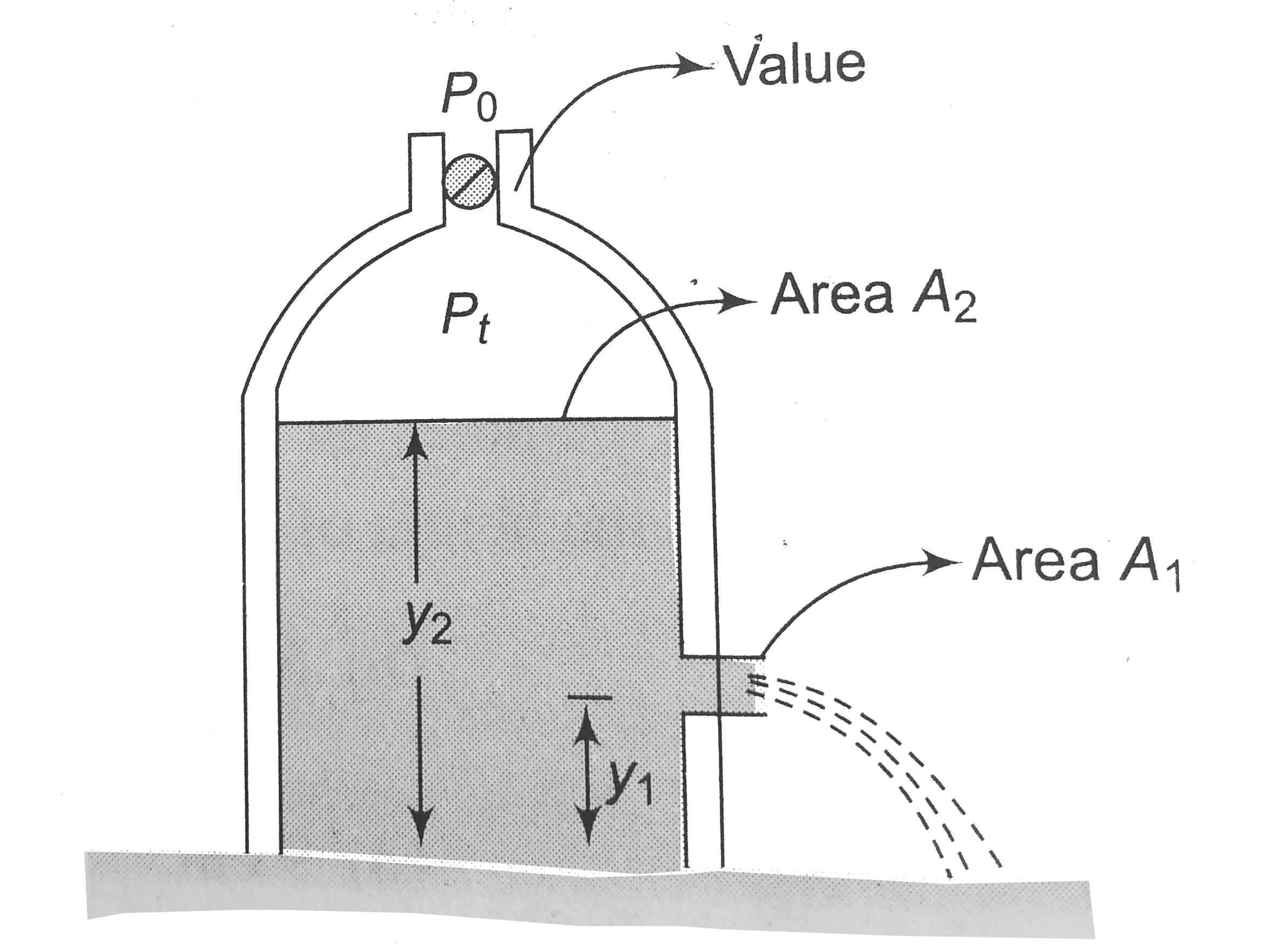
A tank has a small hole on its side at a height $y_{1}$ . It is filled with a liquid (density $ρ$ ) to a height $y_{2}$ . If the absolute pressure at the top of the fluid is $P_{t}$ , find the velocity with which it leaves the tank. Assume that the cross-sectional area of the tank is larger as compared to that of the hole.

$\sqrt{\frac{2 (P_{t} - P_{0})}{ρ} + 2 g (y_{2} - y_{1})}$

$\sqrt{\frac{P_{t} - P_{0}}{ρ} + 2 g (y_{2} - y_{1})}$

$\sqrt{\frac{P_{t} - P_{0}}{ρ} - 2 g (y_{2} - y_{1})}$

$\sqrt{\frac{2 P_{t}}{ρ} + 2 g (y_{2} - y_{1})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

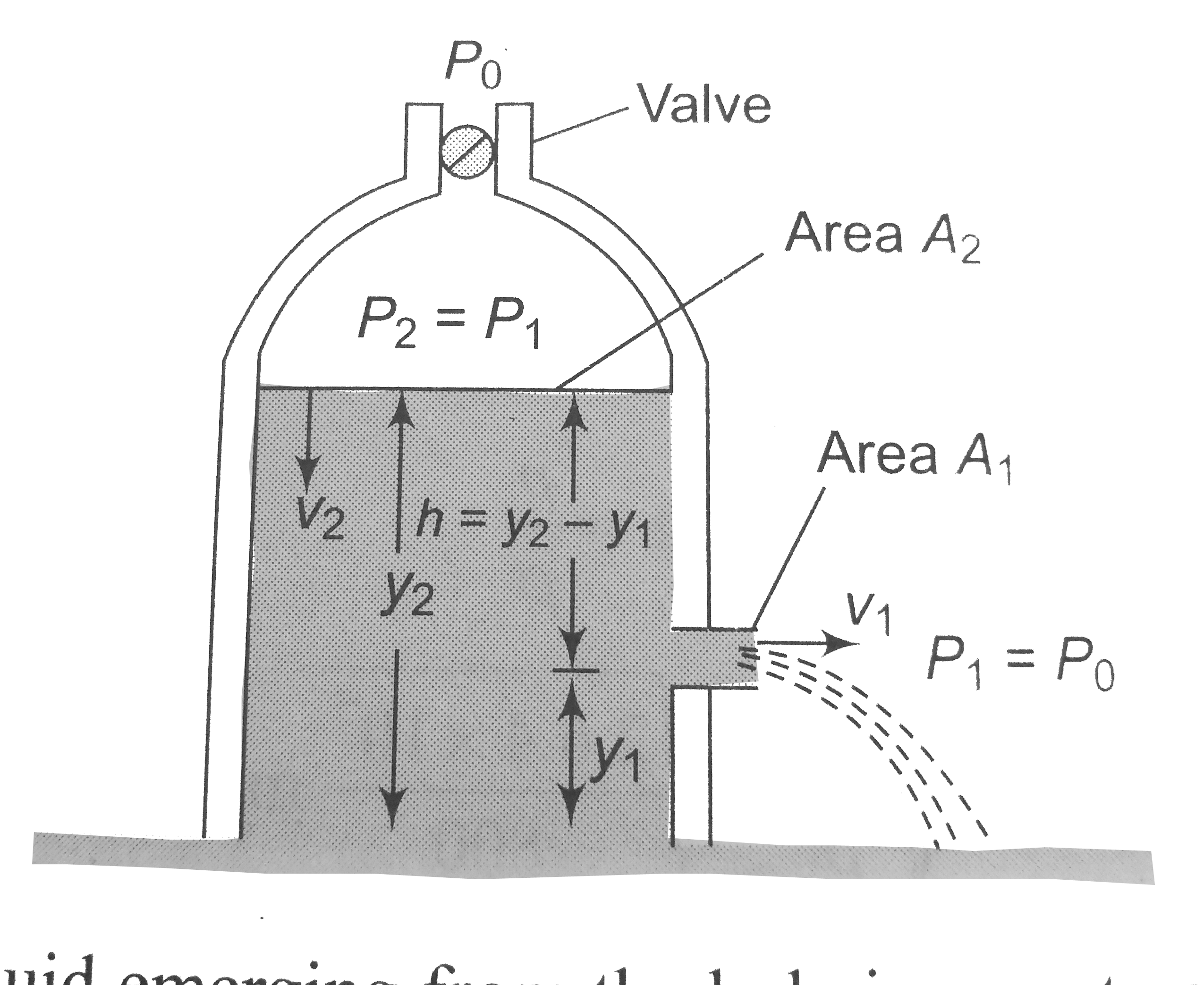
From equation of continuity, $v_{2} = \frac{A_{1}}{A_{2}} v_{1}$
Since $A_{1} < < A_{2}, v_{2}$ must be very small compared to velocity of efflux at the hole, therefore we can take $v_{2} = 0$
Fluid emerging form the holes is open to atmosphereic pressure $P_{0}$ . we take two points $A$ and $B$ at the top of the fluid and at the hole respectively. From Bernoulli's principle,
$P_{0} + \frac{1}{2} ρ v_{1}^{2} + ρ g y_{1} = P_{1} + ρ g y_{2}$
Solving for $v_{1}$ , we obtain $v_{1} = \sqrt{\frac{2 (p_{t} - p_{0})}{ρ}} + 2 g h$ .

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A tank has a small hole on its side at a height $y_{1}$ . It is filled with a liquid (density $ρ$ ) to a height $y_{2}$ . If the absolute pressure at the top of the fluid is $P_{t}$ , find the velocity with which it leaves the tank. Assume that the cross-sectional area of the tank is larger as compared to that of the hole.

A $\sqrt{\frac{2 (P_{t} - P_{0})}{ρ} + 2 g (y_{2} - y_{1})}$
B $\sqrt{\frac{P_{t} - P_{0}}{ρ} + 2 g (y_{2} - y_{1})}$
C $\sqrt{\frac{P_{t} - P_{0}}{ρ} - 2 g (y_{2} - y_{1})}$
D $\sqrt{\frac{2 P_{t}}{ρ} + 2 g (y_{2} - y_{1})}$
Question 2 - Select One
A hole is made at the bottom of the tank filled with water (density $= 1000 k g m^{- 3})$ . If the total pressure at the bottom of the tank is three atmospheres (1 atmosphere $= 10^{5} N m^{- 2})$ , then the velocity of efflux is nearest to
A $\sqrt{400} m s^{- 1}$
B $\sqrt{200} m s^{- 1}$
C $\sqrt{600} m s^{- 1}$
D $\sqrt{500} m s^{- 1}$
Question 3 - Select One
A cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density $ρ / 3$ .

Situation I: Initially, the tank is filled with water of density $ρ$ to a height such that the height of water above the top of the block is $h_{1}$ (measured from the top of the block).
Situation II: The water is removed from the tank to a height $h_{2}$ (measured from the bottom of the block), as shown in the figure. The height $h_{2}$ is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the minimum value of height $h_{1}$ (in situation 1), for which the block just starts to move up?
A(a) $\frac{2 h}{3}$
B(b) $\frac{5 h}{4}$
C(c) $\frac{5 h}{3}$
D(d) $\frac{5 h}{2}$

A2Z-FLUID MECHANICS-Application Of Bernoulli'S Theorem And Velocity Of Efflux

Home
Ask Doubt
Profile

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

A hole is made at the bottom of the tank filled with water (density =1000kgm−3). If the total pressure at the bottom of the tank is three atmospheres (1 atmosphere =105Nm−2), then the velocity of efflux is nearest to

A2Z-FLUID MECHANICS-Application Of Bernoulli'S Theorem And Velocity Of Efflux

A hole is made at the bottom of the tank filled with water (density $= 1000 k g m^{- 3})$ . If the total pressure at the bottom of the tank is three atmospheres (1 atmosphere $= 10^{5} N m^{- 2})$ , then the velocity of efflux is nearest to