A candle of diameter d is floating on a liquid in a cylindrical container of diameter D(D<<d) as shown in figure. If it is burning at the rate of 2cm/h then the top of the candle will :
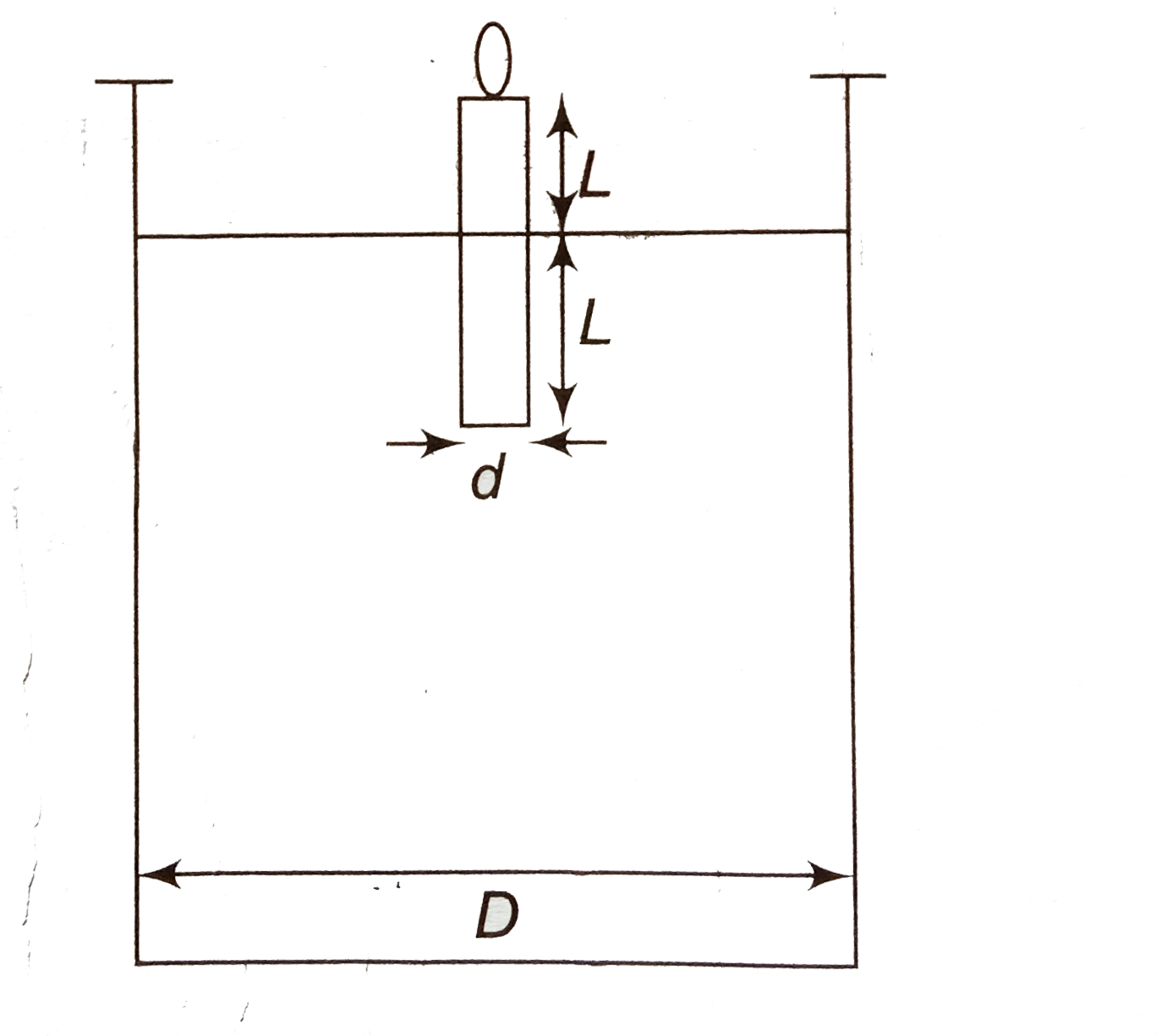
remains uchanged
fall at the rate of 1cm/hour
fall at the rate of 2cm/hour
go up the rate of 1cm/hour
The correct Answer is:B
From Archimedes' principle this apparent loss in weight is equal to the weight of the liquid displaced by the body.
Also volume of candle =Area×≤n>h
=π(d2)2×2L
Weight of candle = Weight of liquid displaced
Vρg=V'ρ'g'
⇒(πd24×2L)ρ=(πd24×L)ρ'
⇒ρρ'=12
Since candle is burning at the rate of 2cm/h, then after an hour, candle length is 2L−2
∴(2L−2)ρ=(L−x)ρ'
.ρρ'=L−x2(L−1)
12=L−x2(L−1)
⇒x=1cm
Hence in one hour it melts 1 cm and so it falls at the rate of 1cm/h.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - Chapter Test
29 Videos
- FLUID MECHANICSBOOK - A2ZCHAPTER - FLUID MECHANICSEXERCISE - NEET Questions
7 Videos
- GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONBOOK - A2ZCHAPTER - GENERAL KINEMATICS AND MOTION IN ONE DIMENSIONEXERCISE - Chapter Test
30 Videos
Similar Questions
The inner diameter ofa cylindrical container is 7 cm and its top is of the shape of a hemisphere, as shown in the figure. If the height of the container is 16 cm, find the actual capacity of the container.
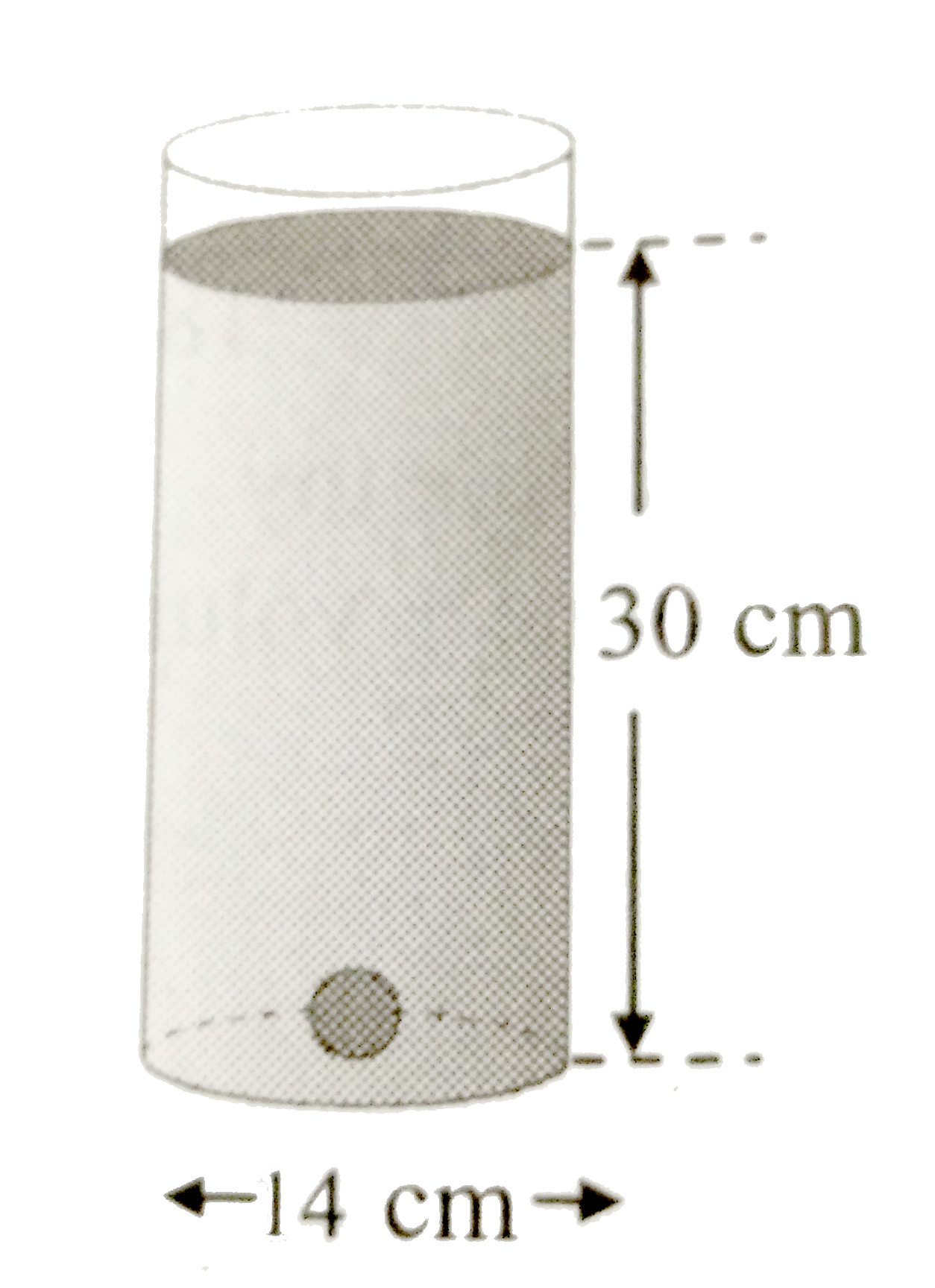
View SolutionAs shown in the figure, a cylindrical glass contains water. A metal sphere of diameter 2 cm is immersed in it. Find the volume of the water.
View Solution
Knowledge Check
A candle of diameter d is floating on a liquid in a cylindrical container of diameter D(D<<d) as shown in figure. If is burning at the rate of 2cm/h then the top of the candle will :
 Aremain at the same heightBfall at the rate of 1cm/hCfall at the rate of 2cm/hDgo up at the rate of 1cm/h
Aremain at the same heightBfall at the rate of 1cm/hCfall at the rate of 2cm/hDgo up at the rate of 1cm/hA metallic sphere of diameter D has a cavity of diameter d at its centre. If the sphere is heated, the diameter of the cavity will:
ADecreaseBIncreaseCRemain unchangedDDecrease if d<D/2 and increase if d>D/2A beam of diameter 'd' is incident on a glass hemisphere as shown in the figure. If the radius of curvature of the hemisphere is very large in comparision to d, then the diameter of the beam at the base of the hemisphere will be:
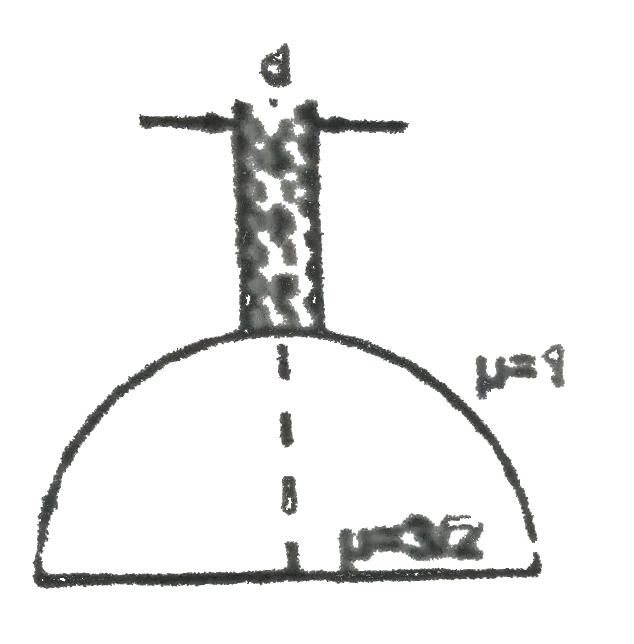 A34dBdCd3D23d
A34dBdCd3D23d
As shown in the figure, a cylindrical glass contains water. A metal sphere of diameter 2 cm is immersed in it . Find the volume of the water.

View SolutionA cylindrical hall of diameter D and height h is illuminated by a lamp fixed at the centre of the celing. Compare the minimum illumination of the froor.
View SolutionA hemispherical bowl of internal radius 12 cm contains liquid. This liquid is to be filled into cylindrical container of diameter 4 cm and height 3 cm. The number containers that is necessary to empty the bowl is (a) 80 (b) 96 (c) 100 (d) 112
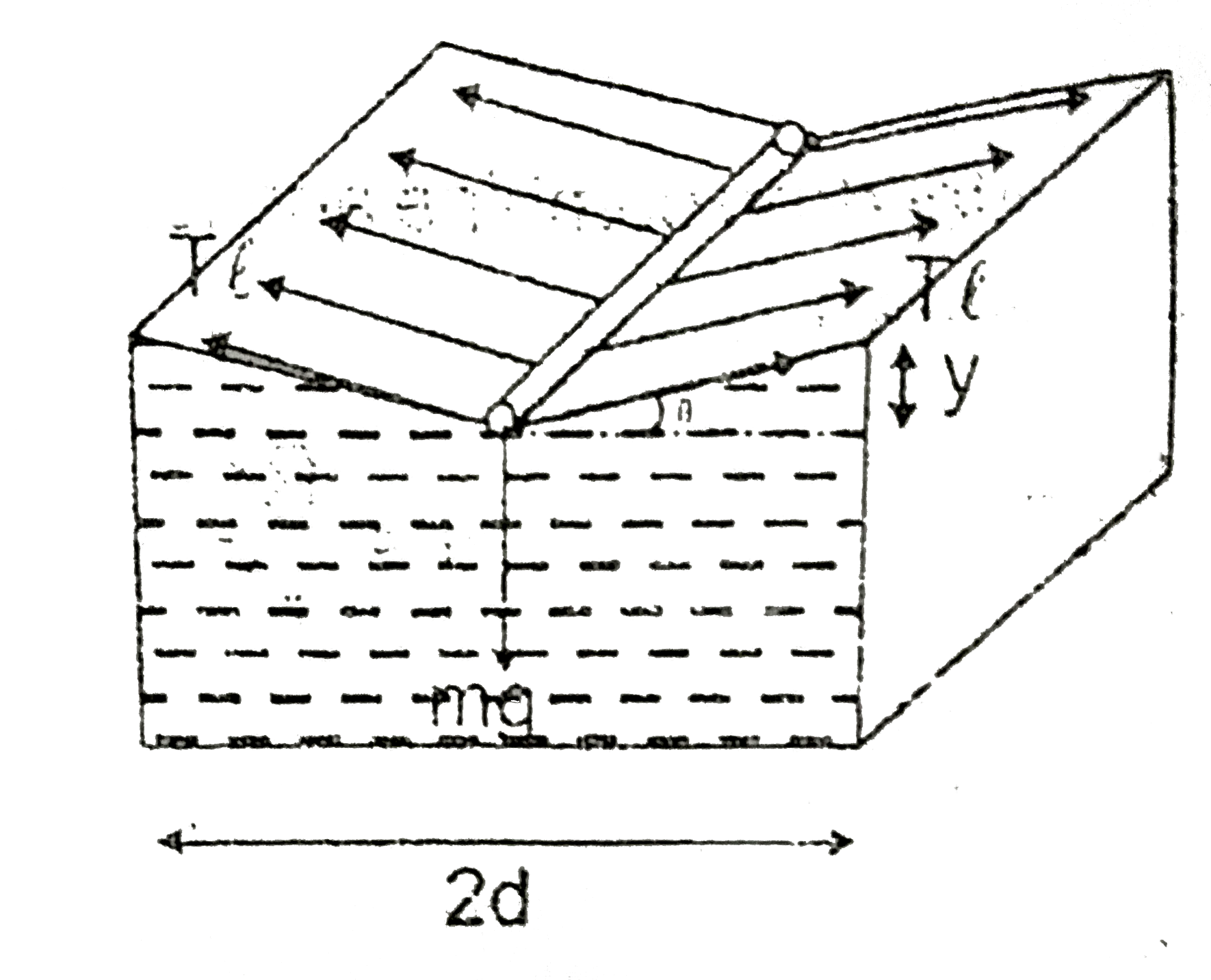
View SolutionA long thin straight uniform wire of negligible radius is supported on the surface of a liquid. The width of the container is 2d and the wire is kept at its centre, parallel to its length (as shown in figure). The surface of the liquid is depressed by a veritcal distance y(y<<d) at the centre as shown in figure. If the wire has mass λ per unit length, what is the surface tension of the liquid? igonre end effects.
View SolutionWhen a body of density d1 and volume V is floating in a liquid of density d2
View Solution
