In the figure shown , A and B are free of to move. All the surfaces are smooth. (0<θ<90∘)

the acceleration of A will be more than gsinθ
the acceleration of A will be less than gsinθ
normal force on A due to B will be more than mgcosθ
normal force on A due to B will be less than mgcosθ
The correct Answer is:A::D
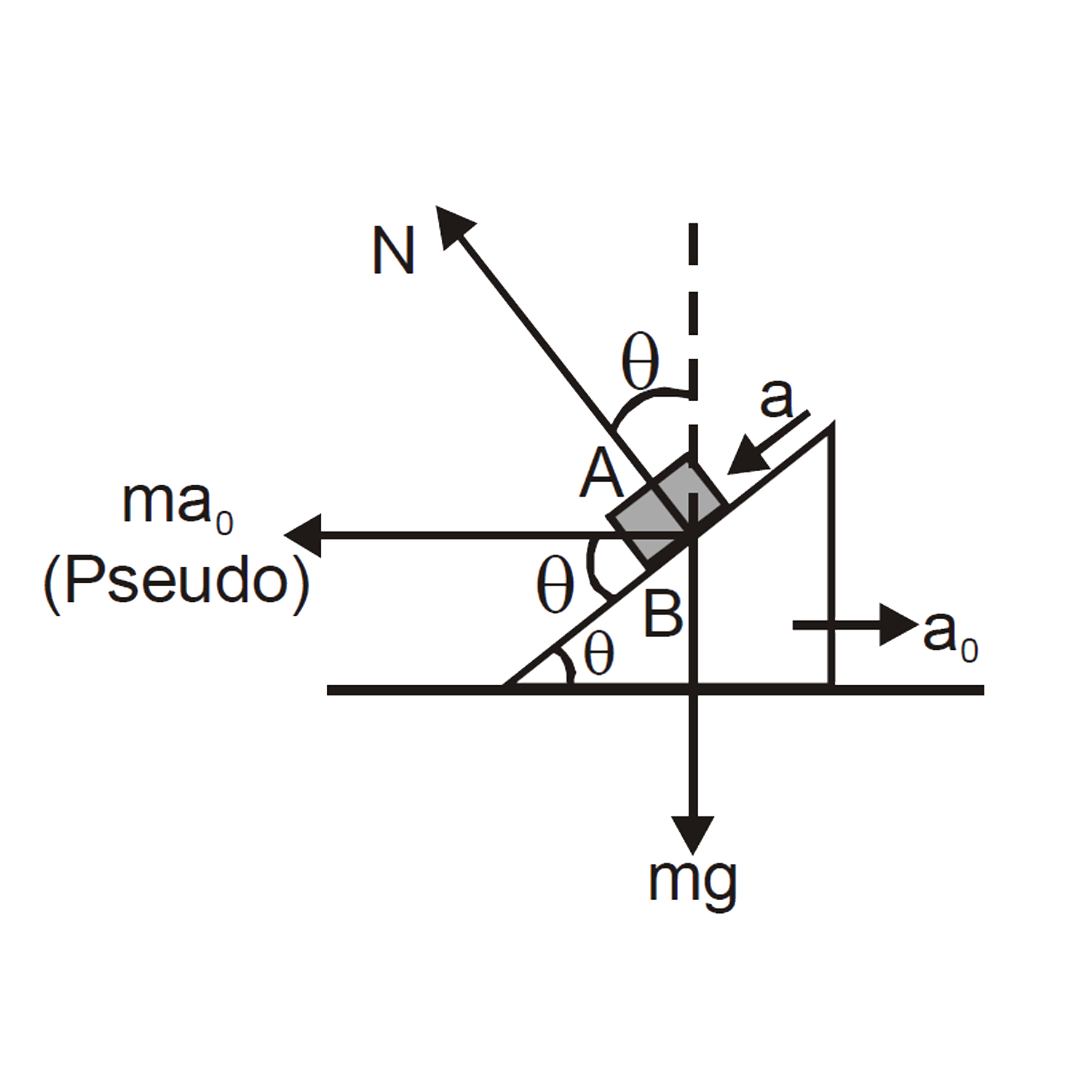
ma0sinθ+N=mgcosθ⇒N=mgcosθ=ma0sinθ
⇒N<mgcosθ
Hence, (D) is ture.
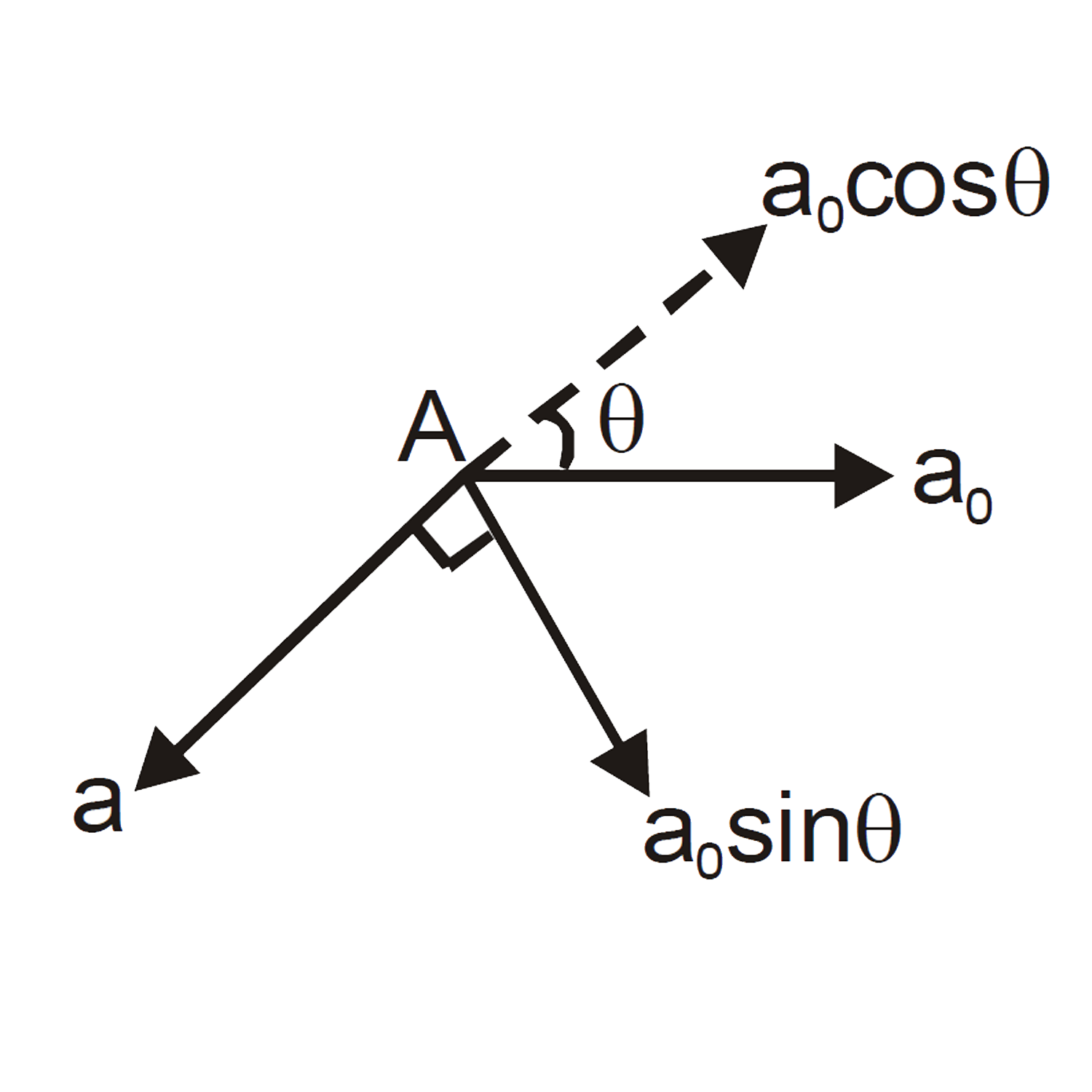
ma0cosθ+mgsinθ=ma
⇒a=gsinθ+a0cosθ
Hence acceleration of A
=√(a−a0cosθ)2+(a0sinθ)2>gsinθ
Topper's Solved these Questions
Similar Questions
A particle is moving along a circle with a uniform speed v. Find (a) change in the magnitude of velocity and (b) the magnitude of change in the velocity when it has rotated an angle θ.(0<θ<90∘)
View SolutionIn the shown figure, if all the surface are smooth and the two masses are allowed to move then center of mass of the system will move
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
In the figure shown A and B are free to move . All the surface are smooth. Mass of Aism. Then
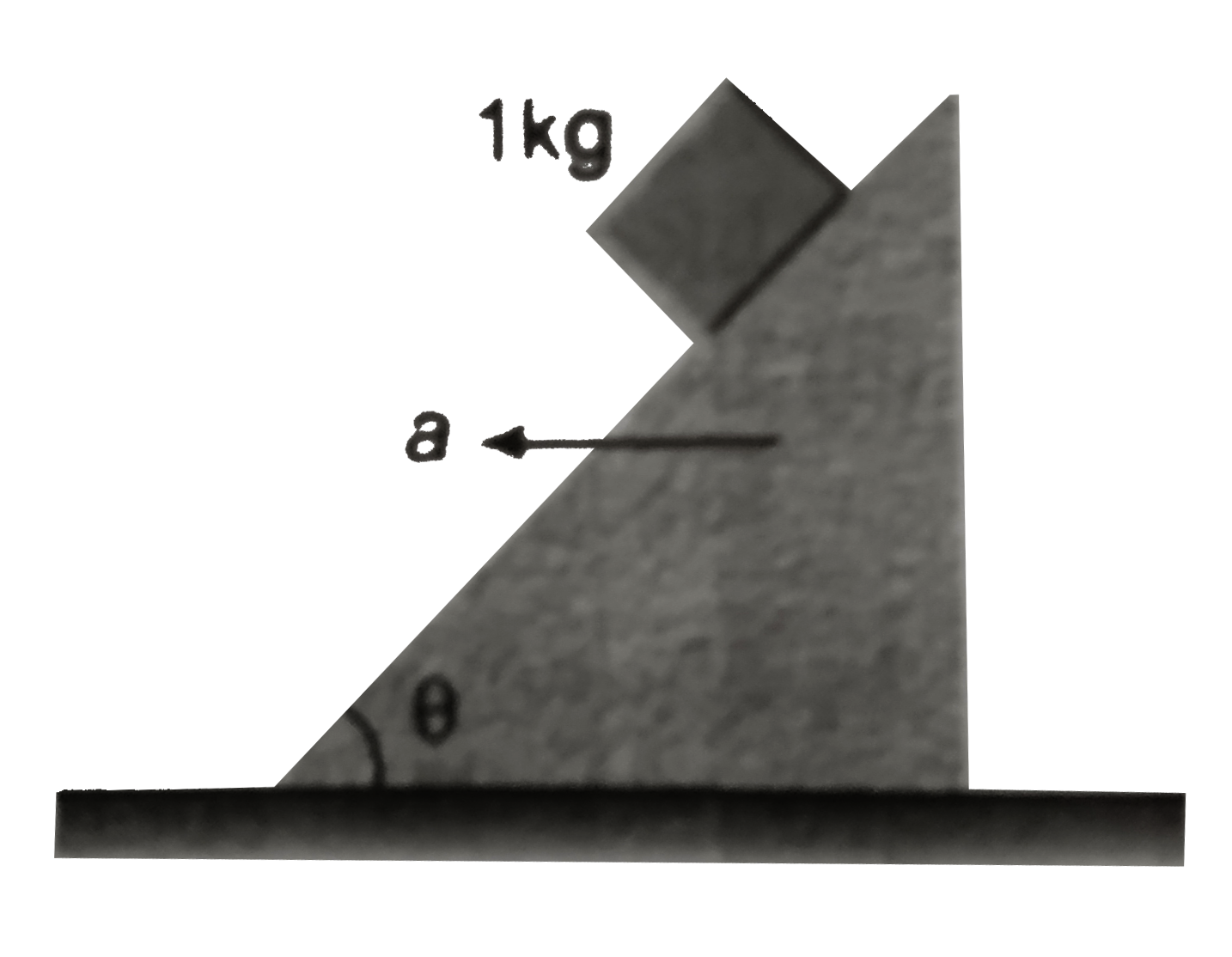 Athe acceleration of A will be more than gsinθBthe acceleration of A will be less than gsinθCnormal reation A due to B will be more than mgcosθDnormal reation A due to B will be less than mgcosθ
Athe acceleration of A will be more than gsinθBthe acceleration of A will be less than gsinθCnormal reation A due to B will be more than mgcosθDnormal reation A due to B will be less than mgcosθ - Question 2 - Select One
Which of the following relations is correct for 0<θ<90∘ ?
Asinθ=sin2θBsinθ<sin2θCsinθ>sin2θDsinθ=sosec2θ - Question 3 - Select One
The reflecting surface of two intersecting flat mirrors are at an angle θ(0∘<θ<90∘). As shown in Figure. For a light ray that strikes the horizontal mirror, the emerging ray intersects the incident ray at an angle β . If one of the mirrors is rotated at dθdt=1∘/s, then the angle β changes aat the rate of
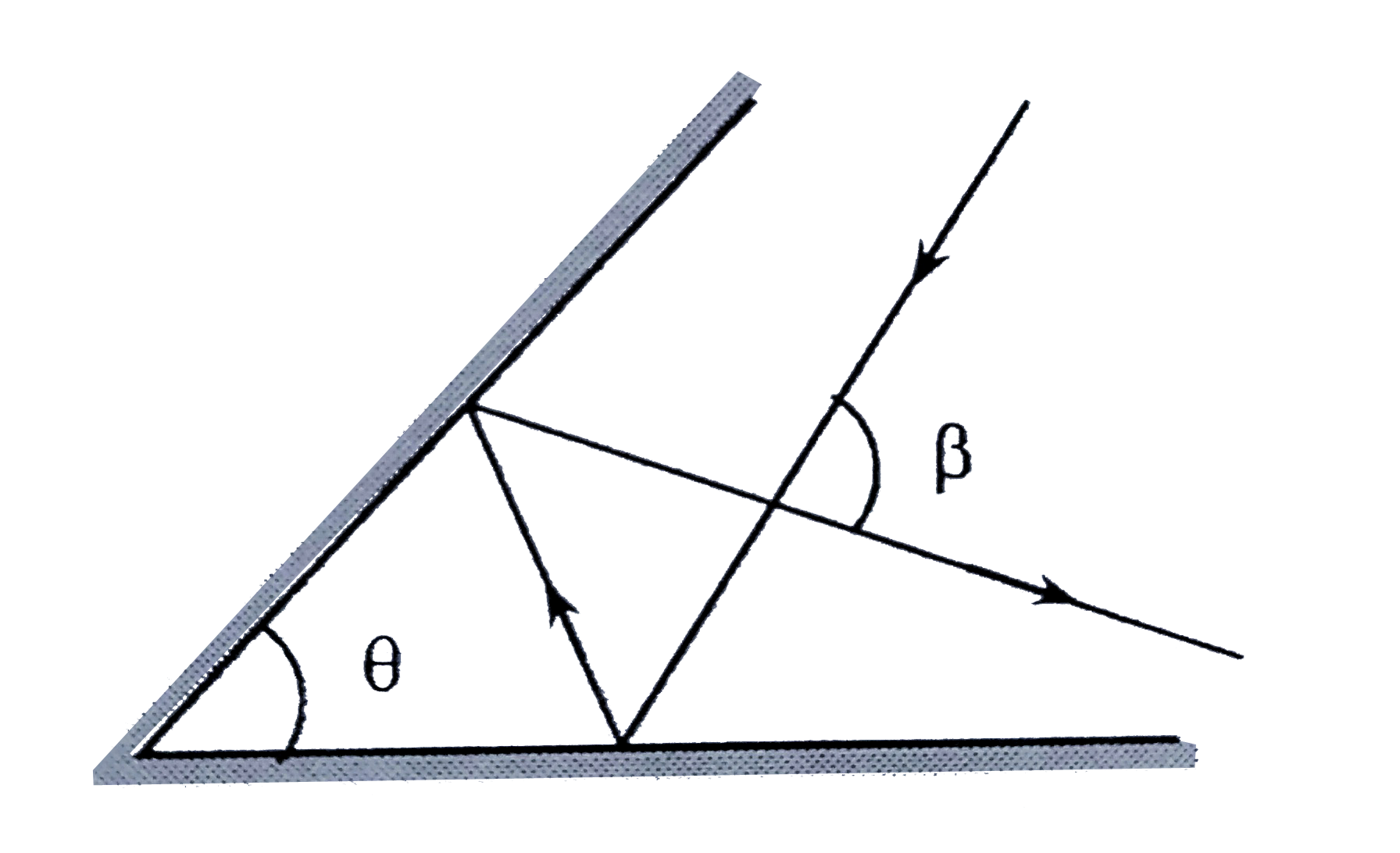 A1∘/sB2∘/sC−1∘/sD−2∘/s
A1∘/sB2∘/sC−1∘/sD−2∘/s
Describe the path of a charged particle moving in a uniform magnetic field with initial velocity
(i) parallel to (or along) the field.
(ii) perpendicular to the field.
(iii) at an arbitrary angle θ(0∘<θ<90∘).View SolutionIf cosθ1−sinθ+cosθ1+sinθ=4, then find the value of cosθ. Find θ if 0∘<θ<90∘
View SolutionIn the previous problem ,find the magnitude of change in velocity if (a) 90∘<θ<180∘ , (b) 180∘<θ<270∘ and (c ) 270∘<θ<360∘.
View SolutionFor what value of θ, is (tanθ+cosecθ)=2.5 where 0<θ≤90∘ ?
View SolutionIf the angle (θ) between velocity vector and the acceleration vector of a moving particle is 90∘<θ<180∘, then the path of the particle is
View Solution

