AB wire (length x) is vibrating in its fundamental mode. Wire AB is in resonance with resonance tube in which air column (length x/2) is also vibrating with its fundamental mode. Sound speed is 400 m/sec and linear mass density of AB wire is 10−4 kg/m and g=10 m/sec2, value of mass m =[β(10−1)]kg, then find value of β.Neglect the masses of wires in comparison to block's mass 'm'.
![AB wire (length x) is vibrating in its fundamental mode. Wire AB is in resonance with resonance tube in which air column (length x/2) is also vibrating with its fundamental mode. Sound speed is 400 m/sec and linear mass density of AB wire is 10^-4 kg/m and g=10 m//sec^2, value of mass m =[beta(10^-1)] kg, then find value of beta.Neglect the masses of wires in comparison to block's mass 'm'.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_DPP_PHY_09_E01_028_Q01.png)
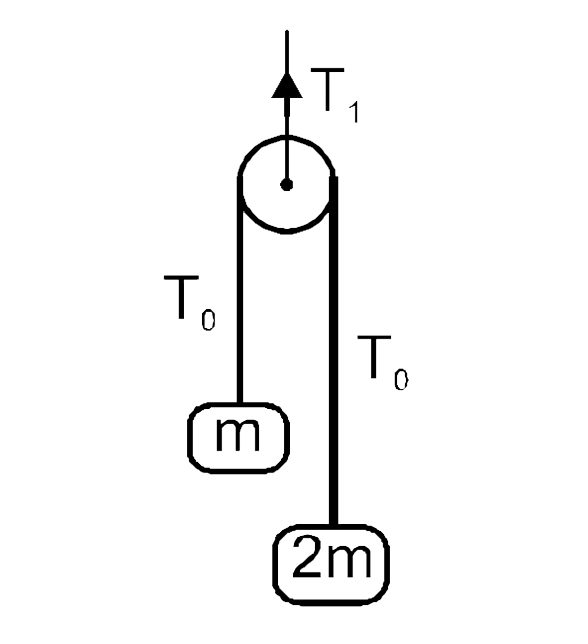
T1=2T0=2[2m(2m)m+2m]g
T1=8m3g=80m3...(i)
In resonance ,
fwire=ftube
(1)V12l1=(1)V24l2
(√T1μ)2(x)=(400)4(x2)
⇒T1=μ(16×104)
From (i), 803m=10−4(16×104)
m=0.6kg.
Topper's Solved these Questions
Similar Questions
A wire of length 2.00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
View SolutionAn air column enclosed in an open pipe is vibrating in its fundamental mode . The fundamental frequency is 30 Hz. If the velocity of sound air is 300ms−1 , find the length of the pipe and frequency of 3rd overtone .
View Solution
Knowledge Check
- Question 1 - Select One
Length of 0.3m wire vibrates in fundamental mode at frequency 480 Hz. The velocity of sound wave in air is
A330 m/sB320 m/sC330 m/sD288 m/s - Question 2 - Select One
Length of 0.3 m wire vibrates in fundamental mode at frequency 480Hz. Then the velocity of sound wave in air is
A330m/sB320m/sC300m/sD288m/s - Question 3 - Select One
Tension applied to a wire of length 1m and its mass 1g, if it is to vibrate with the fundamental frequency of 50 Hz, will be
A100NB10NC50ND2.5N
Consider the situation shown in figure. The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 40ms−1, find the tension in the wire.
 .View Solution
.View SolutionA sonometer wire of length 1 m is stretched by a weight of 10 kg. The fundamental frequency of vibration is 100 Hz. Determine the linear density of material of wire.
View SolutionA sonometer wire of length 0.95 m can bear a maximum stress of 9×108N/m2. Calculate the fundamental frequency produced in the wire if density of wire is 8×103kg/m3.
View SolutionA wire of length 40cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as 340m/s . Find the tension in the wire.
 View Solution
View SolutionA steel piano wire 0.5 m long has a total mass of 0.01 kg and is stretched with a tension of 800 N. The frequency, when it vibrates in its fundamental mode, is
View Solution

