An ideal gas consists of a large number of identical molecules. Absolute temperature of the gas is T(in kelvin). Molecular weight of gas is M and R is gas constant. Mathch the proper entries from column-2 to column-1 using the codes given below the columns. Column−1Column−II(P)Root mean square speed of molecules is greater than(1)√RTM(Q)Most probable speed of molecues is smaller than(2)1.5√RTM(R)Average velocity of a molecule is smaller than(3)2√RTM(S)Speed of a molecule may be greater than(4)2.5√RTM
pqrs2134
pqrs3142
pqrs1324
pqrs4231
Root mean square speed of molecules =√3RTM=1.732√RTM
Most probable speed of molecures =√2RTM=1.44√RTM
Average velocity of a molecule is zero
Speed of any individual molecule may be anything.
Topper's Solved these Questions
Similar Questions
Match the following:
Column-IColumn-II(A) Root mean square velocity(p)√3Pd(B) Average velocity(q)√3RTm(C) Most probable velocity(r)√8Pπd(D) Velocity possessed by maximum fraction of molecules(s)√2RTm
View SolutionFor a monotomic gas at temperature T, match the following columns.
ColumnIColumnII(A)Speed of sound(p)√2RT/M(B)RMS speed of gas molecules(q)√8RT/πM(C)Average speed of gas molecules(r)√3RT/M(D)Most probable speed of gas molecules(s)√5RT/3M
View Solution
Knowledge Check
The root mean square speed of gas molecules
Ais same for all gases at the same temperatureBdepends on the mass of the gas molecule and its temperatureCis independent of the density and pressure of the gasDdepends only on the temperature and volume of the gasThe root mean square speed of the molecules of a gas is
Aindependent of its pressure but directly proportional to its Kelvin temperatureBdirectly proportional to two square root of both its pressure and its Kelvin temperatureCindepdent of its pressure but directly proportional to the square root of its Kelvin temperature.Ddirectly proportional to its pressure and its Kelvin temperature.In column-II, some situations are given, and in column-I, their results are given. Mathc the proper entries from column-2 to column-1 using the codes iven below the columns
 Apqrs3142Bpqrs2134Cpqrs3214Dpqrs2431
Apqrs3142Bpqrs2134Cpqrs3214Dpqrs2431
The absolute temperature of an ideal gas is….. to/than the average kinetic energy of the gas molecules.
View SolutionThe mean square speed of the molecules of a gas at absolute temoerature T is proportional to
View SolutionIn each situation of column-I, some charge distributions are given with all details explained. In column -II The electrostatic potential energy and its nature is given situation in column -II. Match the proper entries from column-2 to column-1 using the codes given below the columns, Column-I
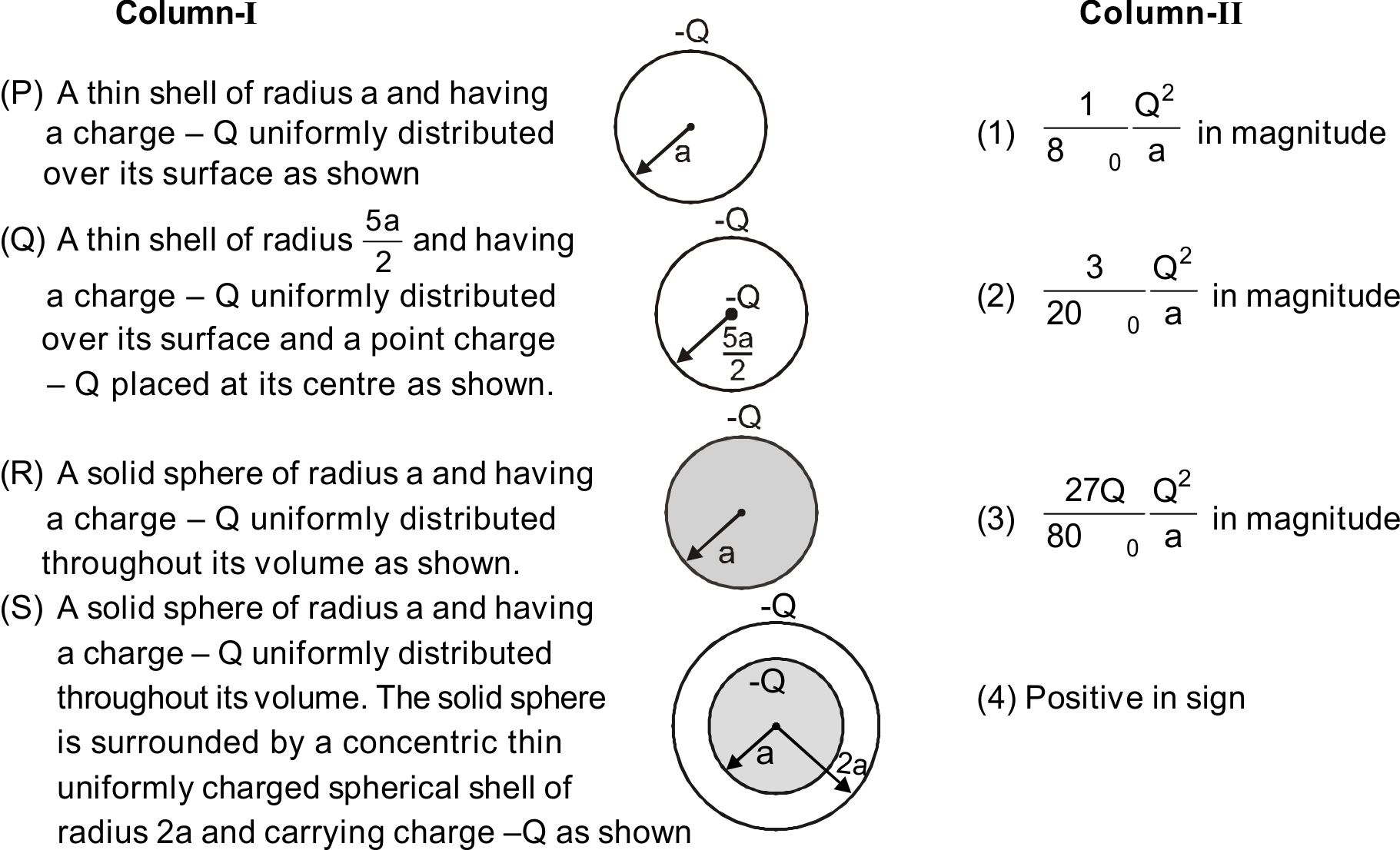
View SolutionThe root mean square velocity of a gas molecule at any temperature T K of a gas molecule of molecular weight M is
View SolutionMatch the following:
Column-IColumn-II(P) R.M.S(1)23NKT(Q) PV(2)KT(R) Average K.E.(3)√3PVM(S) Most probable speed(4)√2RTM
View Solution
