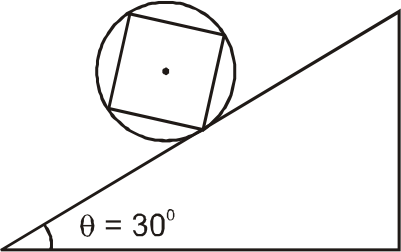
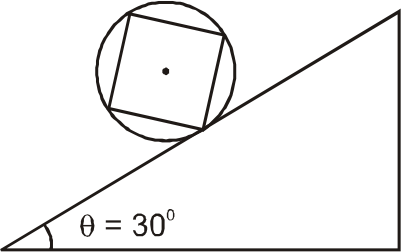
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The acceleration of centre of mass of system is
g2
g4
7g24
g8
I=⎡⎢
⎢
⎢⎣M(R√2)212+M(R√2)2⎤⎥
⎥
⎥⎦×4+mR2
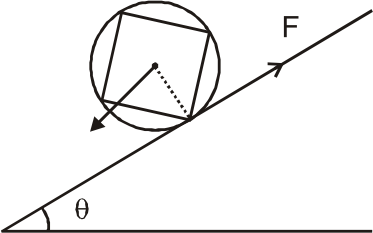
(4M+m)gsinθ−F=(4M+m)a
F.R.=I(aR)
solving a=7g24
F=20a≤μ(4M+m)gcos30
μ≥512√3
∴μmin=512√3
Topper's Solved these Questions
Similar Questions
Find the moment of inertia, about a diameter, of a uniform ring of mass M = 8kg and radius a = 1m?
 View Solution
View SolutionFor identical rods, each of mass m are welded at their ends to form a square, and the corners are then welded to a light metal hoop of radius r. If the rigid assembly of rods and hoop is allowed to roll down the inclined rough surface. If the minimum value of the coefficient of static friction which will prevent slipping is k10 . Find the value of k.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The moment of inertia of system about the axis of ring will be-A20kgm2B40kgm2C10kgm2D60kgm2 - Question 2 - Select One
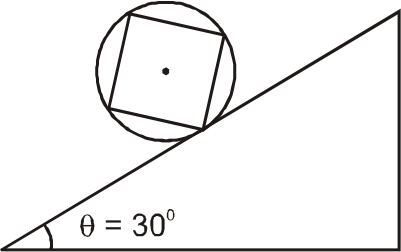
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The minimum value of coefficient of friction to prevent slipping is-A57B512√3C5√37D75√3 - Question 3 - Select One
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR
A rigid body of mass m and radius r starts coming down an inclined plane of inclination θ . Then find out the acceleration of centre of mass if friciton is absent.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
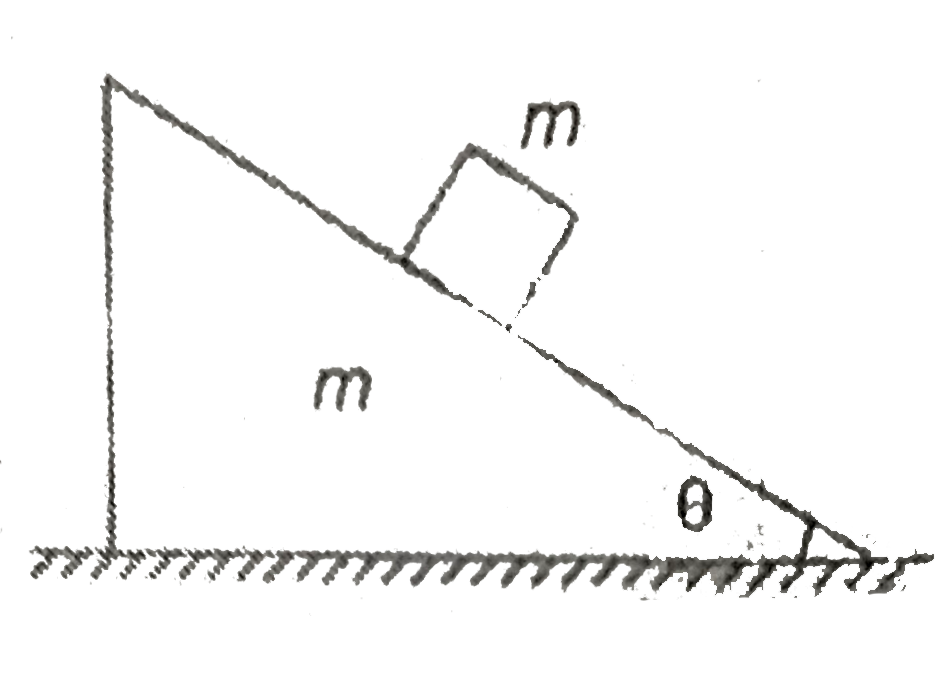 View Solution
View SolutionA ring is allowed to roll down on an incline of 1 in 10 without slipping. The acceleration of its centre of mass is
View Solution

