Let the base of a triangle lie along the line x = a and be of length 2a. The area of this triangles is a2, if the vertex lies on the line
x=−a
x = 0
x=a2
x = 2a
The correct Answer is:B, D
To solve the problem step by step, we need to analyze the given information about the triangle:
1. Understanding the Triangle's Base:
- The base of the triangle lies along the line x=a.
- The length of the base is 2a.
- Since the base is vertical along the line x=a, the endpoints of the base can be represented as (a,y1) and (a,y2) where y1 and y2 are the y-coordinates of the endpoints.
2. Finding the Coordinates of the Base:
- Since the length of the base is 2a, we can set y1=y and y2=y+2a (assuming y1<y2).
- Thus, the coordinates of the base vertices are (a,y) and (a,y+2a).
3. Calculating the Height of the Triangle:
- Let the vertex of the triangle be at point (xv,yv).
- Since the vertex lies on the line x=a, we can set xv=a.
- The height of the triangle will be the vertical distance from the vertex to the base, which can be calculated as h=|yv−y| or h=|yv−(y+2a)|.
4. Using the Area Formula:
- The area A of a triangle is given by the formula:
A=12×base×height
- Here, the base is 2a and the height is h. Therefore, we can write:
A=12×2a×h=a×h
5. Setting Up the Equation:
- We know from the problem that the area of the triangle is a2. Thus, we can set up the equation:
a×h=a2
- Simplifying this gives:
h=a
6. Finding the Vertex's Y-Coordinate:
- Since we have established that the height h is equal to a, we can express this in terms of the y-coordinates:
- If yv is above the base, we have yv−y=a which gives yv=y+a.
- If yv is below the base, we have (y+2a)−yv=a which gives yv=y+2a−a=y+a.
7. Conclusion:
- In both cases, the vertex's y-coordinate is y+a. Thus, the vertex of the triangle can be represented as (a,y+a).
Summary of the Solution:
- The base of the triangle lies along the line x=a with endpoints at (a,y) and (a,y+2a).
- The height of the triangle is a, leading to the vertex being at (a,y+a).
- The base of the triangle lies along the line x=a.
- The length of the base is 2a.
- Since the base is vertical along the line x=a, the endpoints of the base can be represented as (a,y1) and (a,y2) where y1 and y2 are the y-coordinates of the endpoints.
- Since the length of the base is 2a, we can set y1=y and y2=y+2a (assuming y1<y2).
- Thus, the coordinates of the base vertices are (a,y) and (a,y+2a).
- Let the vertex of the triangle be at point (xv,yv).
- Since the vertex lies on the line x=a, we can set xv=a.
- The height of the triangle will be the vertical distance from the vertex to the base, which can be calculated as h=|yv−y| or h=|yv−(y+2a)|.
- The area A of a triangle is given by the formula:
A=12×base×height
- Here, the base is 2a and the height is h. Therefore, we can write:
A=12×2a×h=a×h
- We know from the problem that the area of the triangle is a2. Thus, we can set up the equation:
a×h=a2
- Simplifying this gives:
h=a
- Since we have established that the height h is equal to a, we can express this in terms of the y-coordinates:
- If yv is above the base, we have yv−y=a which gives yv=y+a.
- If yv is below the base, we have (y+2a)−yv=a which gives yv=y+2a−a=y+a.
- In both cases, the vertex's y-coordinate is y+a. Thus, the vertex of the triangle can be represented as (a,y+a).
- The base of the triangle lies along the line x=a with endpoints at (a,y) and (a,y+2a).
- The height of the triangle is a, leading to the vertex being at (a,y+a).
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Passage Based Questions)
6 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Single Integer Answer Type Questions)
5 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Single Option Correct Type Questions)
15 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Knowledge Check
Altitude and base of a right angle triangle are (x+2) and (2x+3) ( in cm ). If the area of the triangle be 60 cm2 , the length of the hypotenuse is :
A21 cmB13 cmC17 cmD15 cmIf the base of a triangle and the ratio of the lengths of the other two unequal sides are given, then the vertex lies on
A. straight lineBcircleCellipseDparabolaThe area of triangle formed by the lines l1andl2 and the x-axis is:
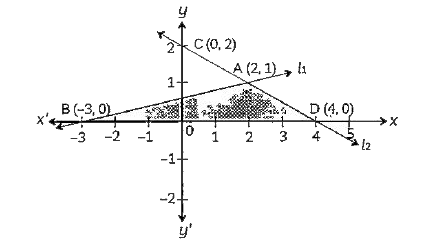 A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. units
A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. units
The base of a triangle lies along x=5 and is of length 1 .The area of triangle is 1. The locus of vertex is
View SolutionThe base of an equilateral triangle is along theline given by 3x+4y=9. If a vertex of the triangle is (1,2), then the length of a side of the triangle is
View SolutionThe vertices of the base of an isosceles triangle lie on a parabola y2=4x and the base is a part of the line y=2x−4. If the third vertex of the triangle lies on the x-axis, its coordinates are
View SolutionLet A(−3,2) and B(−2,1) be the vertices of a triangle ABC. If the centroid of this triangle lies on the line 3x+4y+2=0, then the vertex C lies on the line :
View SolutionAn isosceles triangle is inscribed in the parabolay2=4ax with its base as the line joining the vertex and positive end of the latus rectum of the parabola. If (at2,2at) is the vertex of the triangle then
View Solution