To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
![To evaluate lim(xtoa)[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases. If f(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II.lim(xto1)[](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_AAG_DIF_CAL_C05_SLV_116_Q01.png)
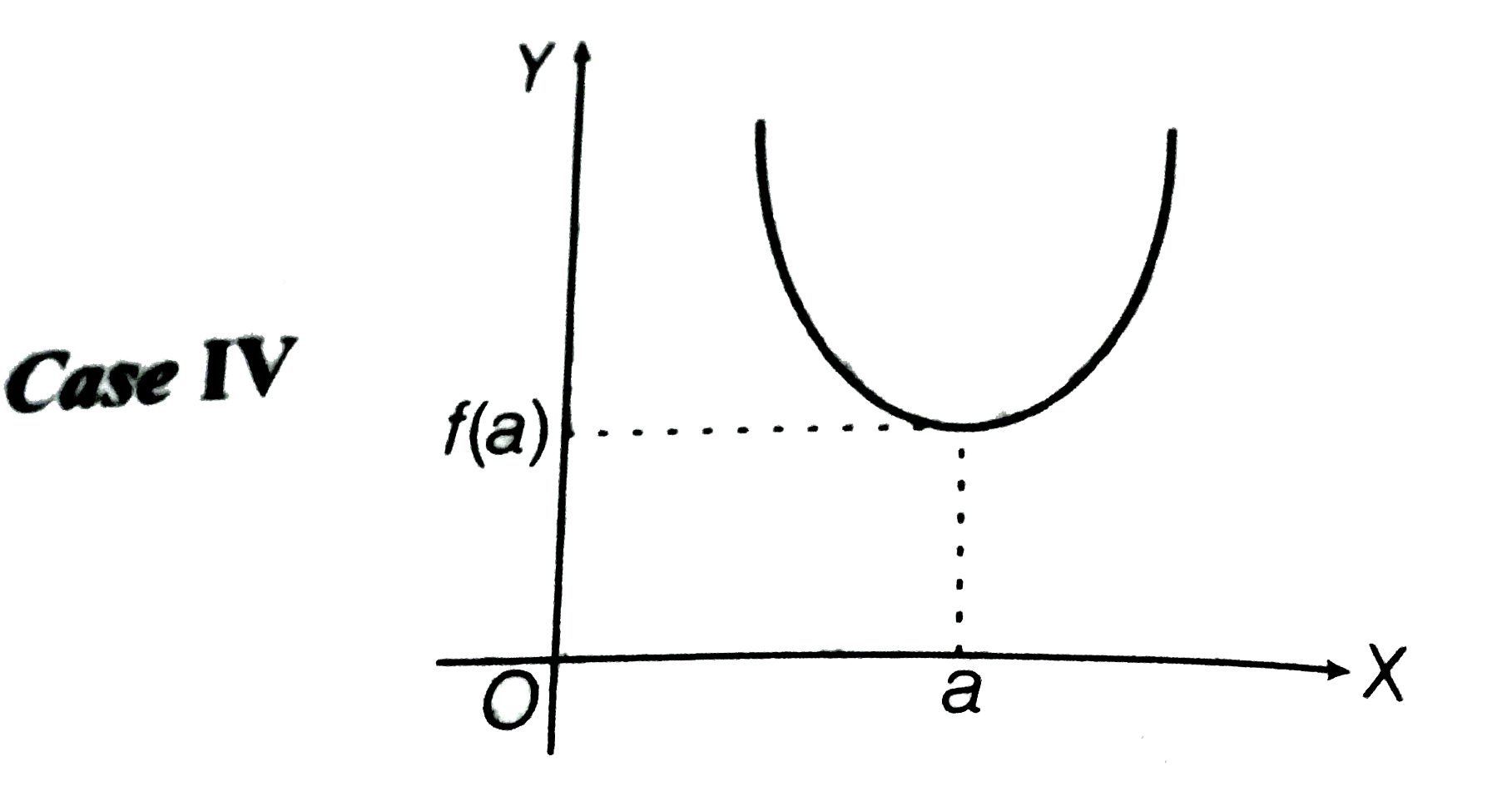
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II.limx→1[cosecπx2]−1/(1−x) is equal to (where [.] denotes the greatest integer function).
0
1
∞
Doesn't exist
The correct Answer is:B
Step by step video & image solution for To evaluate lim_(xtoa)[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases. If f(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II.lim_(xto1)["cosec"(pix)/2]^(-1//(1-x)) is equal to (where [.] denotes the greatest integer function). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Single Option Correct Type Questions)
40 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
Similar Questions
To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
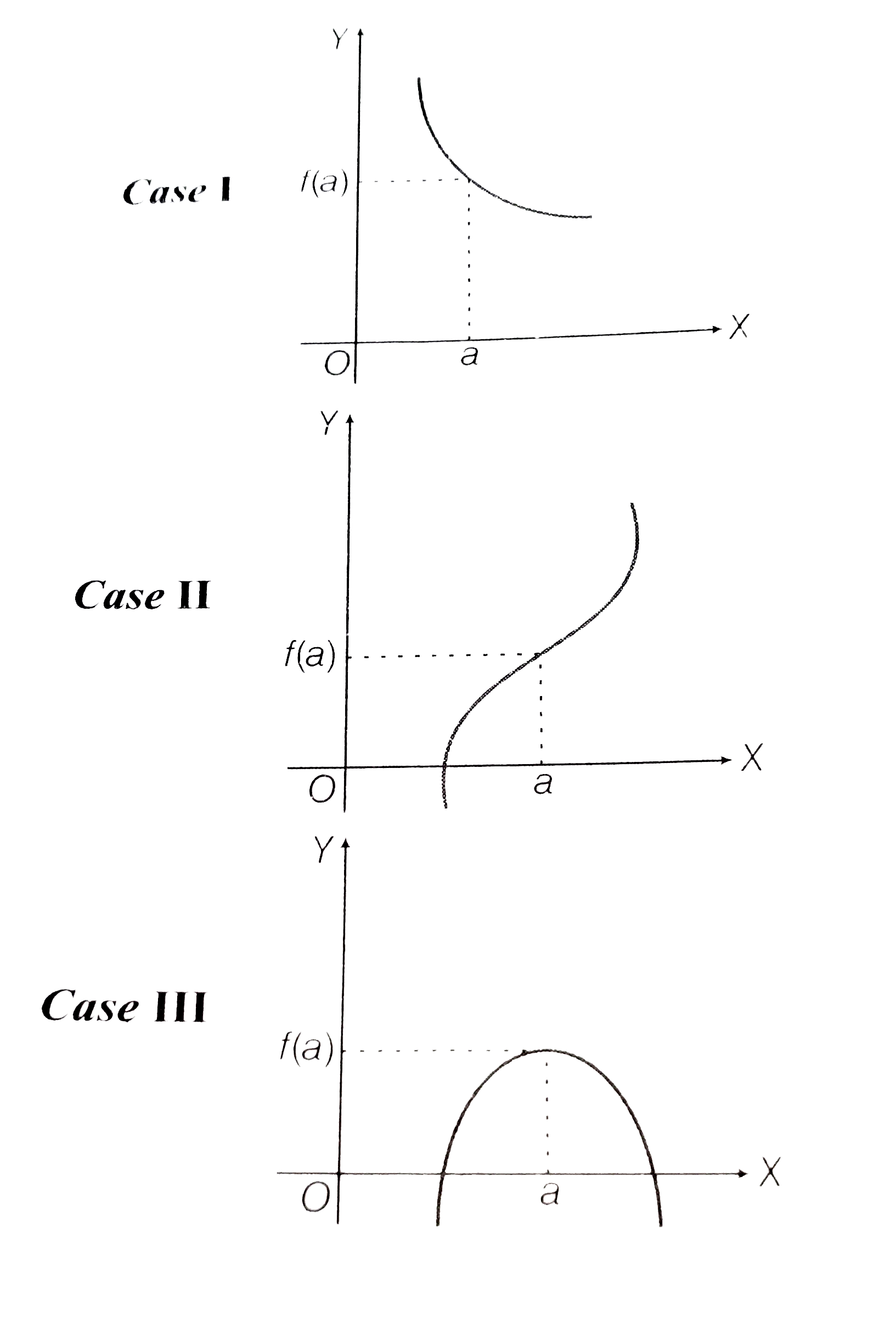
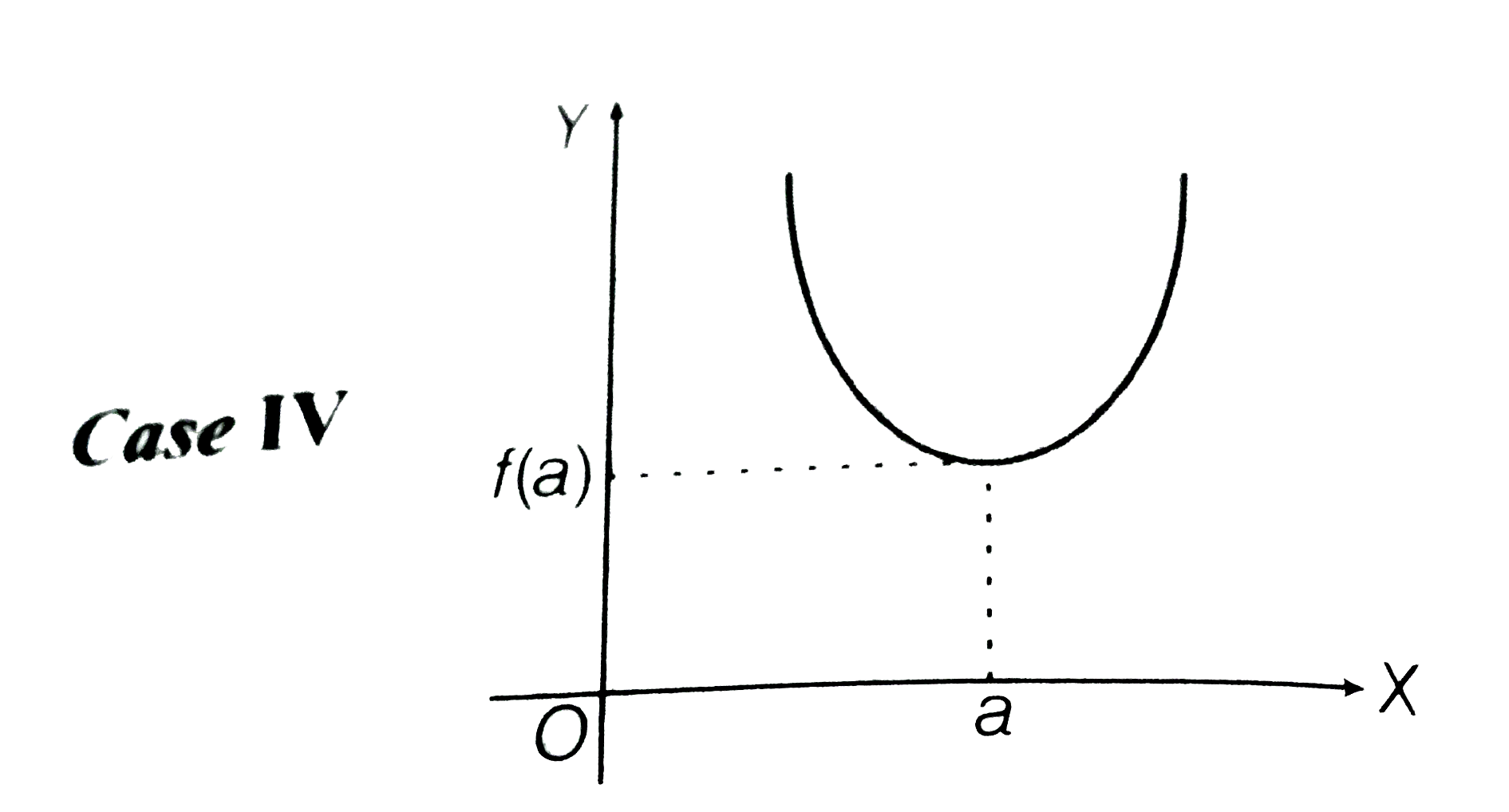
Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II.limx→0[(1−ex).sinx|x|] (where [.] denotes the greatest integer function) equals
View Solutionlimx→1[cosecπx2]1(1−x) (where [.] represents the greatest integer function) is equal to
View Solution
Knowledge Check
limx→1[cosecπx2]1/(1−x) (where [.] represents the greatest integer function) is equal to
A0B1C∞DDoes not existslimx→0[msinxx] is equal to (where mεI and [.] denotes greatest integer function)
Am if m<0Bm−1 if m>0Cm−1, if m<0Dm if m>0limx→0[sin(sgn(x))(sgn(x))], where [.] denotes the greatest integer function, is equal to
A^(2n)pnB^(2n)CnC(2n)!Dnone of these
Let f(x)=(−1)[x] where [.] denotes the greatest integer function), then
View Solutionlimx→1(1−x+[x−1]+[1−x])= where [.] denotes the greatest integer function
View Solutionlimx→1−1([x])1−x where [ .] denotes greatest integer function
View Solutionf(x)=cosec−1[1+sin2x], where [⋅] denotes the greatest integer function.
View Solutionlimx→1(1+x+[x−1]+[1−x]) is equal to (where [ ] denotes greatest integer function)
View Solution
