A circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of ΔABC and S(x) be the area of shaded region.
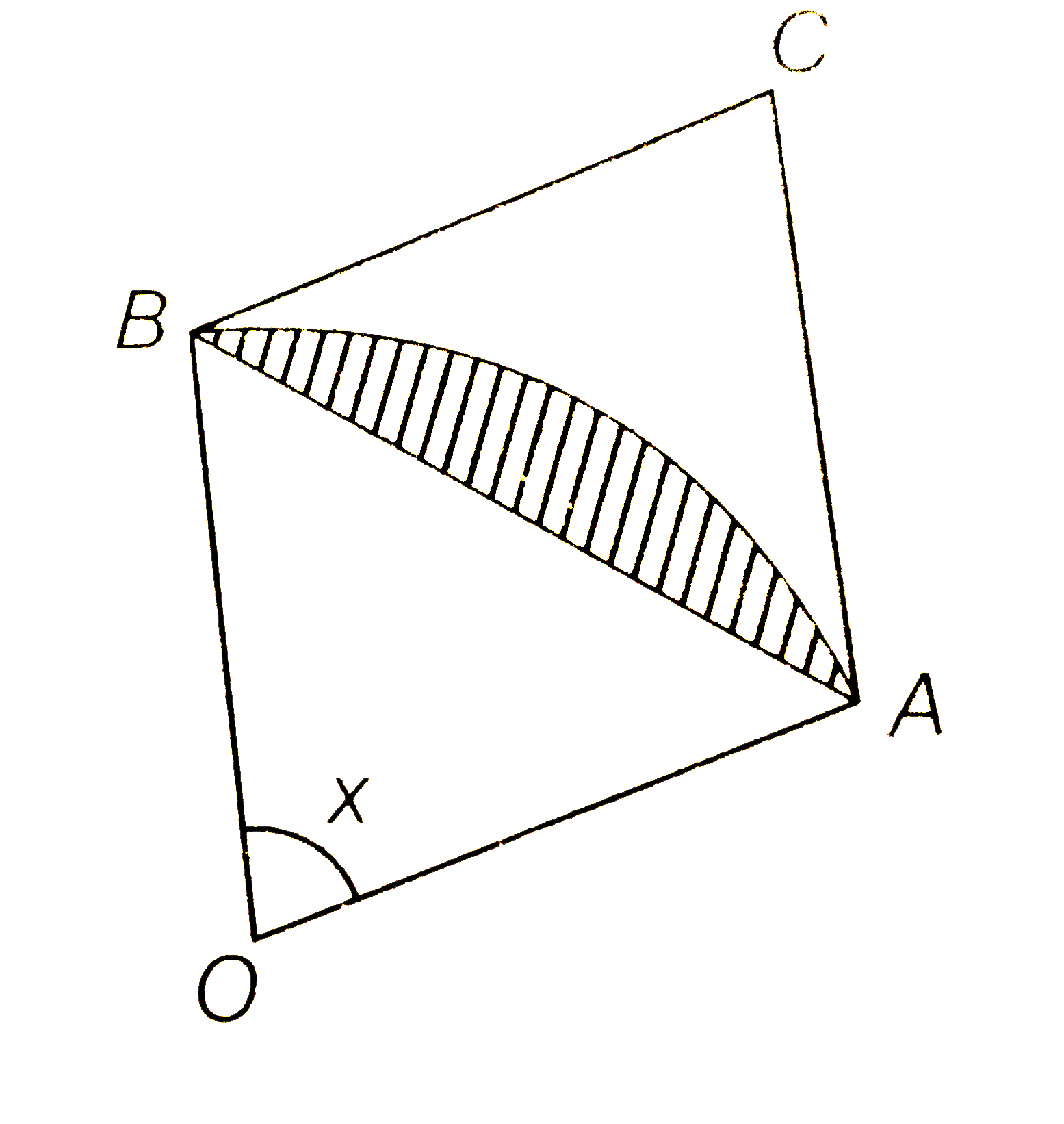
limx→0T(x)x3 is
12
13
14
18
The correct Answer is:D
Step by step video & image solution for A circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of DeltaABC and S(x) be the area of shaded region. lim_(xto0)(T(x))/(x^(3)) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Matching Type Questions)
3 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Single Integer Answer Type Questions)
27 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
Similar Questions
A circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of ΔABC and S(x) be the area of shaded region.
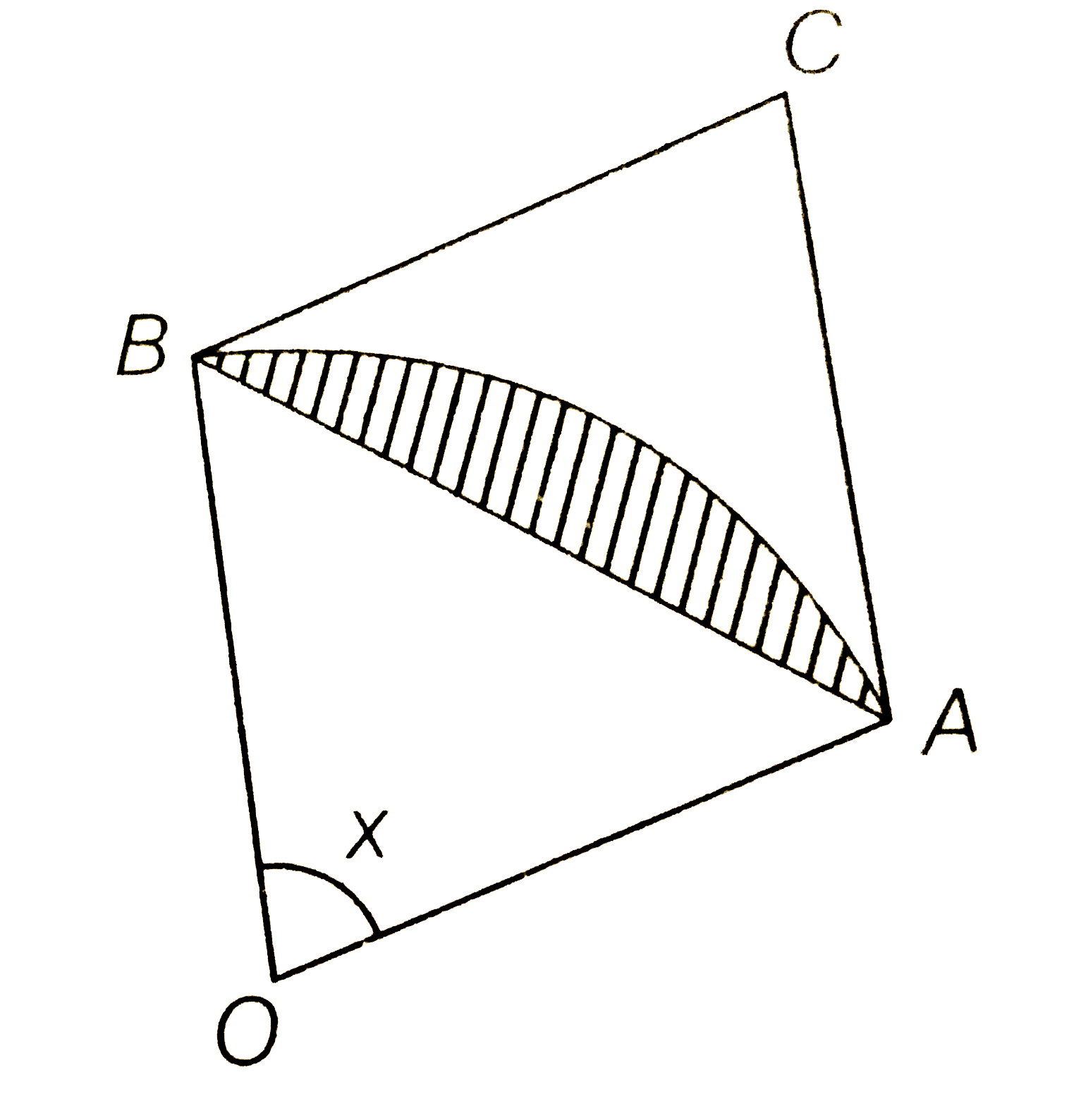
limx→0S(x)x is
View SolutionA circular are of radius 1 subtends an angle of x radians 0<x<π2 as shown in the figure . the point r is the intersection of the two tangent line at P and Q. let T(x) be the area of triangle PQR and S(x) be the area of the shaded region then find T(x)&S(x)&limx→0T(x)S(x)
View Solution
Knowledge Check
In a circle of radius 14 cm, an arc subtends an angle of 120∘ at the centre. If √3=1.73 then the area of the segment of the circle is
A120.56cm2B124.63cm2C118.24cm2D130.57cm2Equation of the tangent to the circle at the point (1, -1) whose centre is the point of intersection of the straight lines x-y=1 and 2x+y-3=0, is
A3x-y-4=0Bx+4y+3=0Cx-3y-4=0D4x+y-3=0In the adjoining figure O is the centre of the circle with radius r’ AB, CD and EF are the diameters of the circle. angleOAF = angleOCB = 60^(@) . What is the area of the shaded region?
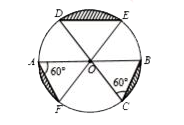 Ar22(π−3√32)Br22(π−3√34)Cr23(π−2√33)DData insuffincient
Ar22(π−3√32)Br22(π−3√34)Cr23(π−2√33)DData insuffincient
A circular are of radius 1 subtends an angle of x radians 0<x<π2 as shown in the figure . the point r is the intersection of the two tangent line at P and Q. let T(x) be the area of triangle PQR and S(x) be the area of the shaded region then find T(x)&S(x)&limx→0T(x)S(x)
View SolutionA circle are PQ of radius an angle s radius 0<x<π2 point R is the point of intersection of tangents at PandQ on the are Let T(x) be the area of ΔPQR,S(x) be the area of setor OPQ and T(x) be area of ΔOPQ
View SolutionThe equation of the circle with radius 3 and centre as the point of intersection of the lines 2x+3y=5,2x−y=1 is
View SolutionAn arc AB of a cricle subtends an angle x radians at the centre O of the circle, Given that the area of the sector AOB is equal to the square of the length of the arc AB, find the volume of x.
View SolutionA straight line is drawn through the centre of the circle x2+y2−1ax=0 parallel to the straight line x+2y=0 and intersection the circle at AandB. Then the area of AOB is
View Solution
