The figure shows a right triangle with its hypotenuse OB along the Y-axis and its vertex A on the parabola y=x2.
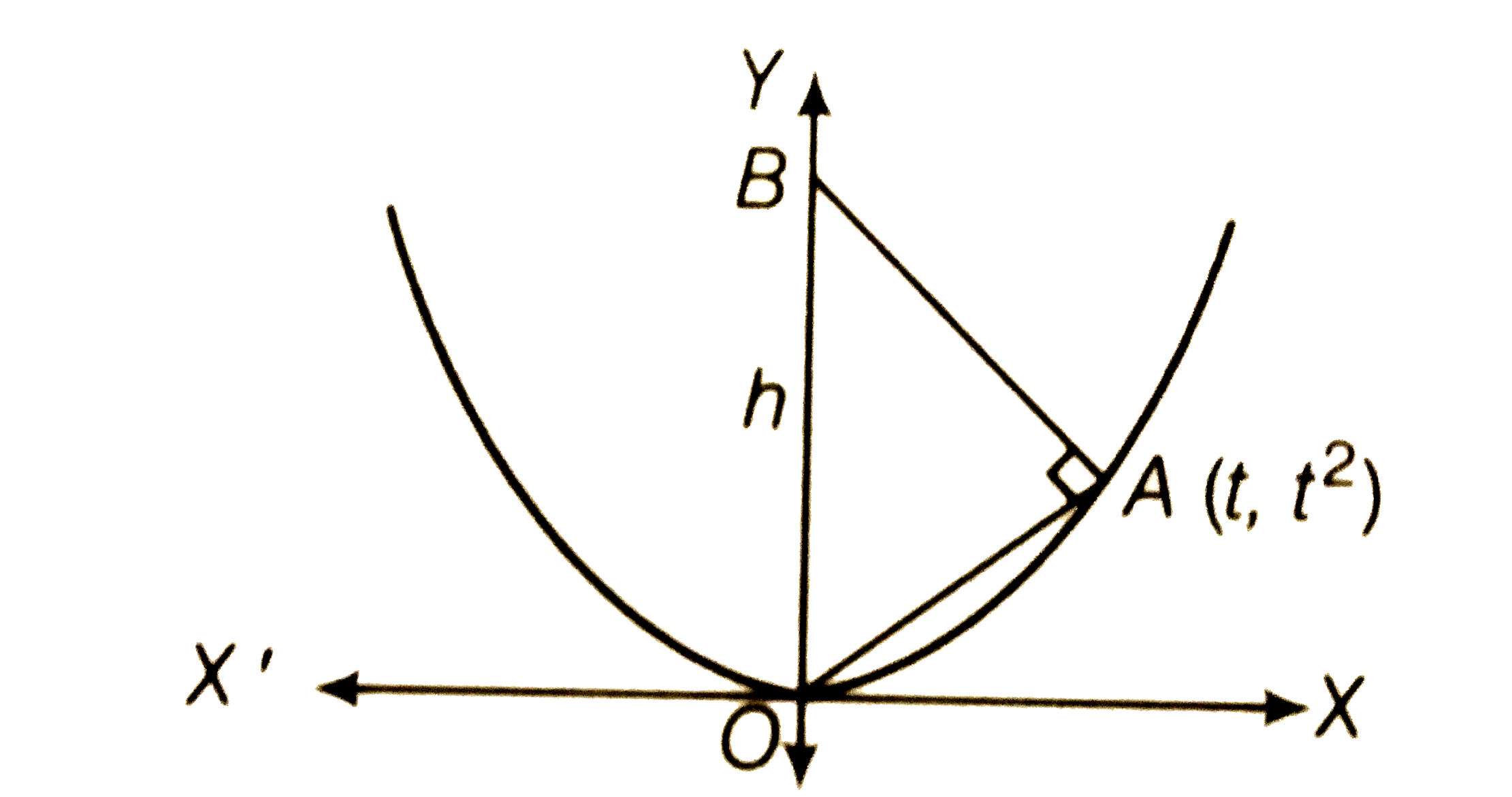
The figure shows a right triangle with its hypotenuse OB along the Y-axis and its vertex A on the parabola y=x^(2). Let h represents the length of the hypotenuse which depends on the x-coordinate of the point A. The value of lim(t to 00)(h) is equal to
Let h represents the length of the hypotenuse which depends on the x-coordinate of the point A. The value of limt→00(h) is equal to

A

0

B

1/2

C

1

D

2

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Updated on:21/07/2023
|
Answer

Step by step video & image solution for The figure shows a right triangle with its hypotenuse OB along the Y-axis and its vertex A on the parabola y=x^(2). Let h represents the length of the hypotenuse which depends on the x-coordinate of the point A. The value of lim_(t to 00)(h) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSAPPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The figure shows a right triangle with its hypotenuse OB along the y-axis and its vertex A on the parabola y=x2. Let h represents the length of the hypotenuse which depends on the x- coordinate of the point A. The values of Limx→0(h) equals
    ocr_image

    A0
    B1/2
    C1
    D2

  • The parabola having its focus at (3, 2) and directrix along the y-axis has its vertex at

    A(2,2)
    B(32,2)
    C(12,2)
    D(23,2)

  • An isosceles right angled triange is in scribed in the circle x2+y2=r2. If the coordinates of an end of the hypotenuse are (a,b) the coordinates of the vertex are

    A(−a,−b)
    B(b,−a)
    C(b,a)
    D(−b,−a)