f(x)={x−[x],if[x]is odd1+[x]−x,if[x] is even
Then, the value of π210∫10−10f(x)cosπ×dx is
The correct Answer is:4
Topper's Solved these Questions
- DEFINITE INTEGRALBOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 1
15 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise For Session 2
14 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
- DETERMINANTS BOOK - ARIHANT MATHSCHAPTER - DETERMINANTS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
Similar Questions
For any real number x, let [x] denote the largest integer less than or equal to x, Let f be a real-valued function defined on the interval [−10,10] be f(x)={x−[x],if[x] is odd, 1+[x]−x,if[x] is even Then the value of π210∫10−10f(x)cosπxdx is____
View Solutionf(x)={e−ex−[x]if[x]isoddex−[x]if[x]iseven ,then find the value of 2e∫3−3f(x)dx
View Solution
Knowledge Check
For any real number x, let [x] denotes the largest integer less than or equal to x.Let f be a real valued function defined on the interval[-10,10] by
f(x)={(x−[x])<br>(1+[x]−x)}
Then, the value of π210∫10−10 f(x) cos π x dx isA2B4C0DNone of theseLet f be an odd function then ∫1−1(|x|+f(x)cosx)dx is equal to
A0B1C2Dnone of theseThe value of the integral ∫π/20f(x)f(x)+f(π2−x)dx is
Aπ/4Bπ/2CπD0
If f(x)=x+sinx, then find the value of ∫2ππf−1(x)dx.
View SolutionIf f(x)=x+sinx, then find the value of ∫2ππf−1(x)dx.
View SolutionFor any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
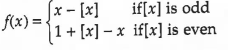 Then, the value of (π10)2(∫10−10f(x)cosπxdx is
Then, the value of (π10)2(∫10−10f(x)cosπxdx is
View SolutionIf f(x) is an odd function, then the value of ∫a−a(f(sinx)f(cosx)+f(sin2x))dx is equal to
View SolutionThe value of the integral ∫π/20f(x)f(x)+f(π2−x)dx is
View Solution
