The side of a triangle are 22 cm, 28 cm, and 36 cm So, find the area of a the circumscribed circle.
To find the area of the circumscribed circle of a triangle with sides 22 cm, 28 cm, and 36 cm, we will follow these steps:
Step 1: Calculate the semi-perimeter (s) of the triangle
The semi-perimeter s is calculated using the formula:
s=a+b+c2
where a=22cm, b=28cm, and c=36cm.
Substituting the values:
s=22+28+362=862=43cm
Step 2: Calculate the area (Δ) of the triangle using Heron's formula
Heron's formula for the area of a triangle is:
Δ=√s(s−a)(s−b)(s−c)
Substituting the values:
Δ=√43(43−22)(43−28)(43−36)
Calculating each term:
s−a=43−22=21s−b=43−28=15s−c=43−36=7
Now substituting these back into the formula:
Δ=√43×21×15×7
Step 3: Calculate the circumradius (R)
The circumradius R of a triangle can be calculated using the formula:
R=abc4Δ
Substituting the values:
R=22×28×364Δ
Step 4: Calculate the area of the circumscribed circle
The area A of the circumscribed circle is given by:
A=πR2
Substituting the value of R:
A=π(abc4Δ)2
Step 5: Substitute values and simplify
Substituting a=22, b=28, c=36, and Δ calculated from Step 2:
A=π(22×28×364Δ)2
Step 6: Calculate the numerical value
Now, we can calculate the numerical value of A using Δ calculated from Step 2.
Final Calculation
After performing the calculations, we find:
A≈1018.82cm2
The semi-perimeter s is calculated using the formula:
s=a+b+c2
where a=22cm, b=28cm, and c=36cm.
s=22+28+362=862=43cm
Heron's formula for the area of a triangle is:
Δ=√s(s−a)(s−b)(s−c)
Substituting the values:
Δ=√43(43−22)(43−28)(43−36)
Calculating each term:
s−a=43−22=21s−b=43−28=15s−c=43−36=7
Now substituting these back into the formula:
Δ=√43×21×15×7
The circumradius R of a triangle can be calculated using the formula:
R=abc4Δ
Substituting the values:
R=22×28×364Δ
The area A of the circumscribed circle is given by:
A=πR2
Substituting the value of R:
A=π(abc4Δ)2
Substituting a=22, b=28, c=36, and Δ calculated from Step 2:
A=π(22×28×364Δ)2
Now, we can calculate the numerical value of A using Δ calculated from Step 2.
After performing the calculations, we find:
A≈1018.82cm2
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 4
8 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 5
7 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 2
19 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Knowledge Check
The sides of a triangle are 11 cm, 60 cm and 61 cm. What is the radius of the circile circumscribing the triangle ?
A31 cmB30 cmC30.5 cmD31.5 cmThe sides of triangle are 13 cm, 14 cm and 15 cm. The area of the triangle is
A84cm2B91cm2C105cm2D97.5cm2The angles of a triangle are in the ratio 2:3:7 and the radius of the circumscribed circle is 10 cm . The length of the smallest side is
A2 mB5 cmC7 cmD10 cm
The sides of a triangle are 5 cm, 12 cm and 13 cm. Then its area is :
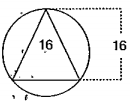
View SolutionIn the following diagram, the height and base of an isosceles triangle are 16 cm each. Find the area of the circumscribing circle.
View SolutionA triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26cm,28cm and 30cm, and the parallelogram stands on the base 28cm, find the height of the parallelogram.
View SolutionThe area of a triangle whose sides are 9 cm , 12 cm and 15 cm is
View SolutionThe area of a triangle whose sides are 9 cm , 12 cm and 15 cm is
View Solution
