I(n) is the area of n sided refular polygon inscribed in a circle unit

If r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
A $\frac{a}{2} cot (\frac{π}{2 n})$
B $\frac{a}{2} cot (\frac{π}{n})$
C $\frac{a}{2} tan (\frac{π}{n})$
D $\frac{a}{2} cos (\frac{π}{n})$
The area of the circle and the area of a regular polygon of n sides and the perimeter equal to the circle are in the ratio of
A $tan (\frac{π}{n}) : \frac{π}{n}$
B $cos (\frac{π}{n}) : \frac{π}{n}$
C $sin (\frac{π}{n}) : \frac{π}{n}$
D $cot (\frac{π}{n}) : \frac{π}{n}$
In the following figure a wire bent in the form of a regular polygon of $n$ sides is inscribed in a circle of radius $a$ . Net magnetic field at centre will be

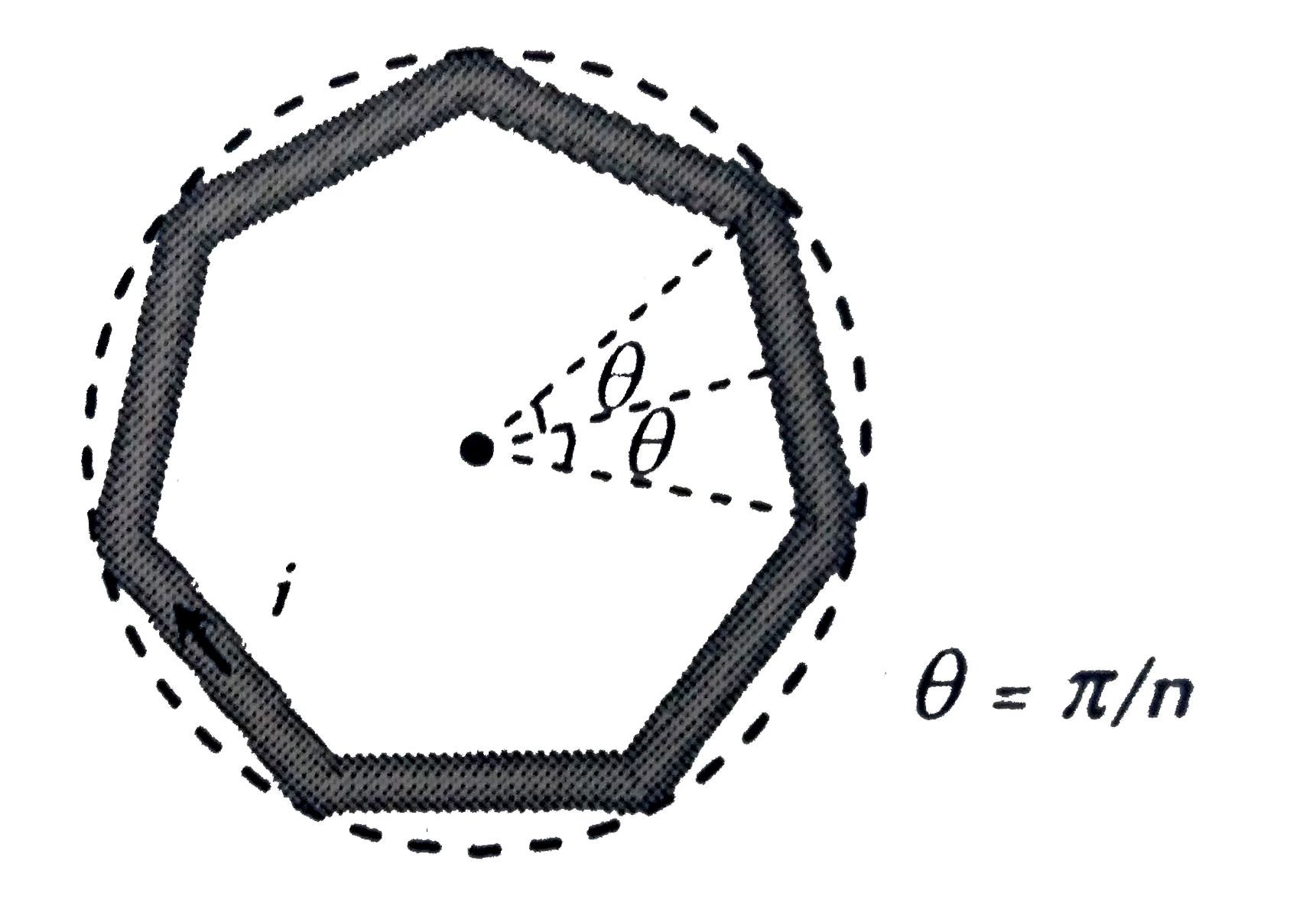A $\frac{μ_{0} i}{2 π a} tan \frac{π}{n}$
B $\frac{μ_{0} n i}{2 π a} tan \frac{π}{n}$
C $\frac{2}{π} \frac{n i}{a} μ_{0} tan \frac{π}{n}$
D $\frac{n i}{2 a} μ_{0} tan \frac{π}{n}$

$I_{n}$ is the area of n sided refular polygon inscribed in a circle unit radius and $O_{n}$ be the area of the polygon circumscribing the given circle, prove that $I_{n} = \frac{O_{n}}{2} ⎛ ⎝ 1 + \sqrt{1 - {(\frac{2 I_{n}}{n})}^{2}} ⎞ ⎠$