In a right angled triangle ABC, the bisector of the right angle C divides AB into segment x and y and tan(A−B2)=t, then x:y is equal to
A
(1+t)=(1−t)
B
(1−t):(t+1)
C
1:(1+t)
D
(1−t):1
Text Solution
The correct Answer is:B
|
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (More Than One Correct Option Type Questions)
24 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Statement I And Ii Type Questions)
15 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 8
5 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Knowledge Check
In a triangle ABC, right angled at C, find the value of tan A + tan B in terms of the sides a,b,c.
Aa2bcBa+bCb2acDc2abABC is right angled triangle, right angled at C . D is the midpoint of BC. Then , tanθtanϕ =
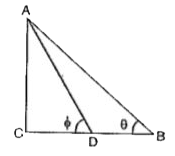 A1B1√2C12D2
A1B1√2C12D2
In right angled triangle ABC, right angled at C, show that tanA+tanB=c2ab.
View SolutionIn a right -angled triangle ABC, right-angled at B, if AB=2√6andAC−BC=2, then find secA+tanA.
View SolutionIn a right angle triangle ABC, αandβ are the two angles other than right angle, if β=30∘, then what is tanα equal to?
View SolutionIn a right angle triangle ABC, αandβ are the two angles other than right angle, if α=60∘, then what is tanβ equal to?
View SolutionIn a right-angled triangle ABC, right angled at B, AB = x2, BC = x+2 and AC = x+3. Find value of x.
View Solutionif in triangle ABC right angled at C then tanA+tanB
View Solution
