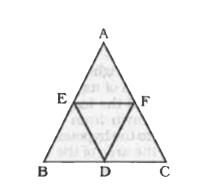
D,E and F are the middle points of the sides of the triangle ABC, then
centroid of the triangle DEF is the same as that of ABC
orthocentre of the traiangl DRF is the circumcentre of ABC
orthocentre of the triangle DEF is the incentre of ABC
centroid of the triangle DEF is not the same as that of ABC
The correct Answer is:A, B
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Statement I And Ii Type Questions)
15 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Passage Based Questions)
25 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Single Option Correct Type Questions)
65 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
D,E,andF are the middle points of the sides of the triangle ABC , then (a) centroid of the triangle DEF is the same as that of ABC (b) orthocenter of the tirangleDEF is the circumcentre of ABC
View SolutionIf D, E and F are the mid-points of the sides of an equilateral triangle ABC, then the ratio of the area of triangle DEF and DCF is :
View Solution
Knowledge Check
Let D be the middle point of the side BC of a triangle ABC. If the triangle ADC is equilateral, then a2:b2:c2 is equal to
A1:4:3B4:1:3C4:3:1D3:4:1Let D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0B0C2DNone of these
If D, E and F are the mid-points of the sides of a △ABC , the ratio of the areas of the triangles DEF and ABC is .......
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View SolutionFind the area of a triangle ABC if the coordinates of the middle points of the sides of the triangle are (−1,−2),(6,1)and(3,5)
View SolutionFind the area of a triangle ABC if the coordinates of the middle points of the sides of the triangle are (−1,−2),(6,1)and(3,5)
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View Solution
