A block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
mg
mg sin θ
μmgcosθ
μmgsinθ
The correct Answer is:A
To solve the problem of finding the net force exerted by the surface on a block of mass m resting on a rough inclined plane with a friction coefficient μ, we can follow these steps:
Step 1: Identify Forces Acting on the Block
The forces acting on the block are:
1. The gravitational force (→W) acting downward, which can be expressed as W=mg, where g is the acceleration due to gravity.
2. The normal force (→N) exerted by the inclined plane on the block, acting perpendicular to the surface.
3. The frictional force (→Ffriction) acting parallel to the surface, opposing the motion.
Step 2: Resolve the Weight into Components
The weight of the block can be resolved into two components:
- A component parallel to the incline: W∥=mgsinθ
- A component perpendicular to the incline: W_{\perpendicular} = mg \cos \theta
Step 3: Apply Equilibrium Conditions
Since the block is at rest, the net force acting on it must be zero. Therefore, we can set up the following equilibrium conditions:
1. In the direction perpendicular to the incline:
N=mgcosθ
(The normal force balances the perpendicular component of the weight.)
2. In the direction parallel to the incline:
Ffriction=mgsinθ
(The frictional force balances the parallel component of the weight.)
Step 4: Calculate the Net Force Exerted by the Surface
The net force exerted by the surface on the block is the vector sum of the normal force and the frictional force. Since these two forces are perpendicular to each other, we can use the Pythagorean theorem to find the resultant force:
Fnet=√N2+F2friction
Substituting the expressions we found:
Fnet=√(mgcosθ)2+(mgsinθ)2
Step 5: Simplify the Expression
Using the identity cos2θ+sin2θ=1:
Fnet=√m2g2(cos2θ+sin2θ)=√m2g2=mg
Conclusion
The net force exerted by the surface on the block is:
Fnet=mg
Final Answer
The net force exerted by the surface on the block is mg.
---
The forces acting on the block are:
1. The gravitational force (→W) acting downward, which can be expressed as W=mg, where g is the acceleration due to gravity.
2. The normal force (→N) exerted by the inclined plane on the block, acting perpendicular to the surface.
3. The frictional force (→Ffriction) acting parallel to the surface, opposing the motion.
The weight of the block can be resolved into two components:
- A component parallel to the incline: W∥=mgsinθ
- A component perpendicular to the incline: W_{\perpendicular} = mg \cos \theta
Since the block is at rest, the net force acting on it must be zero. Therefore, we can set up the following equilibrium conditions:
N=mgcosθ
(The normal force balances the perpendicular component of the weight.)
Ffriction=mgsinθ
(The frictional force balances the parallel component of the weight.)
The net force exerted by the surface on the block is the vector sum of the normal force and the frictional force. Since these two forces are perpendicular to each other, we can use the Pythagorean theorem to find the resultant force:
Fnet=√(mgcosθ)2+(mgsinθ)2
Using the identity cos2θ+sin2θ=1:
Fnet=√m2g2(cos2θ+sin2θ)=√m2g2=mg
The net force exerted by the surface on the block is:
Fnet=mg
The net force exerted by the surface on the block is mg.
Topper's Solved these Questions
Similar Questions
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass 5 kg is at rest on a rough inclined surface. If angle of inclination of plane is 60∘, then force applied by it on block is
View Solution
Knowledge Check
A block of mass 3kg is at rest on a rough inclined plane as shown in the figure. The magnitude of net force exerted by the surface on the block will be
 A26NB19.5NC10ND30N
A26NB19.5NC10ND30NA block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
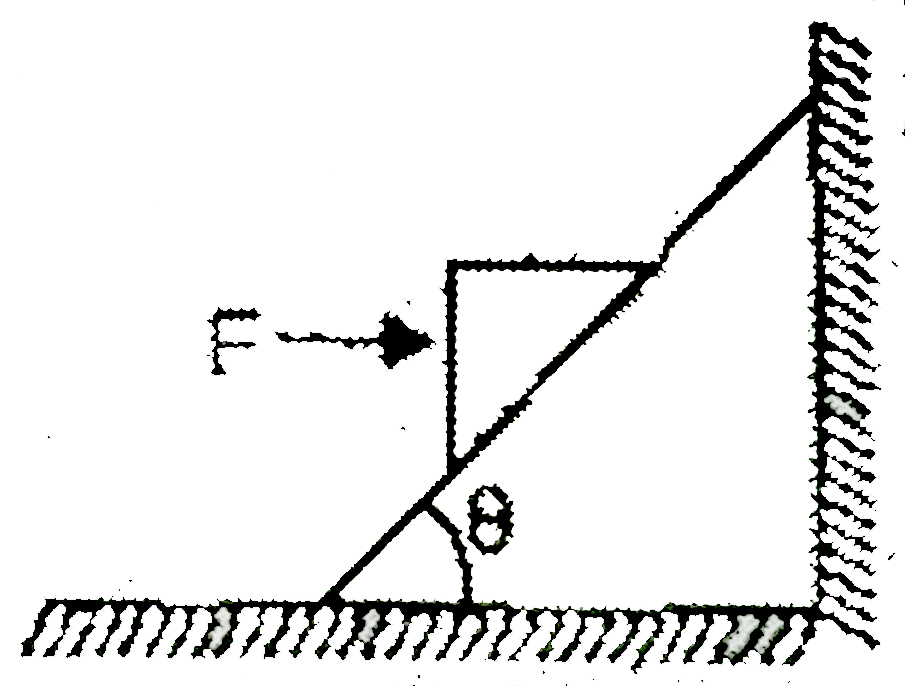
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μA triangular block of mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal forces F is applied to it as shown in figure below, then the correct statements is:
 AFriction force is zero when Fcosθ=mgsinθBThe value of limiting friction is μ(mgsinθ+Fcosθ)CNormal reaction on the block is Fsinθ+mgcosθDThe value of limiting friction is μ(mgsinθ−Fcosθ)
AFriction force is zero when Fcosθ=mgsinθBThe value of limiting friction is μ(mgsinθ+Fcosθ)CNormal reaction on the block is Fsinθ+mgcosθDThe value of limiting friction is μ(mgsinθ−Fcosθ)
A block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block

View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View SolutionA triangular block mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal force F is applied to it as shown in figure below, then the correct statement is :
View SolutionA block of mass m=1/3 kg is kept on a rough horizontal plane. Friction coefficient is μ=0.75. The work done by minimum force required to drag to the block along the plane by a distance 5m is :-
View Solution