Question

स्थिर विद्युत् के अन्तर्गत गॉस का प्रमेय लिखिए एवं सिद्ध कीजिए | आवेश के अनन्त समतल चादर के समीप विद्युत् क्षेत्र की तीव्रता के लिए व्यंजक ज्ञात कीजिए |

Explanation

गॉस का प्रमेय - लघु उत्तरीय प्रश्न क्रमांक 22 देखिए |
आवेश के अनन्त समतल चादर के कारण विधुत क्षेत्र की तीव्रता-आवेश के एक अनन्त समतल चादर की कल्पना करो जिसके दोनों पृष्ठों के प्रति एकांक क्षेत्रफल पर धन आवेश की मात्रा (पृष्ठ घनत्व) `sigma` है | सममिति से स्पष्ट है कि आवेशित चादर के कारण विधुत क्षेत्र चादर के दोनों ओर उसके लम्बवत बाहर की ओर होगा |
मानलो चादर से r दूरी पर एक बिन्दु P है जिस पर विधुत क्षेत्र की तीव्रता ज्ञात करनी है | चादर के दूसरी ओर r दूरी पर दूसरी बिन्दु P' इस प्रकार लो कि PP' चादर के लम्बवत हो |
अब चादर के आर - पार PP' अक्ष वाले एक बेलन की रचना करते हैं | मानलो इस बेलन के वृत्तीय सिरों का क्षेत्रफल A है | तब बेलन का बन्द पृष्ठ गॉसीय पृष्ठ की तरह व्यवहार करेगा |

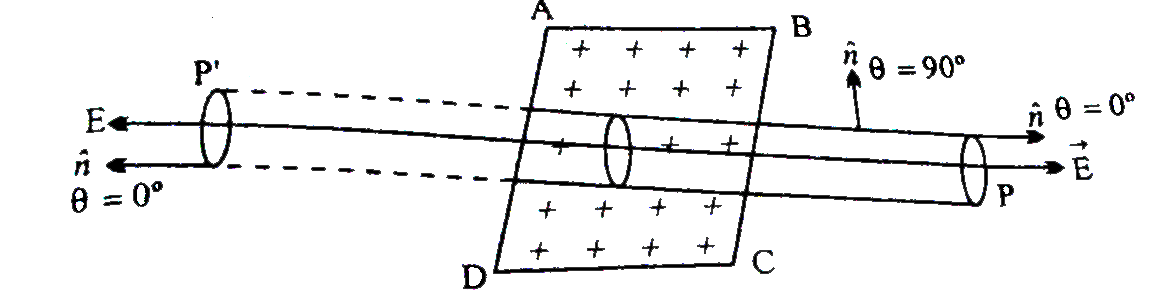
`:." गॉस पृष्ठ के अन्दर कुल आवेश "q=sigmaA" "...(1)`
बेलन का वक्र पृष्ठ विधुत क्षेत्र के समान्तर है अत: वक्र पृष्ठ से गुजरने वाला विधुत फ्लक्स शून्य होगा `(theta=90^(@))` |
अत: बेलन के वृत्तीय सिरों से गुजरने वाला सम्पूर्ण विधुत फ्लक्स `phi_(E)=E.A.+E.A" "(because" दोनों वृत्तीय पृष्ठों में विधुत क्षेत्र बाहर की ओर है")`
या `" "phi_(E)=2EA" "...(2)`
परन्तु गॉस के प्रमेय से,
`phi_(E)=(q)/(epsilon_(0))" "...(3)`
समीकरण (2) और (3) से,
`2EA=(q)/(epsilon_(0))" या "E=(q)/(2epsilon_(0)A)`
समीकरण (1) से मान रखने पर,
`E=(sigmaA)/(2epsilon_(0)A)" या "E=(sigma)/(2epsilon_(0))`
स्पष्ट है कि विधुत क्षेत्र की तीव्रता r पर निर्भर नहीं करती | अत: आवेशित चादर के समीप विधुत क्षेत्र की तीव्रता एकसमान होती है |