दो आवेशित चालकों की धारिताए क्रमश : C1 और C2 है | उन्हें Q1 और Q2 आवेश देने पर उनके विभव क्रमश : V1 और V2 हो जाते है | यदि उन्हें तार से जोड़े दिया , तो निम्नलिखित की गणन कीजिए - (i) उभयनिष्ठ विभव (ii) सयोजन में ऊर्जा हास |
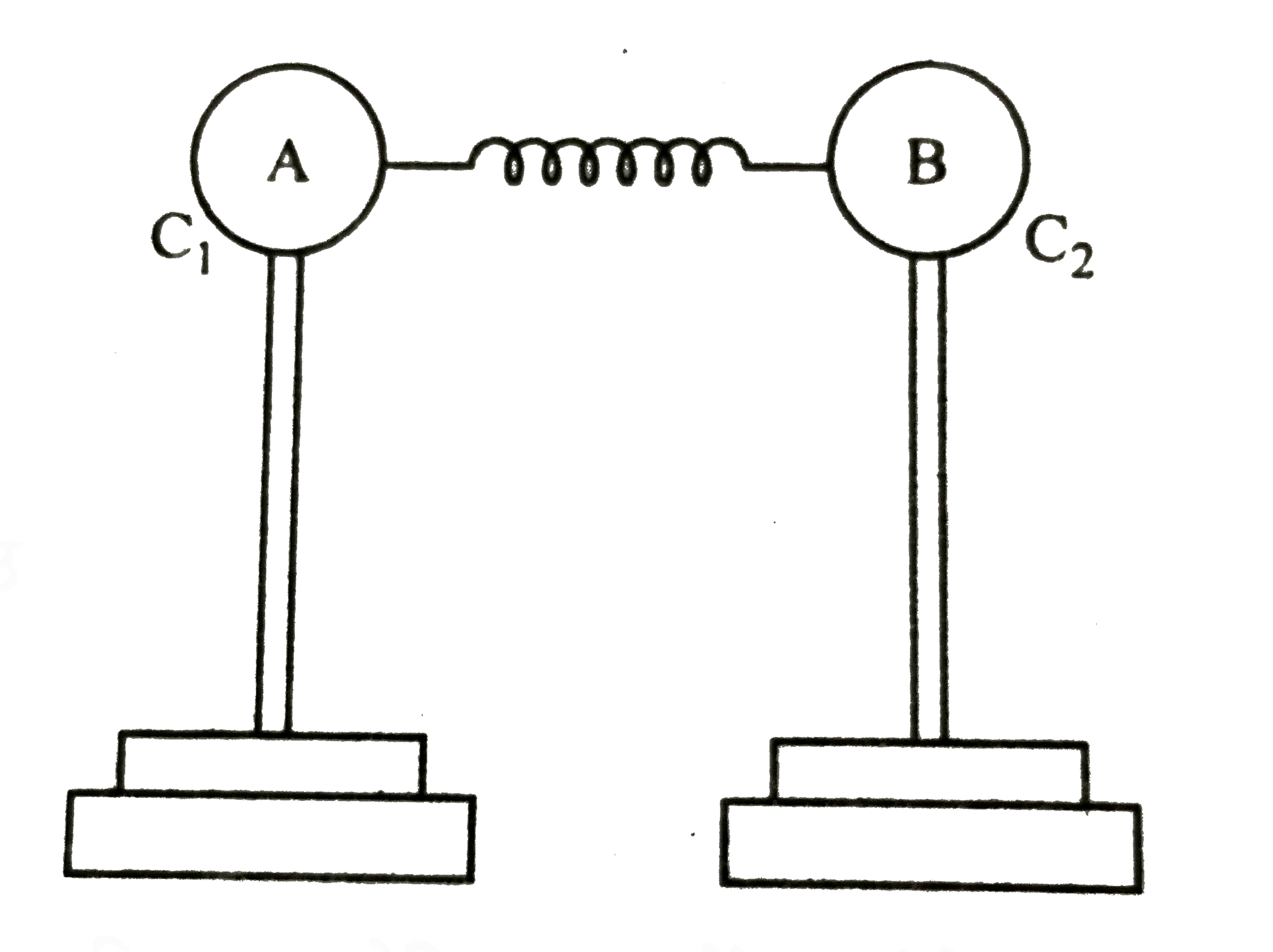
उभयनिष्ठ विभव- मानलो A और B दो विलगित चालक हैं, जिनकी धारिताएँ क्रमशः C1 or C2 है | इन चालकों को क्रमश : Q1 और Q2 आवेश देने r उनके विभव क्रमश : V1 और V2 हो जाते है
अत: कुल आवेश
Q=Q1+Q2
परन्तु Q1=C1V1 तथा C2V2
Q=C1+C2
दोनों चालकों की कुल धारिता
C=C1+C2
मानलो दोनों चालकों को तार द्वारा जोड़ने पर उनका उभयनिष्ठ विभव V हो जाता है |
अतः सूत्र Q = CV से
Q1+Q2=(C1+C2)V
या V=Q1+Q2C1+C2
या V=C1V1+C2V2C1+C2
यही उभयनिष्ठ विभव के लिए विजका है |
(ii) सयोजन में ऊर्जा हास - दोनों चालकों को जोड़ने से पलहे A और B की कुल ऊर्जा
U1=12C1V21+12C2V22
दोनों चालकों को जोड्ने के बाद A और B की कुल ऊर्जा
U2=12C1V2+12C2V2
=12(C1+C1)V2
=12(C1+C2)(C1V1+C2V2C1+C2)
=12.((C1V1+C2V2)C1+C2
∴ U1=U2=(12C1V21+12C1V22)=12.(C1V1+C2C2)2C1+C2
=12[(C1C21+C2V22)(C1+C2)−(C1V1+C2V2)2C1+C2]
=12[C1C2V21+C1C2V22−2C1C2V1V2C1+C2]
=12.C1C2C1+C2[V21+V22−2V1V2]=C1C22(C1+C2)(V1−V2)2
चुकी (V1−V2)2 धनात्मक है | अतः U1−U2 भी धनात्मक होगा | अतः आवेश के पुनर्वितरण में सैदव ऊर्जा का हास होगा है |
इस प्रकार , ऊर्जा हास =C1C22(C1+C2)(V1−V2)2
Topper's Solved these Questions
- स्थिर विद्युत विभव एवं धारिताBOOK - NAVBODHCHAPTER - स्थिर विद्युत विभव एवं धारिताEXERCISE - मूल्य आधारित प्रश्न
1 Videos
- स्थिर विद्युत विभव एवं धारिताBOOK - NAVBODHCHAPTER - स्थिर विद्युत विभव एवं धारिताEXERCISE - आंकिक प्रश्न
12 Videos
- स्थिर विद्युत विभव एवं धारिताBOOK - NAVBODHCHAPTER - स्थिर विद्युत विभव एवं धारिताEXERCISE - लघु उत्तरीय प्रश्न
37 Videos
- समतल पृष्ठ द्वारा अपवर्तन BOOK - NAVBODHCHAPTER - समतल पृष्ठ द्वारा अपवर्तन EXERCISE - आंकिक प्रश्न
5 Videos
- स्थिरवैद्युत विभव तथा धारिता BOOK - NAVBODHCHAPTER - स्थिरवैद्युत विभव तथा धारिता EXERCISE - NCERT पाठयपुष्तक के प्रश्नोत्तर
65 Videos
Similar Questions
अनिल ने नल की टोंटी खोली तो पाया कि नल में पानी नहीं आ रहा है। उसने टंकी काढक्कन खोलकर देखा तो पाया कि टंकी में पानी नहीं है। टंकी में पानी भरने के लिए उसने स्टार्टर ( Starter) का बटन दबाया किंतु मोचर चालू में पानी नहीं है| हो पाया | बिजली मिस्त्री (Technician) को बुलवाया गया। मिस्त्री ने जाँच करने के बाद बतलाया कि स्टार्टर का संधारित्र (Condenser or Capacitor) खराब हो गया है। संधारित्र बदलने पर स्टार्टर ने काम करना प्रारंभ कर दिया। उपर्युक्त गद्यांश के आधार पर निम्न प्रश्नों के उत्तर दीजिए-
(i) अनिल ने किन मूल्यों का प्रदर्शन किया ?
(ii) संधारित्र का कार्य क्या है ?
(iii) एक आवेशित संधारित्र पर कुल कितना आवेश होता है ?
(iv) एक संधारित्र की धारिता 3uF है। यदि उसे 100 V विभवांतर तक आवेशित किया जाए तो संधारित्र पर आवेश की मात्रा क्या होगी ?
View Solutionक्या 1 सैमी त्रिज्या का धातु का गोला एक कूलाम आवेश धारण कर सकता है ?
View Solutionविद्युत् विभव किसे कहते हैं ? यह अदिश राशि है या सदिश राशि।
View Solutionयदि किसी माध्यम का क्रान्तिक कोण 45∘ हों, तो माध्यम का अपवर्तनांक कितना होगा ?
View Solution5×10−8C तथा −3×10−8C के दो आवेश 16cm दुरी पर स्थित है दोनों आवेशों को मिलाने वाली रेखा के किस बिंदु पर विघुत विभव शून्य होगा? अनंत पर विभव शून्य लिखिय?
View Solutionदो आवेशित चालकों की धारिताएँ क्रमशः C1औरC2है | उन्हें Q1और Q2 आवेश देने पर उनके विभव क्रमशः V1और V2 हो जाते है | यदि उन्हें तर से जोड़ दिया जाये तो निम्न की गणना कीजिए :
(i) उभयनिष्ठ विभव (ii) संयोजन में ऊर्जा ह्रास
View Solutionयदि z1 और z2 के मापांक क्रमश: |z1| और |z2| हो, तो निम्न में से कौन-सी सही है -
View Solutionदिया है : A=(a+2,-1) और B=(11,7) a ज्ञात कीजिये यदि AB=17 हो।
View Solutionदो अनन्त लम्बाई के समान्तर तार जिन पर रेखीय आवेश घनत्व क्रमश: λ1, औरλ2 , हैं R मीटर की दूरी पर रखे हैं, उनमें से किसी एक की एकांक लम्बाई पर बल होगा
View SolutionP_4O_6 और P_4O_10 में, प्रत्येक फॉस्फोरस परमाणुओं से बंधित ऑक्सीजन परमाणुओं की संख्या क्रमश: है-
View Solution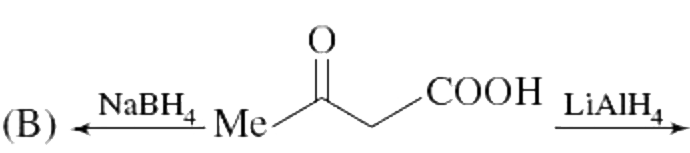 (A)
(A)
a और B क्रमश है :
View Solutionअभिक्रिया के अनुसार Br_(2(g)) के कणन पर विचार कीजिए: Br_2 (g)
View Solutionयदि I_(2)Cl_(6) में सहसंयोजक बंध और उपसहसंयोजक बंध की संख्या क्रमश: m और n है, तब m + n का योग ज्ञात कीजिए।
View Solutionयहाँ दिए गए यौगिक में,
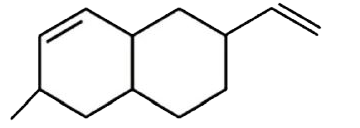 यदि X और Y क्रमश: द्वितीयक और तृतीयक C परमाणुओं की संख्या है। यहाँ x+Y के योगफल का मान ज्ञात कीजिए।
यदि X और Y क्रमश: द्वितीयक और तृतीयक C परमाणुओं की संख्या है। यहाँ x+Y के योगफल का मान ज्ञात कीजिए।
View Solutionनिम्नलिखित अभिक्रिया पर विचार कीजिए :
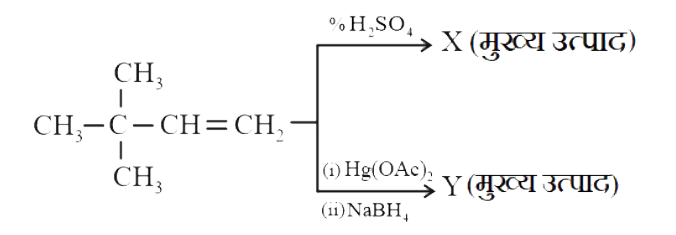
[X] और [Y] क्रमश: हैं
View Solutionयदि A और B के दो अणुओं का द्रव्यमान क्रमश: 100 amu और 64 amu है और A की विसरण दर 12xx10^(-3) है, तो B की विसरण दर क्या होगी?
View Solution
