निम्न कथन पर विचार करें ।
सीधी रेखाओं के एक ऐसे युग्म का अस्तित्व हैं , जो एक - दूसरे से प्रत्येक स्थान पर समदूरस्थ होती हैं । क्या यह कथन यूक्लिड की पाँचवीं अभिधारणा का एक प्रत्यक्ष (सीधा ) परिणाम हैं ? स्पष्ट कीजिए ।
एक रेखा l लिया और एक बिंदु P ऐसा लिया जो इस रेखा l पर स्थित नहीं हो । अब , प्लेफेयर अभिगृहीत से (जो यूक्लिड की पाँचवीं अभिधारणा के समतुल्य हैं ) हम जानते हैं कि P से होकर जाती हुई एक अव्दितीय रेखा m होती हैं जो l के समान्तर हैं ।
अब , एक बिंदु की एक रेखा से दूरी उस बिंदु से रेखा पर डाले गए लम्ब की लम्बाई होती हैं । m पर स्थित किसी बिंदु से रेखा l की दूरी और l पर स्थित किसी बिंदु से रेखा m की दूरी सदैव समान होगी । अतः ये दोनों रेखाएँ l और m प्रत्येक स्थान पर एक - दूसरे से समदूरस्थ हैं ।
Topper's Solved these Questions
- यूक्लिड की ज्यामितीय का परिचय BOOK - KC SINHACHAPTER - यूक्लिड की ज्यामितीय का परिचय EXERCISE - अभ्यास 7.1 (अतिलघु उत्तरीय प्रश्न )
5 Videos
- यूक्लिड की ज्यामितीय का परिचय BOOK - KC SINHACHAPTER - यूक्लिड की ज्यामितीय का परिचय EXERCISE - अभ्यास 7.1 (लघु उत्तरीय प्रश्न)
7 Videos
- बीजीय सर्वसमिकाएँBOOK - KC SINHACHAPTER - बीजीय सर्वसमिकाएँEXERCISE - वस्तुनिष्ठ प्रश्न
18 Videos
- रेखाएं और कोणBOOK - KC SINHACHAPTER - रेखाएं और कोणEXERCISE - वस्तुनिष्ठ प्रश्न
9 Videos
Similar Questions
एक ऐसे बिंदु का अस्तित्व है जिससे कोई रेखा नहीं गुजर सकती हैं ।
यह कथन सत्य हैं या असत्य । अपने उत्तरों के लिए कारण दें ।
View Solutionअधिगृहीत और अवधारणा से आप क्या समझते हैं ?
View Solution4x2+9+12xके गुणनखंड निम्नलिखित में कौन है ?
View Solutionबगल के चित्र में x बराबर है
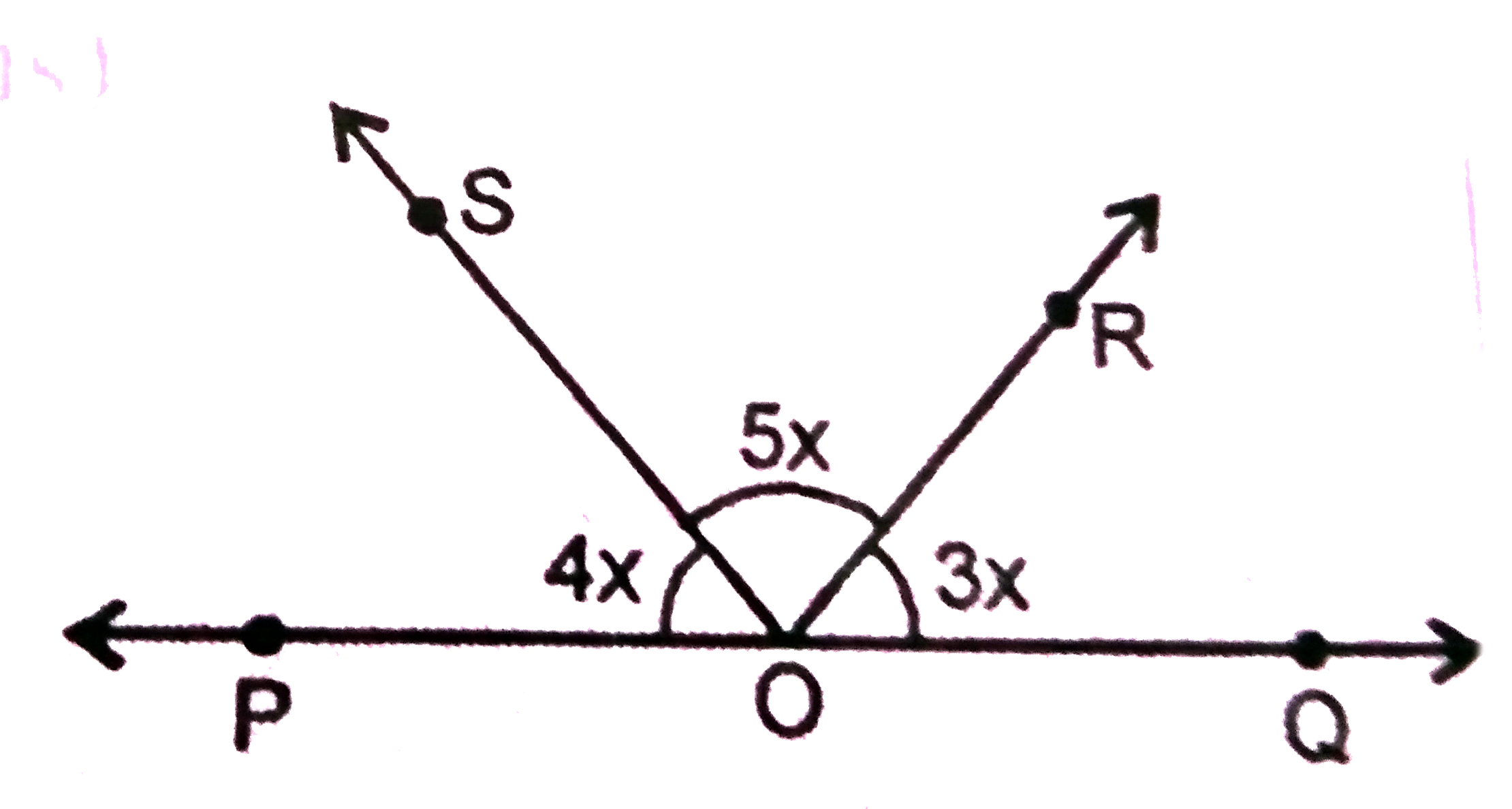
View Solutionऑक्सीकरण अवस्था के 'अयमानुपात का क्या अर्थ हैं? एक उदाहरण दीजिये|
View Solutionएक ही कोटि की दो वर्ग आव्यूहों A तथा B पर विचार कीजिये। निम्न में से कौन-सा कथन सत्य है-
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionयदि एक कण पर क्रिया करते हुए तीन बल संतुलन में हैं। पहले दो के बीच का कोण 90∘, ... दूसरे और तीसरे के बीच का कोण 120∘ हैं, तो बलों का अनुपात ज्ञात कीजिए।
View Solutionनिम्नलिखित प्रश्नों के उत्तर प्रत्येक लगभग 20 शब्दों में लिखिए: $ काशी में बाबा विश्वनाथ और बिस्मिल्ला खाँ एक-दूसरे के पूरक हैं - कथन का क्या आशय है?
View Solutionएक समबहुभुज के प्रत्येक बहिष्कोण की माप ज्ञात कीजिए जिसकी
5 भुजाएँ हैं,
View Solutionएक समबहुभुज के प्रत्येक बहिष्कोण की माप ज्ञात कीजिए जिसकी
12 भुजाएँ हैं।
View Solutionआँकड़ों का प्रबंधन #!#आँकड़े क्या हैं ? #!#एक परिचय
View Solutionज्योतिबा फुले के रचनाकार सुधा अरोड़ा मूलतः एक पर हैं।
View Solutionविश्व की सभी भाषाएँ थोड़े से फेरबदल से एक ही लिपि में लिखी जा सकती हैं।' यह कथन
View Solutionनिम्नलिखित यौगिक (A) पर विचार कीजिए। सही कथन का चयन कीजिए।
View Solutionघन आधारित एकक कोष्ठिका में कितने परमाणु हैं, जिसके प्रत्येक कोने पर एक परमाणु है और घन के प्रत्येक काय विकर्ण पर दो परमाणु हैं?
View Solution
