Question

रैखिक प्रोग्रामिंग इष्टतम मान (अधिकतम या न्यूनतम) को खोजने की एक विधि है जब संबंध रैखिक समीकरणों या असमानताओं के रूप में व्यक्त किया जाता है।

उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए।
निम्नलिखित रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल करें।
$z=8x+7y$
निम्नलिखित व्यवरोध है
$3x+y\le 66$
$x+y\le 45$
$x\le 20$
$y\le 40$
$x,y\ge 0$
$\left(i\right)$ $z=8x+7y$ का अधिकतम मान क्या होगा
$\left(ii\right)$ $z=8x+7y$ का न्यूनतम मान क्या होगा

Options

A. `(i)325.5`
`(ii)0`
B. `(i)325.5`
`(ii)160`
C. `(i)325.5`
`(ii)202`
D. `(i)325.5`
`(ii)320`

Answer

A

Explanation

हम सर्वप्रम निम्नलिखित रेखाओं के आलेख खींचते हैं।
`3x+y=66`…………1
`x+y=45`……….2
`x=20`………3
`y=40`……4
सुसंगत क्षेत्र, क्षेत्र `OEPQRGO` है जो स्पष्टतः परिबद्ध है।

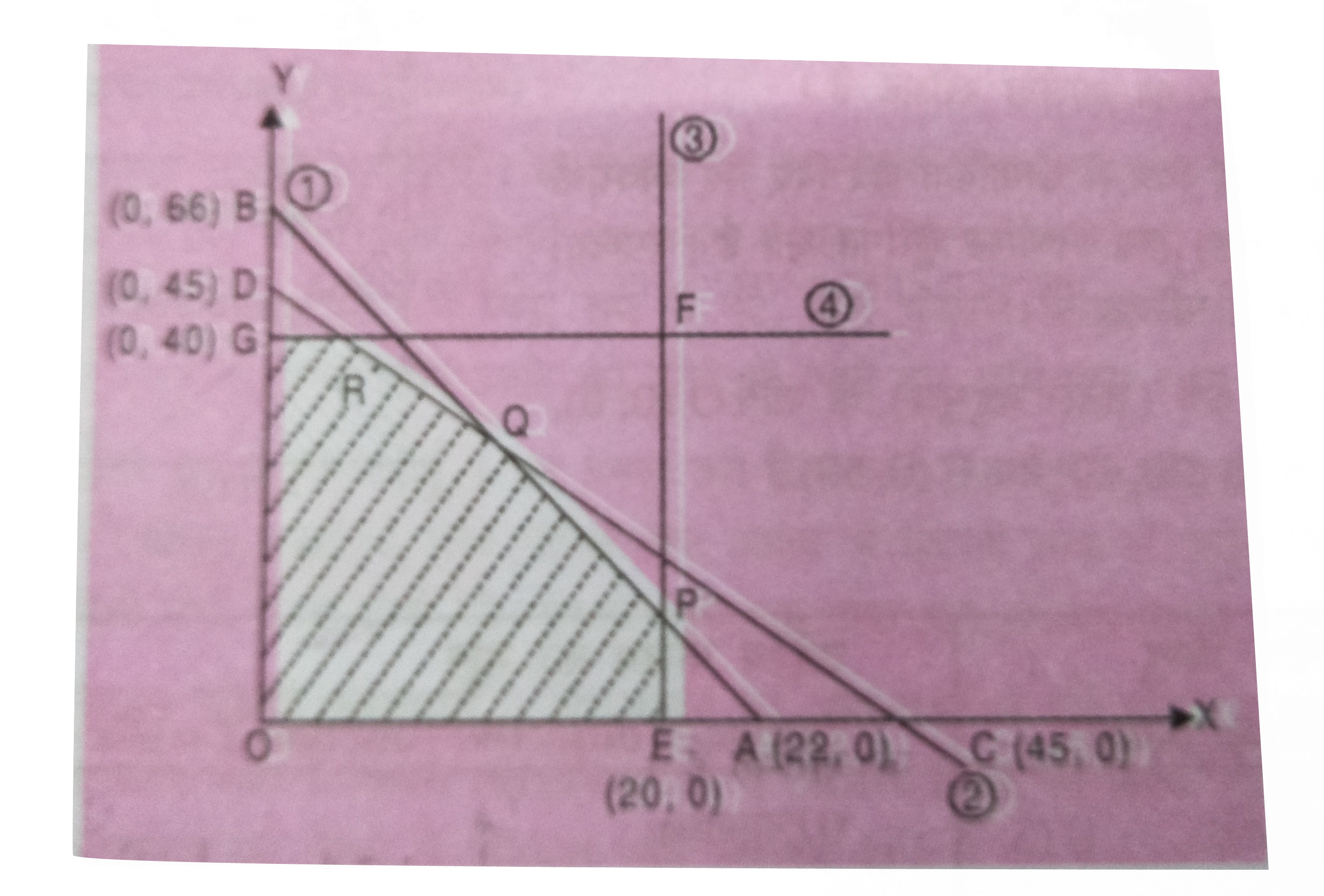
सुसंगत क्षेत्र O E P Q R G के शीर्ष
`O(0,0),E(20,0),P(20,6),Q(21/2,69/2),R(5,40)` तथा `G(0,40)` है।
दिया है `z=8x+7y`
`O(0,0)` पर `z=0`
`E(20,0), पर ,z=160`
`P(20,6)`, पर `,z=202`
`Q(21/2,69/2)`, पर `z=325.5`
`R(5,40),` पर ,`z=320`
`G(0,40),` पर `,z=280`
स्पष्टतः `Q(21/2,69/2)` पर z अधिकतम है तथा यह अधिकतम मान 325.5 है।