5x+2y का महत्तम तथा न्यूनतम मान ज्ञात करें जबकि
−2x−3y≤−6 अर्थात 2x+3y≥6,x−2y≤2,
6x+4y≤24,−3x+2y≤3
x≥0 तथा y≥0
माना कि z=5x+2y
सर्वप्रथम हम निम्नलिखित रेखाओं का आलेख खींचते है।
2x+3y=6,x−2y=2,6x+4y=24 तथा −3x+2y=3
छायांकित क्षेत्र ABCD सुसंगत क्षेत्र है।
स्पष्टतः सुसंगत क्षेत्र परिमित (परिबद्ध) है।
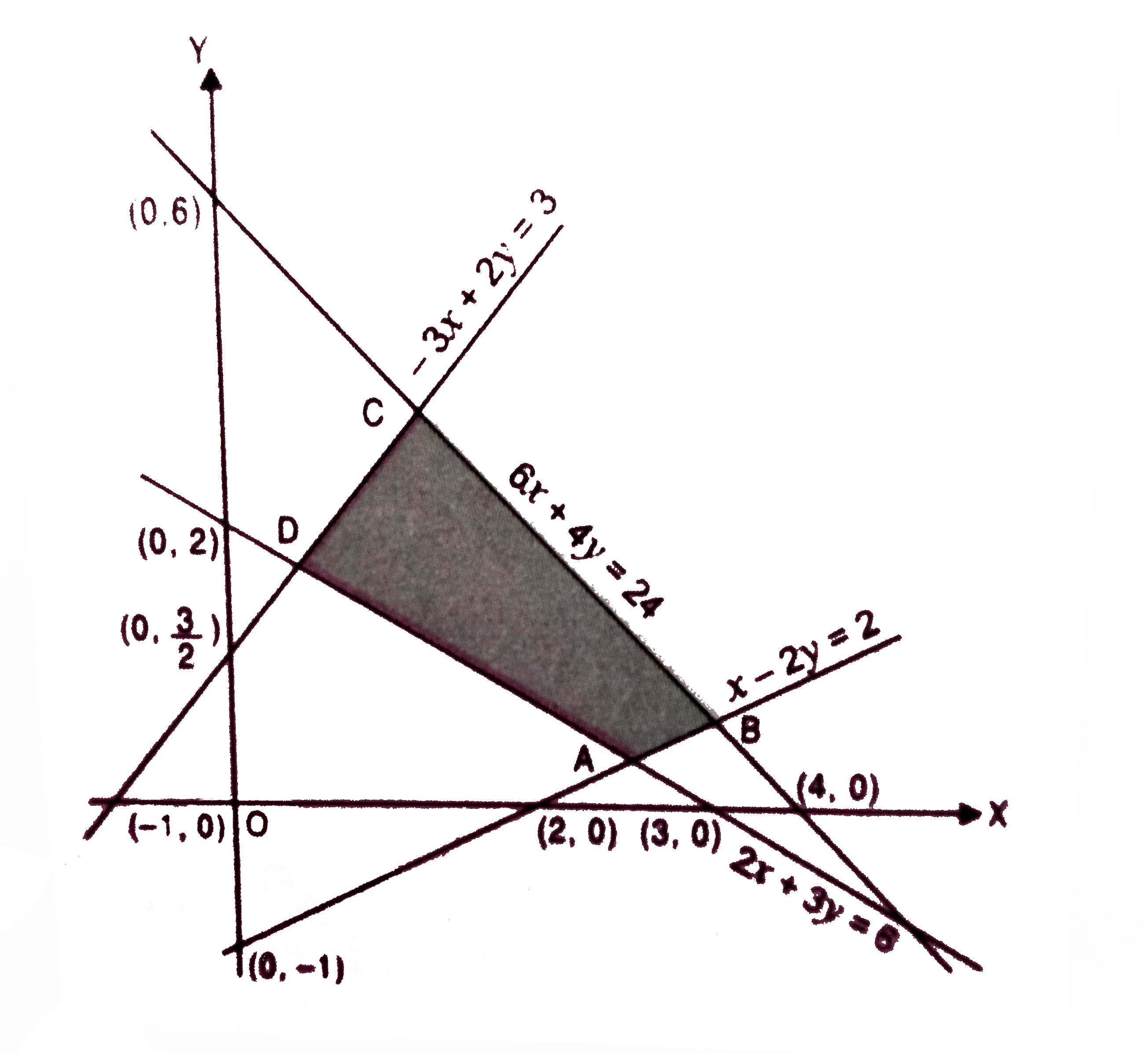
सुसंगत क्षेत्र का शीर्ष A(187,27),B(72,34),C(32,154) तथा D(313,2413) हैं।
ये बिंदुएं संगत प्रतिच्छेदी रेखाओं को हल करने से प्राप्त हुए है।
दिया है z=5x+2y
A(187,27) पर,z=947
B(72,34) पर,z=19
C(32,154) पर,z=15
D(313,2413) पर ,z=6313
स्पष्टतः Z का अधिकतम मान शीर्ष B पर है तथा न्यूनतम मान शीर्ष D पर हैं। Z का अधिकतम मान 19 है तथा न्यूनतमत मान 6313 है।
Second method: माना कि 5x+2y=P
हम सुसंगत क्षेत्र में एक उपयुक्त बिंदु A(187,27) लेते हैं।
5x+2y=P,x=187 तथा y=27 रखने पर हमें मिलता है P=947
हम सरल रेखा 5x+2y=947 खींचते है।
स्पष्टतः यह रेखा A से गुजरती है।
अब इस रेखा के समांतर रेखाएं (जिन्हें रेखाएं कहते हैं) खींचते हैं । इस तरह की रेखाएं बहुभुज ABCD से घिरे सुसंगत क्षेत्र को काटती है जब तक यह शीर्ष B पर नहीं पहुंचता है।
अतः शीर्ष B(72,34) अधिकतम मान देगा।
∴z का महत्तम मान =5×72+2×34=19
उसी तरह रेखा 5x+2y=947 को अपने आप के समांतर नीचे लाने पर हमें मूल बिंदु से न्यूनतम दूरी पर एक रेखा मिलती है जिसका कम से कम एक बिंदु feasible region में है। यह रेखा बिंदु D(313,2413) से जाती है।
यह बिंदु z का न्यूनतम मान देता है
z का न्यूनतम मान =5×313+2×2412=6313=4.85
Topper's Solved these Questions
- रैखिक प्रोग्रामनBOOK - KC SINHACHAPTER - रैखिक प्रोग्रामनEXERCISE - दो चरों में एक रैखिक असमिका के हल पर आधारित प्रश्नः
4 Videos
- रैखिक प्रोग्रामनBOOK - KC SINHACHAPTER - रैखिक प्रोग्रामनEXERCISE - दो चरों में रैखिक असमिकाओं के निकाय के हल पर आधारित प्रश्नः
4 Videos
- यादृच्छिक चर और प्रायिकता बंटन BOOK - KC SINHACHAPTER - यादृच्छिक चर और प्रायिकता बंटन EXERCISE - Objective Questions
4 Videos
- रैखिक समीकरणों के निकाय का हल BOOK - KC SINHACHAPTER - रैखिक समीकरणों के निकाय का हल EXERCISE - Objective Questions
4 Videos
Similar Questions
निम्नलिखित रैखिक असमिकाओं को आलेखीय विधि से हल करें:
3x−4y<12
View Solutionनिम्नलिखित रैखिक असमिकाओं के निकाय को आलेखीय विधि से हल करें।
3x+4y≤60,x+3y≤30,x≥0,y≥0
View Solutionएक यादृच्छिक चर X का बंटन नियम निम्नलिखित है :
x234P(X=x)0.30.40.3
इस बंटन का मानक विचलन ज्ञात करें।
View SolutionFor the system of equations :
a1x+b1y+c1z=0,a2x+b2y+c2z=0,a3x+b3y+c3z=0
if ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=0, then this system has:
View Solution2x+y−3≥0,x−2y+1≤0,x≥0,y≥0
View Solutionहल कीजिए - x+2y≥2,3x+y≥3,4x+3y≥6,x≥0,y≥0
View SolutionExhibit graphically the solution set of the following system of linear inequations:
x−2y≤2,x+y≥3,−2x+y≤4,x≥0,y≥0
View Solutionनिम्न असमिका निकाय को आलेखीय विधि हल कीजिए
2x+3y≥6,x+9y≤4,x≥0 और y≥0.
View SolutionMinimize and Maximize z=5x+2y subject to constrains −2x−3y≤−6,x−2y≤2,3x+2y≤12,−3x+2y≤3 and x,y≥0
View Solution1+cosec2x का न्यूनतम मान ज्ञात कीजिए।
View Solutionयदि xy = 4 तथा x> 0 तो x का वह मान ज्ञात कीजिए जिसके लिए x + y न्यूनतम है।
View Solutionअधिकतम करो, Z=2x+5y
प्रतिबन्ध, x+4yle24
3x+yle21
x+yle9
ऋणेत्तर प्रतिबन्ध xge0,yge0
View Solutionअधिकतम और न्यूनतम मान ज्ञात कीजिये
यदि Z=5x+2y
प्रतिबन्ध 2x+3Yle6
x-3yle3
3x+4yle24
-3x+2yle3
ऋणेत्तर प्रतिबन्ध xge0,yge0
View Solutionन्यूनतम करो z=200x+500y
प्रतिबन्ध x+2y>10
3x+4yle24
ऋणेत्तर प्रतिबन्ध xge0,yge0
View Solutionन्यूनतम करो z=3x+2y
प्रतिबन्ध 2x+y≥8
x+2y≥10
5x+7y≤38
ऋणेत्तर प्रतिबन्ध x≥0,y≥0
View Solution
