Question

एक बीमार व्यक्ति के लिए एक आहार से कम-से-कम विटामिन की $4000$ इकाइयां , खनिज की $50$ इकाइयां और कैलोरीज की $1400$ इकाइयां होनी चाहिए दो भोज्य $A$ और $B$ उपलब्ध है जिनकी कीमत क्रमशः $4$ रू और $3$ रू प्रति इकाई है यदि $A$ की एक इकाई में $200$ विटामिन की इकाई $1$ खनिज की इकाई और $40$ कैलोरीज की इकाई हो एवं $B$ की एक इकाई में $100$ विटामिन की इकाई $2$ खनिज की इकाई और $40$ कैलोरीज की इकाई हो तो ज्ञात करें की भोज्यों का कैसा सम्मिश्र किया जाए की आवश्यक तत्वों को पूरा करते हुए मूल्य न्यूनतम हो ?

Options

A. `110`
B. `120`
C. `130`
D. `140`

Answer

A

Explanation

दिए गए आंकड़ों को निम्नलिखित सारणी में दिखाया गया है:

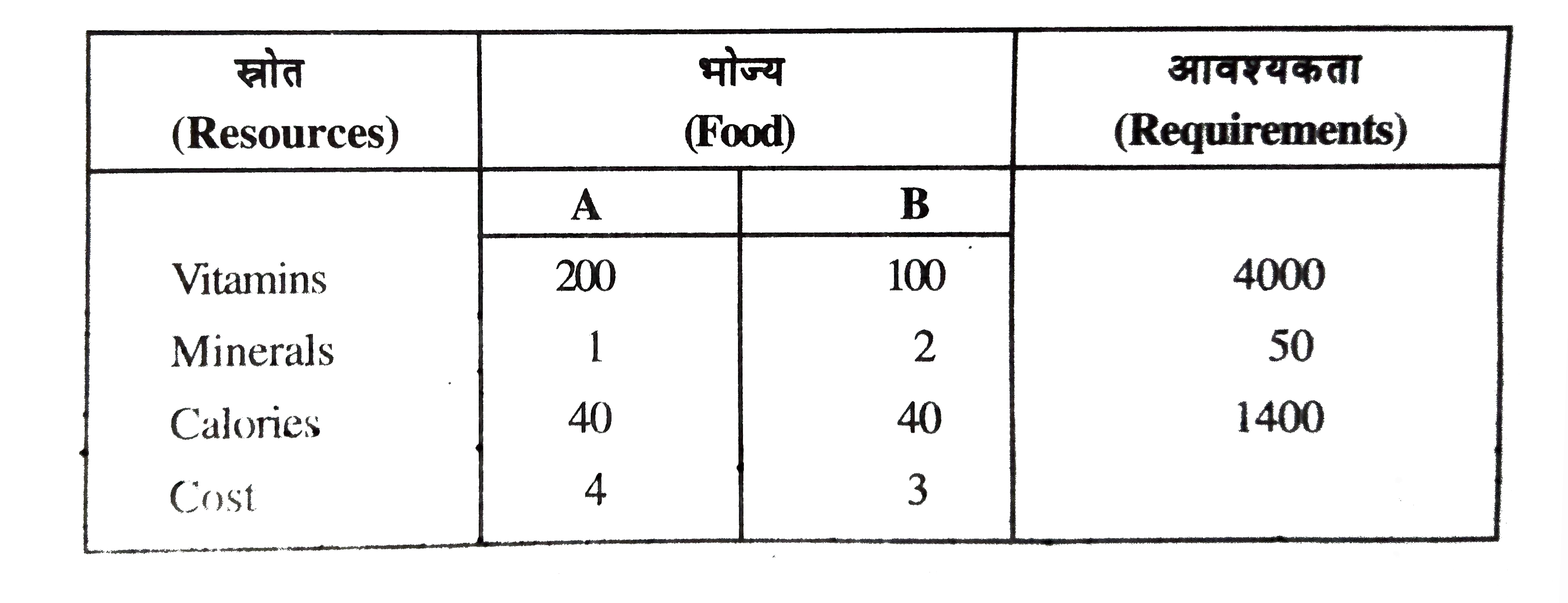
माना कि भोज्य A का x तथा भोज्य B का y इकाई मिश्रित किया जाता है।
तो कुल खर्च `z=4x+3y` (रू0)
स्पष्टतः `xge0,yge0`
चूंकि आहार में कम से कम 4000 इकाई विटामिन होना चाहिए।
`:.200x+100yge4000` या `2x+yge40`
उसी तरह चूंकि आहार में न्यूनतम 50 इकाई खनिज होना चाहिए।
`:.x+2yge50`
पुनः चूंकि आहार में न्यूनतम 1400 कैलोकरी होना चाहिए।
`:.40x+40yge1400` अर्थात `x+yge35`
अतः रैखिक प्रोग्रामन समस्या का गणितीय रूप निम्नलिखित होगा:
न्यूनतमीकरण करें `z=4x+3y`
जबकि
`2x+yge40`
`x+2yge50`
`x+yge35`
`xge0,yge0`
अब हम निम्नलिखित रेखाओं का आलेख खींचते हैं।
`2x+y=40,x+2y=50,x+y=35`
छायांकित क्षेत्र सुसंगत क्षेत्र है जो कि स्पष्टतः अपरिबद्ध है।
सुसंगत क्षेत्र का शीर्ष `A(50,0),B(20,15),C(5,30)` तथा `D(0,40)` है।
`:’z=4x+3y`
`:.A(50,0),` पर,`z=4xx50=200`
`B(20,15)` पर,`z=4xx20+3xx15=125`
`C(5,30)` पर,`z=4xx5+3xx30=110`
`D(0,40)` पर,`z=3xx40=120`
बिंदु `C(5,30)` पर z का मान न्यूनतम है। z के न्यूनतम मान के लिए भोजय X का 5 इकाई तथा भोज्य Y का 30 इकाई मिश्रित करना चाहिए।