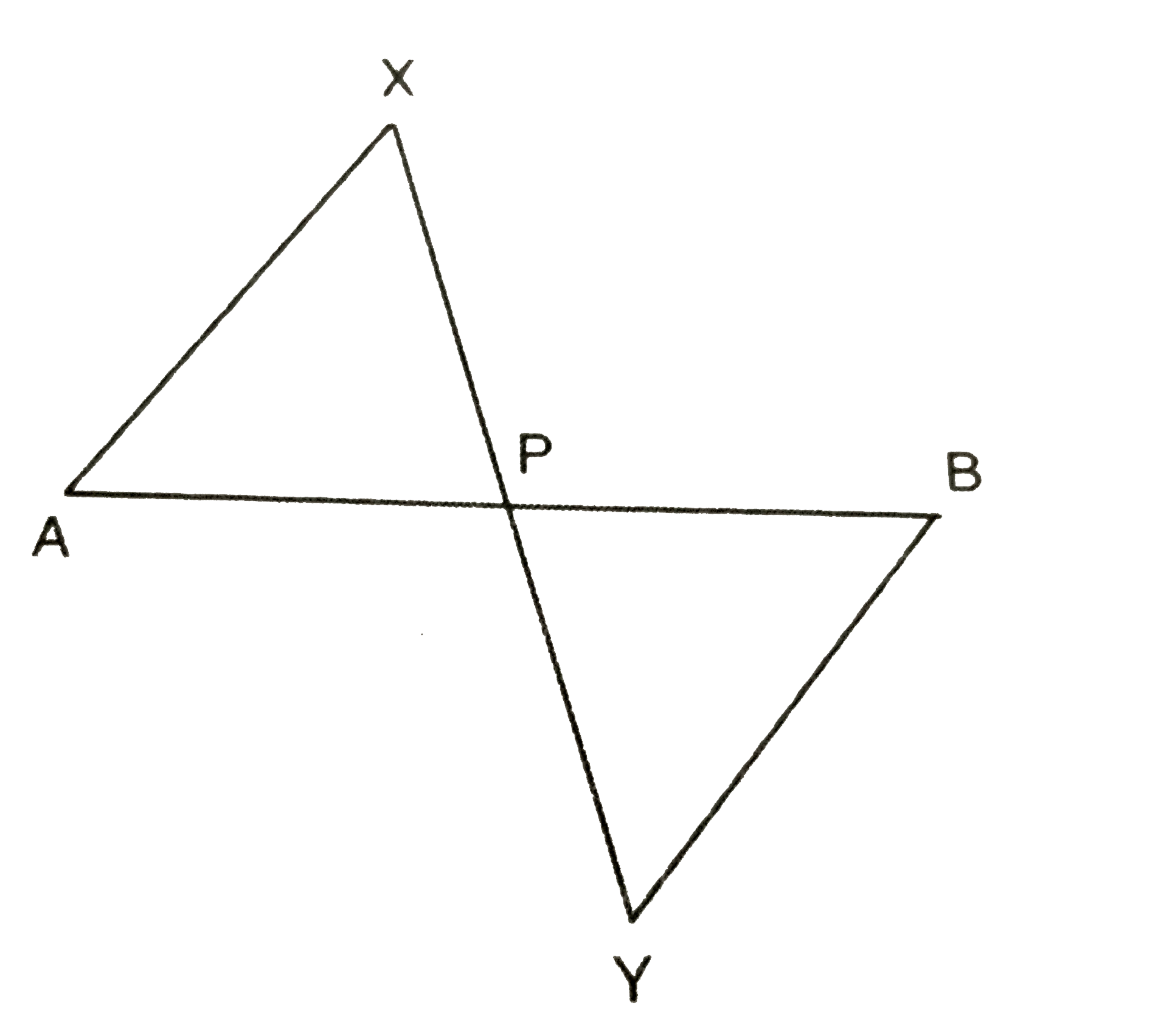
अब एक रेखाखण्ड है जिसके विपरीत दिशाओं में दो बराबर रेखाखण्ड AX तथा BY इस प्रकार खींचे गये हैं कि AX || BY,यदि AB और XY एक दूसरे को बिन्दु P पर प्रतिच्छेदित करते हैं, तो सिद्ध कीजिए कि
(i)ΔAPX≅ΔBPY
(ii)AB और XY एक दूसरे को समद्विभाजित करते हैं |
चूँकि AX || BY और तिर्यक रेखा अब उन्हें क्रमशः A और BY पर प्रतिच्छेदित करती है |
∴ ∠BAX=∠ABY [एकान्तर कोण]
इसी प्रकार, ∠AXY=∠BYX [∵तिर्यक रेखा XY, समांतर रेखाओ AX तथा BY को क्रमशः X तथा Y पर काटती है ]
अब त्रिभुजों PAX तथा ΔPBYमें
∠PAX=∠PBY
∠AXP=∠BPY
तथा, AX=BY [दिया है]
अतः कोण-भुजा कोण सर्वागसमता कसौटी से
ΔPAX≅ΔBPY
⇒ AP=BPतथा PX=PY
अतः ΔAPX≅ΔBPYऔर AB तथा XY एक दूसरे को समद्विभाजित करते हैं |
Topper's Solved these Questions
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - प्रश्नावली 10.1
13 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - प्रश्नावली 10.2
3 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
20 Videos
- सांखि्यिकीय आँकड़ों का सारणीयनBOOK - RD SHARMACHAPTER - सांखि्यिकीय आँकड़ों का सारणीयनEXERCISE - बहु विकल्पीय प्रश्न
10 Videos
Similar Questions
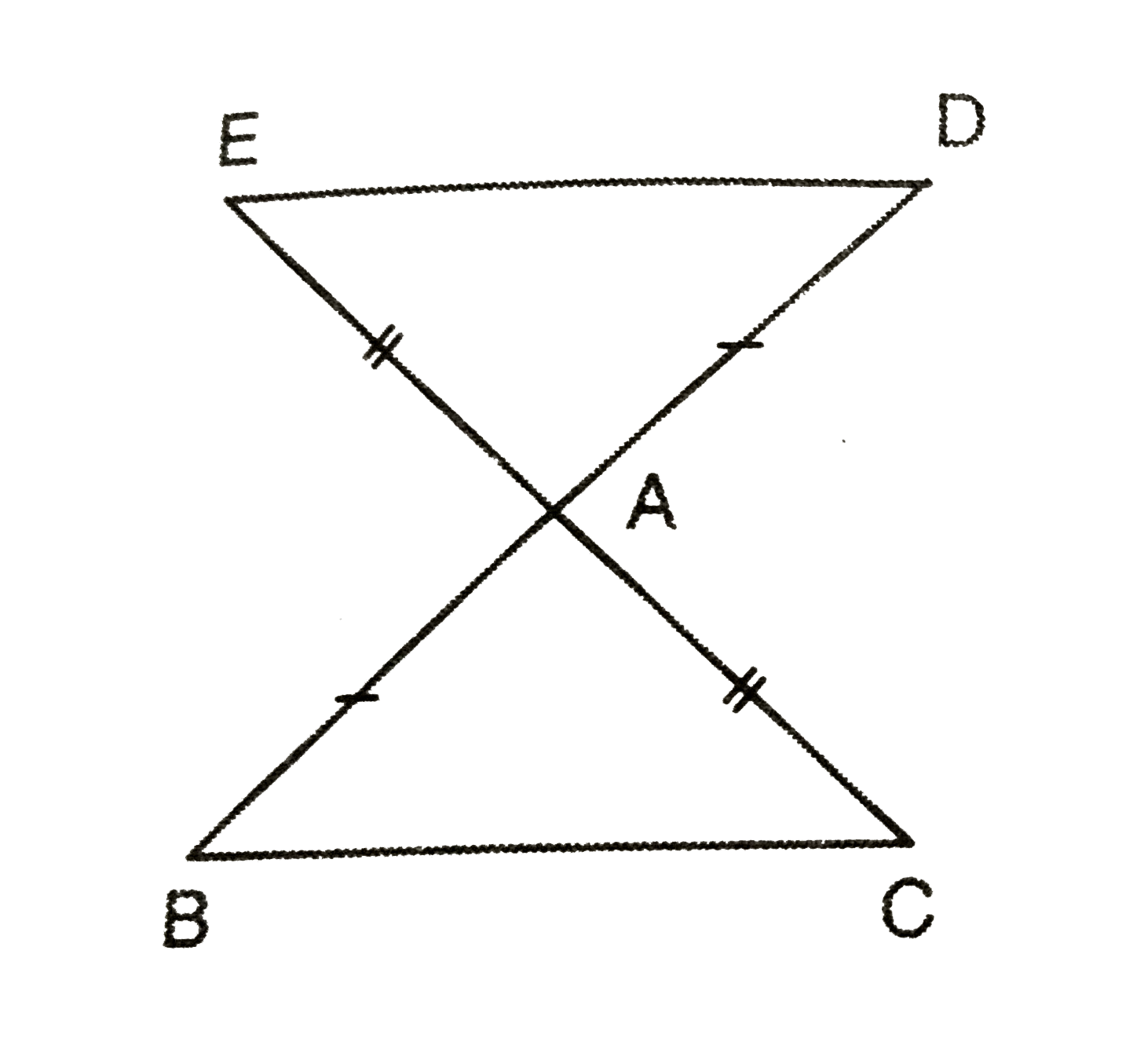
भुजाएँ BA तथा CA तथा इस प्रकार बढ़ाई गई कि BA=AD तथा CA=AE हैं | सिध्द कीजिए कि रेखाखण्ड DE∣∣BC है |
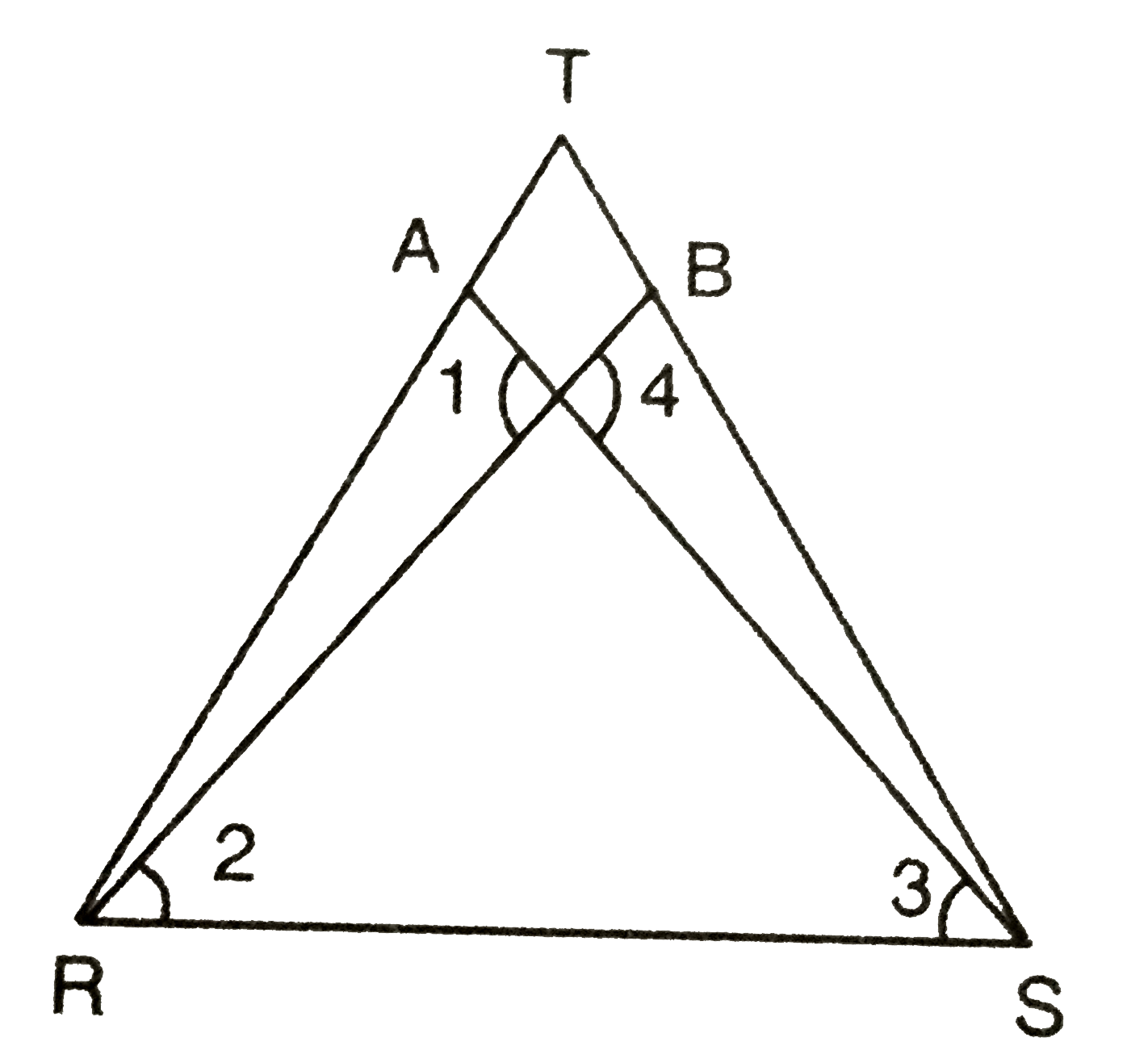
View Solutionयह दिया है RT=TS ∠1=2√3 तथा ∠4=2Sqrt(3)तो, दर्शाइए कि ΔRBT≅ΔSAT
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionप्रेक्षणो के सग्रह में से उच्चतम एव न्यूनतम प्रेक्षणो के अन्तर को कहते है ?
View Solutionयदि ¯a और ¯b दो सदिश इस प्रकार हैं कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b लंबवत होगा b पर ।
View Solutionसिद्ध कीजिए कि सरल रेखाएँ x=mz+a,y=nz+b और x=m'z+a',y=n'z+b' एक-दूसरे को काटेंगी यदि (a−a')(n−n')=(b−b')(m−m') हो।
View Solutionयदि दो वृतो की त्रिज्याएँ क्रमशः r1 व r2 है और वे एक - दूसरे को बाह्यतः स्पर्शः करते हो , तो -
View Solutionदो वृत्त एक -दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ कि संख्या लिखिए।
View Solutionसदिशों के प्रयोग द्वार सिद्ध कीजिए कि बिंदु A(−2,3,5),B(7,0,−1),C(−3,−2,−5) और D(3,4,7) इस प्रकार हैं कि AB और CD बिंदु P(1,2,3) पर प्रतिच्छेद करते हैं।
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionकिसी ΔOAB में ∠AOB=90∘ तथा बिन्दु P, Q भुजा AB को समत्रिभाजित करते हैं | सिद्ध कीजिए कि, OP2+OQ2=59AB2.
View Solutionयदि A और B दो वर्ग आव्यूह इस प्रकार हैं कि AB = A और BA = B तो सिद्ध करो कि A और B समशम होंगे |
View Solution8.8cm लम्बा एक रेखाखण्ड AB खींचिए। A को केंद्र मानकर 4 त्रिज्या का एक वृत्त तथा 3 को केंद्र लेकर त्रिज्या का एक अन्य वृत्त खींचिए। प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रतेखाओ कि रचना कीजिए।
View Solutionसिद्ध कीजिए कि एक पासो के जोड़े को फेंकने पर पहले पर 5 आना , दूसरे पास पर 6 आने कि स्वतन्त्र घटनाएँ है।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionयदि एक सममित आव्यूह A तथा एक विषम सममित आव्यूह B इस प्रकार है कि A+B=[235−1] तो AB बराबर है
View Solution
