चित्र में, ABCD एक चतुर्भुजाकार मैदान है जिसकी भुजाये चित्र में प्रदर्शित की गई है। यदि ∠DAB=90∘ हो, तो मैदान का क्षेत्रफल ज्ञात कीजिए।
स्पष्टतः ΔDAB एक समकोण त्रिभुज है |
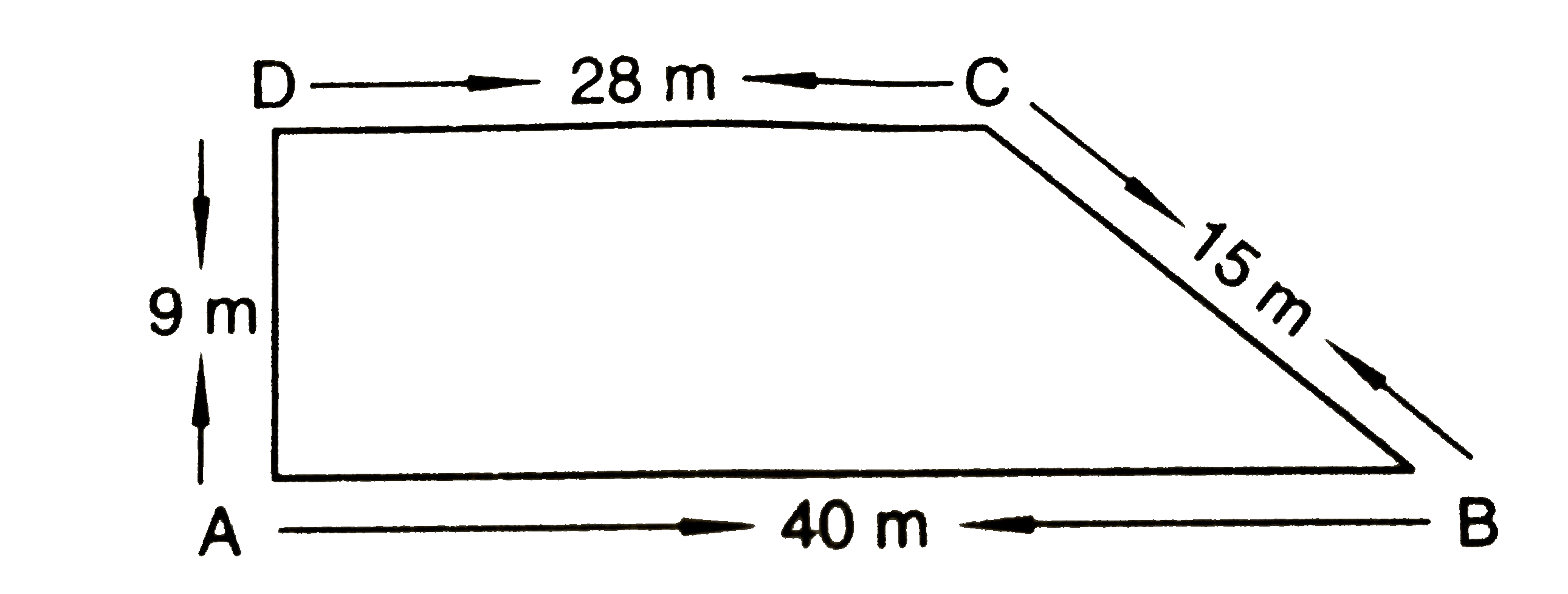
∴DB2=DA2+AB2 [पाइथागोरस प्रमेय के उपयोग से ]
⇒DB2=92+402
⇒DB=√81+1600 मी. = 41 मी.
त्रिभुज DAB में,
2s=DA+AB+BD=(9+40+41)=90 मी.
⇒s=45 मी.
⇒A1=ΔDAB का क्षेत्रफल = √45×(45−9)×(45−40)×(45−41) मी. 2
⇒A1=ΔDAB का क्षेत्रफल = √45×36×5×4 मी. 2
⇒A1=ΔDAB का क्षेत्रफल = √5×9×36×5×4 मी. 2 = √52×32×62×22 मी 2
⇒A1=ΔDAB का क्षेत्रफल = (5×3×6×2) मी. 2 = 180 मी. 2
त्रिभुज DCB में,
2s=DC+CB+BD⇒20s=28+15+41=84⇒s=42
∴A2=ΔDCB का क्षेत्रफल = √42×(42−28)×(42−15)×(42−41) मी .2
⇒A2=ΔDCB का क्षेत्रफल = √42×14×27×1 मी. 2
⇒A2=ΔDCB का क्षेत्रफल = √7×2×3×7×2×3×3×3 मी. 2
⇒A2=ΔDCB का क्षेत्रफल (7×2×3)2 मी2 = 126 मी2
अतः मैदान का क्षेत्रफल = A1+A2=(180+126)मी. 2=306 मी.2
Topper's Solved these Questions
Similar Questions
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिये जिसकी भुजाएँ 150 सेमी., 120 सेमी. तथा 200 सेमी. है।
03:11View Solutionचतुर्भुज ABCD का क्षेत्रफल ज्ञात किजीये जिसमे AB =3 सेमी. BC = 4 सेमी. CD = 4 सेमी. DA = 5 सेमी.तथा AC = 5 सेमी. |
02:16View Solutionचित्र में, त्रिभुज ABC में ∠A समकोण है तथा AL भुजा BC पर लम्ब है । सिद्ध कीजिए कि ∠BAL=∠ACB है ।
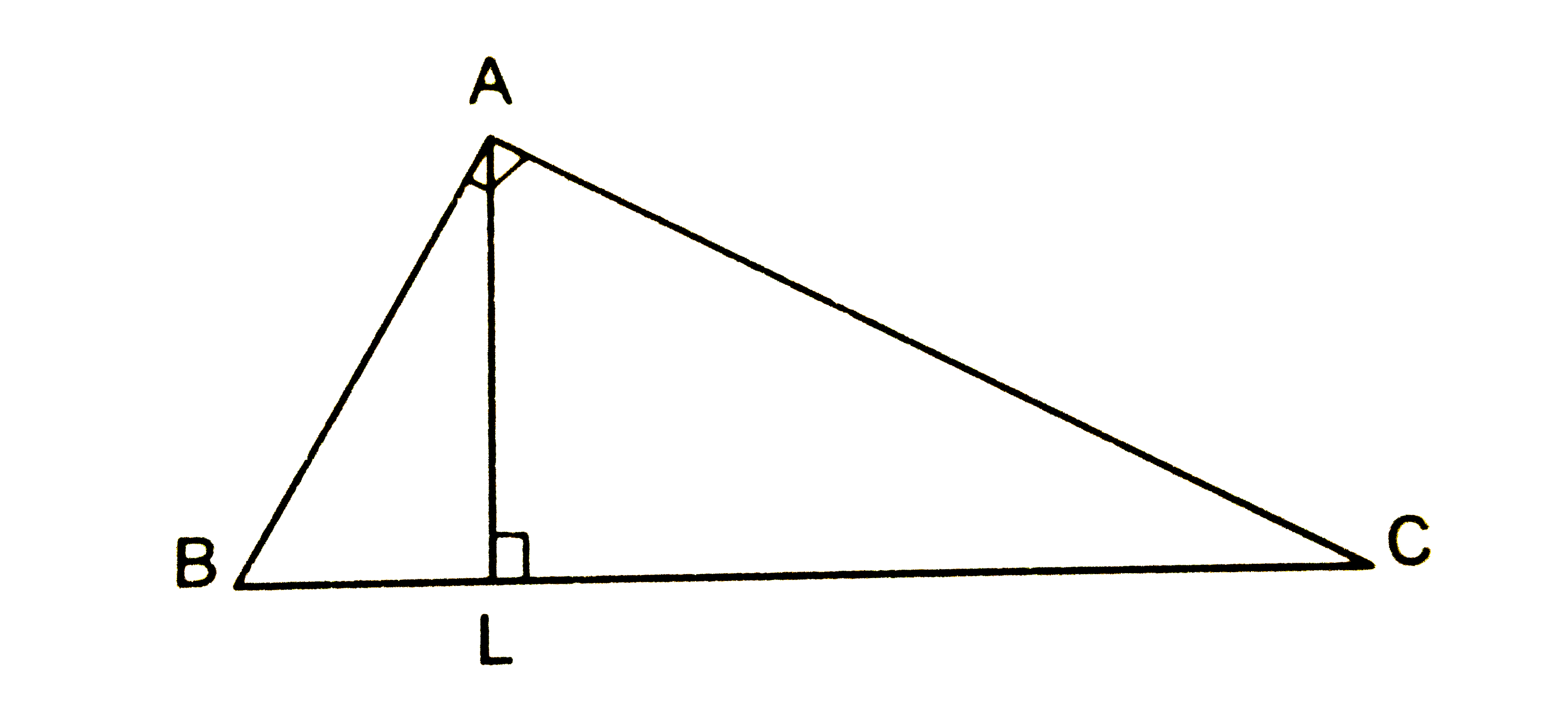 01:24View Solution
01:24View Solutionदी गई आकृति में △ABC का बहिर्वृत्त भुजाओ को Q ,P एवं R पर स्पर्श करता है। यदि AQ=8 सेमी हो तो △ABC का परिमाप ज्ञात कीजिए।
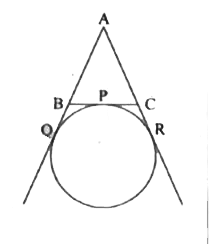 01:33View Solution
01:33View Solutionदिये गए चित्र में,बाह्य बिंदु A से वृत्त कि दो स्पर्श AB व AC खींची गई है। ∠BAC=48∘ हो ,तो ∠ABC का मान लिखिए।
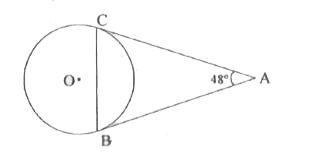 04:51View Solution
04:51View Solutionदिये गये चित्र में स्पर्श रेखा है -
 01:38View Solution
01:38View Solutionदिये गये चित्र में स्पर्श रेखाओ की संख्या है -
 01:30View Solution
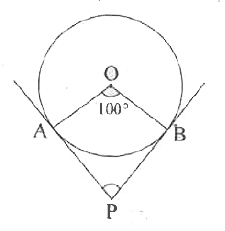
01:30View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
 04:11View Solution
04:11View Solutionदिये गये चित्र में स्पर्श रेखा है:
 02:01View Solution
02:01View Solutionदिये गये चित्र में स्पर्श रेखाओ की संख्या है:
 02:10View Solution
02:10View Solutionदिये गये चित्र में छायांकित भाग निम्न सुसंगत क्षेत्र को दर्शाता है -
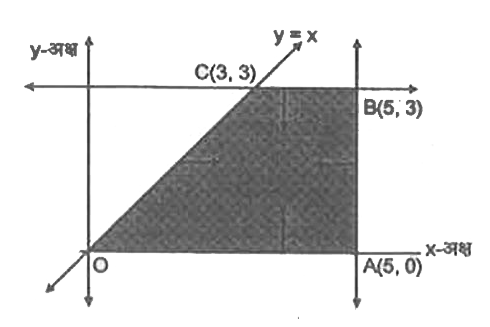
तो प्रतिबन्ध है -05:00View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
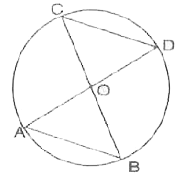
03:08View Solutionआकृति में आप को एक वृत्त C(O, r) दिया है| यदि ∠AOB=∠COD हो, तो उनकी संगत जीवाओं का अनुपात कारण देते हुए ज्ञात कीजिए |
 01:21View Solution
01:21View Solutionएक वृत्त का केंद्र (2x−1,3x+1) है। x ज्ञात कीजिए यदि वृत्त (-3,-1) में से गुजरे और व्यास की लम्बाई 20 मात्रक हो।
02:09View SolutionWhat is the area (in m2) of a triangle field whose sides measure 25 m, 39 m and 56 m?
एक त्रिभुजाकार मैदान का क्षेत्रफल (वर्ग मीटर में ) ज्ञात करें जिसकी भुजाओं का माप 25 मी, 39 मी और 56 मी है |View SolutionLength and breadth of rectangular field are in the ratio 5 : 2. If the perimeter of the field is 238 m. Find the length of the field.
एक आयताकार मैदान की लंबाई और चौड़ाई 5 : 2 के अनुपात में है। यदि मैदान का परिमाप 238 मीटर है, तो मैदान की लंबाई ज्ञात कीजिए।View Solution

