प्रदर्शित कीजिए की वर्ग की भुजाओं के मध्य-बिन्दूओं को मिलाने से प्राप्त चतुभुर्ज है भी एक वर्ग होता है।
एक वर्ग ABCD जिसमे भुजाओं AB,BC,CD,DA के मध्य-बिन्दु क्रमशः P,Q,R,S है। PQ,QR,RS तथा SP को मिलाया गया है।
सिद्ध करना है: PQRS एक वर्ग है।
रचना AC तथा BD मिलाइये।
उपपत्ति ΔABC में भुजाओं AB तथा AD के मध्य-बिन्दु क्रमशः P तथा Q है।
∴PQ∣∣AC तथा PQ=12AC ...(i)
ΔADC में भुजाओं CD तथा AD एक मध्य-बिन्दु क्रमशः R तथा S है।
∴RS∣∣AC तथा RS=12AC ...(ii)
(i) तथा (ii) से
PQ∣∣RS तथा PQ=RS ....(iii)
अतः चतुभुर्ज PQRS में सम्मुख भुजाओं का एक युग्म बराबर तथा समान्तर है।
अतः PQRS एक समान्तर चतुभुर्ज है।
∴ABCD एक वर्ग है।
∴AB=BC=CD=DA
⇒12AB=12CD तथा 12AB=12BC
⇒PB=CR तथा BQ=CQ
अतः ΔPBQ तथा ΔRCQ में
PB=RC
BQ=CQ
तथा ∠PBQ=∠RCQ [प्रत्येक कोण 90∘]
अतः भुजा-कोण-भुजा सर्वांगसमत कसौटी से
ΔPBQ≅ΔRCQ
⇒PQ=QR ...(iv)[∴ सर्वांगसम त्रिभुजों के सम्मुख भाग बराबर होते है]
(iii) तथा (iv) से
PQ=QR=RS
परन्तु PQRS एक समान्तर चतुभुर्ज है।
QR=PS
इसलिए PQ=QR=RS=PS ....(v)
अब PQ∣∣AC [(i)से]
⇒PM∣∣NO (vi)
चूँकि AB तथा AD के मध्य-बिन्दु क्रमशः P तथा S है।
∴PS∣∣BD
⇒PN∣∣MO ...(vii)
अतः PMON में
PM∣∣NO [(vi) से ]
तथा PN∣∣MO [(vii) से]
अतः PMON एक समान्तर चतुभुर्ज है।
⇒∠MPN=∠MON
⇒∠MPN=∠BOA [∴∠MON=∠BOA]
⇒∠MPN=90∘ [∴वर्ग के विकर्ण लम्ब होते है ∴AC⊥BD⇒∠BOA=90∘]
⇒QPS=90∘
अतः PQRS एक समान्तर चतुभुर्ज है इस प्रकार है की PQ=QR=RS=SP तथा ∠QPS=90∘
अतः PQRS एक वर्ग है।
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.14videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.216videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन EXERCISE - बहु विकल्पीय प्रश्न22videos
घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन
- BOOK - RD SHARMACHAPTER - त्रिभुज तथा उसके कोण EXERCISE - बहु विकल्पीय प्रश्न28videos
त्रिभुज तथा उसके कोण
Similar Questions
एक चतुभुर्ज है तीन कोण क्रमशः 110∘,50∘ तथा 40∘ है। इसका चौथा कोण ज्ञात कीजिए।
04:29View Solutionएक समान्तर चतुर्भुज के दो सम्मुख कोण (3x−2)∘ तथा (50−x)∘ है। समान्तर चतुभुर्ज के प्रत्येक कोण की माप ज्ञात कीजिए?
03:15View Solutionयदि किसी घनाभ के तीन आसन्न फलकों के क्षेत्रफल A1,A2 व A3 से दर्शाया जावे तो इस घनाभ का आयतन होगा :
04:56View Solutionयदि किसी त्रिभुज के तीनो कोण बराबर हो, तो प्रत्येक कोण का माप होगा:
04:34View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
02:33View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
01:53View Solutionपरवलय y2=4px की किसी द्विकोटि की लम्बाई 8p है। सिद्ध कीजिए कि शीर्ष को उसके सिरों से मिलाने वाली सरल रेखाएँ परस्पर लम्ब है।
03:16View Solutionएक अनभिनत पास को 6 बार उछाला जाता है। यदि एक समसंख्या प्राप्त करना एक सफलता है , तो
अधिक - से - अधिक 5 सफलताओ की प्रायिकता ज्ञात कीजिए।04:01View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?View Solutionवर्गीकृत आंकड़ों की 'से कम प्रकार' और 'से अधिक प्रकर' की संचयी बारम्बारता वक्रों के प्रतिच्छेद बिन्दु के 'भुज' से प्राप्त होता है आंकड़ों का----
View SolutionIn the given figure, ABCD is a square. EFGH is a square formed by joining mid points of sides of ABCD. LMNO is a square formed by joining mid points of sides of EFGH. A circle is inscribed inside EFGH. If area of circle is 38.5 cm2, then what is the area (in cm2) of square ABCD?
दी गई आकृति में, ABCD एक वर्ग है। ABCD की भुजाओं के केन्द्र बिन्दुओं को जोड़कर एक वर्ग EFGH बनाया गया हैं EFGH की भुजाओं के केन्द्र बिन्दुओं को जोड॒कर एक वर्ग LMNO बनाया गया है। एक वृत्त को वर्ग EFGH में अंकित किया गया हैं यदि वृत्त का क्षेत्रफल 38.5 से.मी.2 है, तो वर्ग ABCD का क्षेत्रफल (से.मी.2 में) क्या है?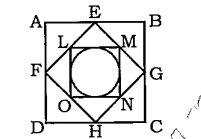
View SolutionThe area of square is 200m^2 . A new square is formed in such a way that the length of its diagonal is sqrt2 times of the given square. Then the area of the new square formed is- एक वर्ग का क्षेत्रफल 200 वर्ग मीटर है। एक नया वर्ग इस प्रकार बनाया गया है कि उसके विकर्ण की लंबाई पहले वर्ग के विकर्ण की sqrt2 गुना के बराबर है, नये वर्ग का क्षेत्रफल है-
View Solutionदोपहर का भोजन' मूलतः किस वर्ग की कहानी है ?
02:16View Solutionसमाज में वर्ग हैं, श्रेणियाँ हैं। श्रेणियों में परिवार है। समाज की एक बुनियादी इकाई परिवार भी है। समाज की अच्छाई-बुराई । परिवार के माध्यम से व्यक्त होती है। मनुष्य के चरित्र का विकास. 1 परिवार में होता है। बच्चे पलते हैं, उन्हें सांस्कृतिक शिक्षा मिलती है। वे अपनी सारी अच्छाइयाँ-बुराइयाँ वहाँ से लेते हैं। हमारे । साहित्य तथा राजनीति के पास ऐसी कोई दृष्टि नहीं है जो परिवार को लागू हो....
प्रस्तुत पंक्तियाँ किस पाठ से लिया गया है ?01:27View Solutionसमाज में वर्ग हैं, श्रेणियाँ हैं। श्रेणियों में परिवार है। समाज की एक बुनियादी इकाई परिवार भी है। समाज की अच्छाई-बुराई । परिवार के माध्यम से व्यक्त होती है। मनुष्य के चरित्र का विकास. 1 परिवार में होता है। बच्चे पलते हैं, उन्हें सांस्कृतिक शिक्षा मिलती है। वे अपनी सारी अच्छाइयाँ-बुराइयाँ वहाँ से लेते हैं। हमारे । साहित्य तथा राजनीति के पास ऐसी कोई दृष्टि नहीं है जो परिवार को लागू हो....
समाज की एक बुनियादी इकाई है00:52View Solutionसमाज में वर्ग हैं, श्रेणियाँ हैं। श्रेणियों में परिवार है। समाज की एक बुनियादी इकाई परिवार भी है। समाज की अच्छाई-बुराई । परिवार के माध्यम से व्यक्त होती है। मनुष्य के चरित्र का विकास. 1 परिवार में होता है। बच्चे पलते हैं, उन्हें सांस्कृतिक शिक्षा मिलती है। वे अपनी सारी अच्छाइयाँ-बुराइयाँ वहाँ से लेते हैं। हमारे । साहित्य तथा राजनीति के पास ऐसी कोई दृष्टि नहीं है जो परिवार को लागू हो....
किसका विकास परिवार में होता है ?View Solution