सिद्ध कीजिए की किसी समलम्ब के विकर्णों के मध्य-बिन्दुओं को जोड़ने वाला रेखाखण्ड इसकी प्रत्येक भुजा के समान्तर तथा इन भुजाओं के अन्तर के आधे के बराबर होता है।
एक समलम्ब चतुभुर्ज ABCD जिसमे AB∣∣DC तथा विकर्णों AC तथा BD के मध्य-बिन्दु क्रमशः P तथा Q है।
सिद्ध करना है : (i) PQ∣∣AB अथवा DC
(ii)PQ=12(AB−DC)

रचना DP को मिलाइये तथा DP को इस प्रकार बढ़ाइए की AB को R पर मिले।
उपपत्ति : चूँकि AB∣∣DC तथा तिर्यक रेखा AC इन्हे क्रमशः A तथा C काटती है।
∴∠1=∠2 ...(i)[∴ एक एकान्तर कोण बराबर होते है]
अब त्रिभुजों APR तथा DPC में
∠1=∠2 [(i) से]
AP=CP [∴AC का मध्य-बिन्दु P है]
तथा ∠3=∠4 [ शीर्षभिमुख कोण]
अतः कोण-भुजा-कोण सर्वांगसम कसौटी से
ΔAPR≅ΔDPC
⇒AR=DC तथा PR=DP ...(ii) [ ∴ सर्वांगसम त्रिभुजों के संगत भाग बराबर होते है]
ΔDRB में DR तथा DB के मध्य-बिन्दु क्रमशः P तथा Q है।
∴PQ∣∣RB
⇒PQ∣∣AB [∴AB के एक भाग RB है]
⇒PQ∣∣AB तथा DC [∴AB∣∣DC(दिया है)]
यह (i) को सिद्ध करता है ।
पुनः ΔDRB भुजा में DR तथा DB के मध्य-बिन्दु क्रमशः P तथा Q है।
∴PQ=12RB⇒PQ=12(AB−AR)⇒PQ=12(AB−DC)[(ii) से , AR=DC]
यह समीकरण (ii) को सिद्ध करते है।
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.14videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.216videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन EXERCISE - बहु विकल्पीय प्रश्न22videos
घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन
- BOOK - RD SHARMACHAPTER - त्रिभुज तथा उसके कोण EXERCISE - बहु विकल्पीय प्रश्न28videos
त्रिभुज तथा उसके कोण
Similar Questions
एक चतुभुर्ज है तीन कोण क्रमशः 110∘,50∘ तथा 40∘ है। इसका चौथा कोण ज्ञात कीजिए।
07:05View Solutionएक समान्तर चतुर्भुज के दो सम्मुख कोण (3x−2)∘ तथा (50−x)∘ है। समान्तर चतुभुर्ज के प्रत्येक कोण की माप ज्ञात कीजिए?
06:09View Solutionयदि किसी घनाभ के तीन आसन्न फलकों के क्षेत्रफल A1,A2 व A3 से दर्शाया जावे तो इस घनाभ का आयतन होगा :
07:31View Solutionयदि किसी त्रिभुज के तीनो कोण बराबर हो, तो प्रत्येक कोण का माप होगा:
04:38View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
06:19View Solutionकिसी त्रिभुज के शीर्षो के निर्देशांक (2,5),(6−2) तथा (−3,−4) है , तो उसकी मध्यिकाओ के समीकरण ज्ञात कीजिए
03:15View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
03:17View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
06:19View Solutionयदि किसी त्रिभुज की भुजाओं के मध्य - बिंदुओं के निर्देशांक (2,1),(−1,−3) और (4,5) हों , तो उसके शीर्षों के निर्देशांक ज्ञात कीजिए ।
06:40View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
03:45View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
02:38View Solutionयदि किसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,0),(1,3) और (-1,2) हो तो उसके कोणों को ज्ञात कीजिए।
01:29:56View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
02:49View Solutionनिम्नलिखित संख्या युग्मों को कार्तीय तल के बिन्दुओं के रूप में आलेखित कीजिए :
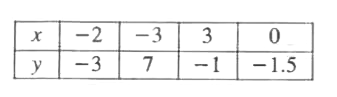 01:47View Solution
01:47View Solution−27 के साथ कितना जोड़ने पर जोड़ 45 के बराबर प्राप्त होगा ?
View Solutionदो रेखाओ के मध्य के कोणों के अर्द्धकों के समीकरण
View Solution

