Complete the activity by filling the boxes.
In the given figure , ∠BAC=80∘ ,∠ABC=30∘ and m (arc BQC)=160∘.
Find (i) m(arc APC) (ii) m (arc AB).
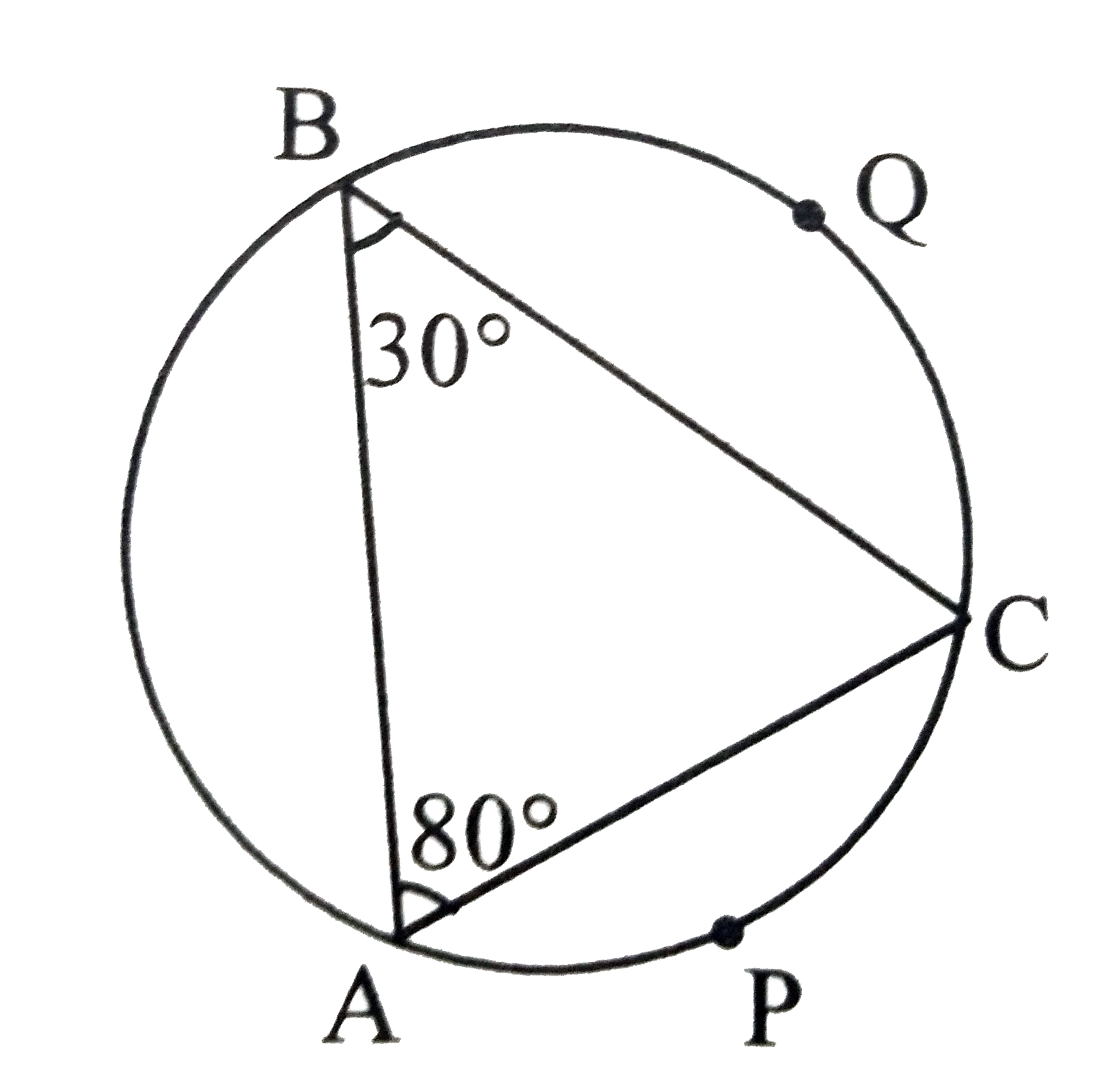
The correct Answer is:(i) ∴ m (arc APC)=60∘ (ii) ∴ m(arc AB)=140∘
Step by step video & image solution for Complete the activity by filling the boxes. In the given figure , angleBAC=80^@ ,angleABC=30^@ and m (arc BQC)=160^@. Find (i) m(arc APC) (ii) m (arc AB). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Multiple Choice Question
25 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Additional Problems for Practice
32 Videos
- CIRCLEBOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Problem Set-3
25 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics
4 Videos
- CO-ORDINATE GEOMETRYBOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT
19 Videos
Similar Questions
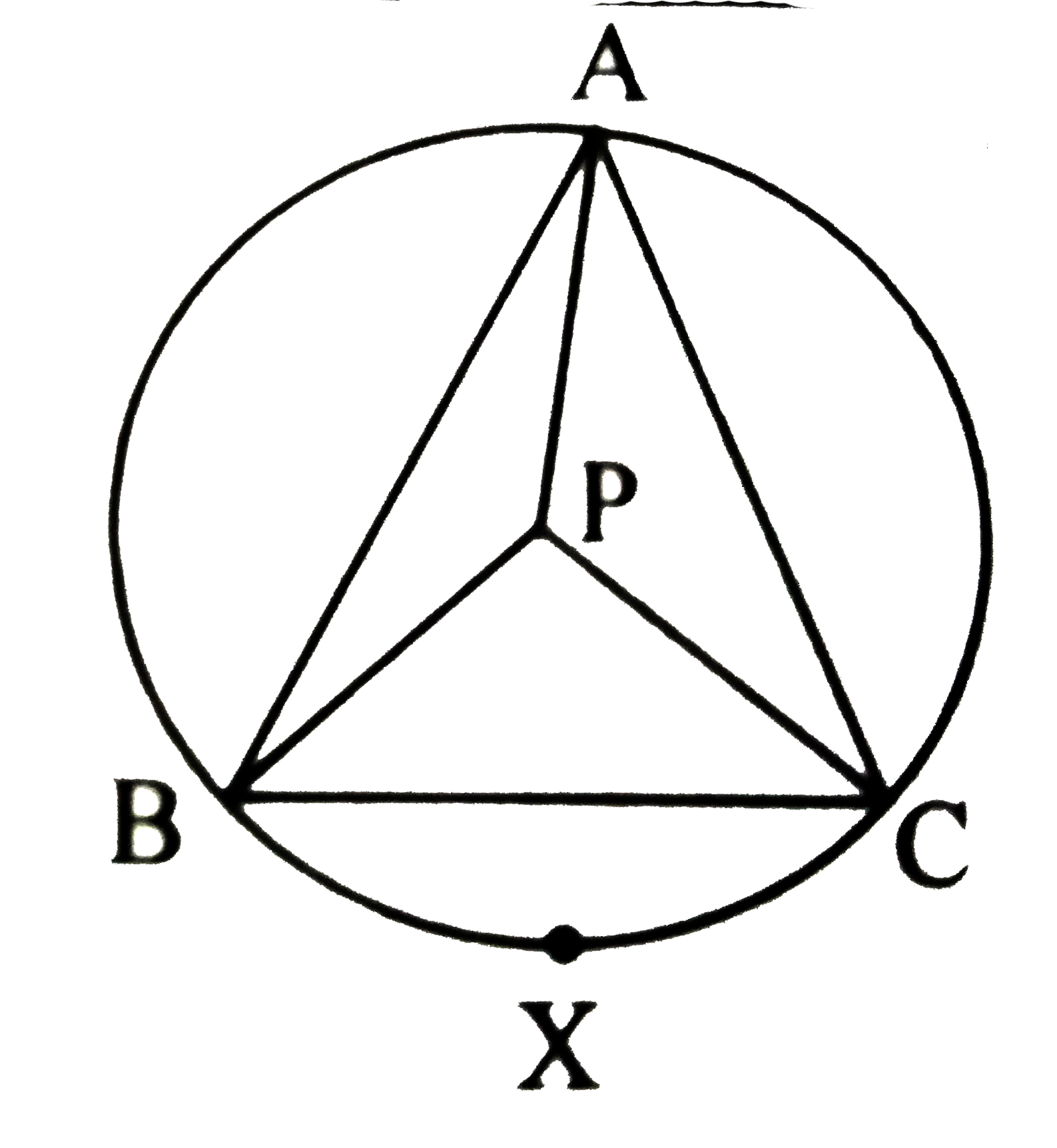
In the adjoining figure, P is the circumcentre of the ΔABC.m∠APC=118∘ and m∠PBC=45∘ , then find:
(i) m(arc BXC)
(ii) m(arc BCA)
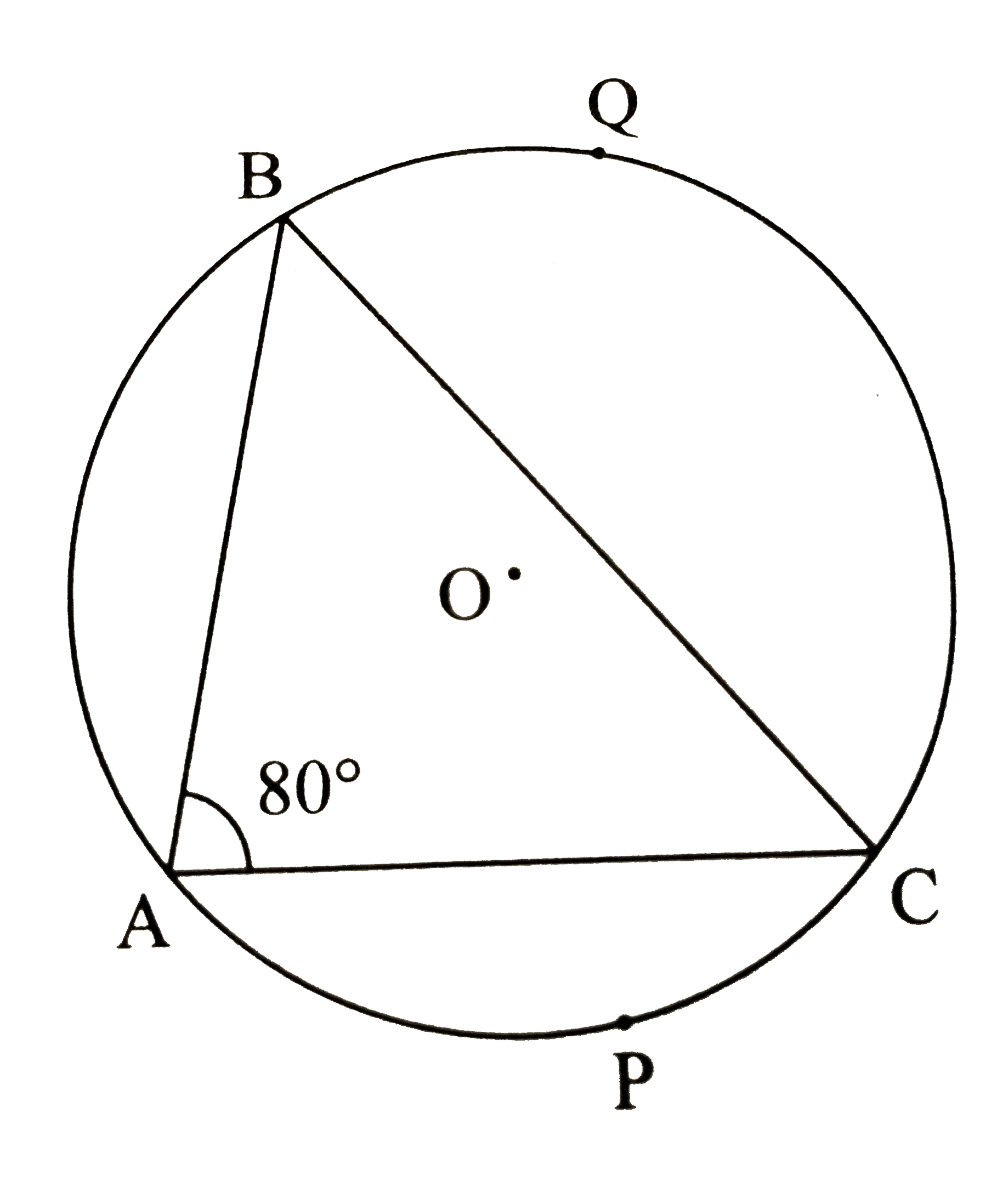
View SolutionIn the figure, O is the centre of the circle , ∠BAC=80∘, m ( arc APC ) =60∘ then find the measure of
(i) ∠ABC (ii) arc BQC
View SolutionIn the figure, seg AB is the diameter of the circle, ∠ABC=30∘, Find (1) m(arc AXC)
(2) m(arc BYC)

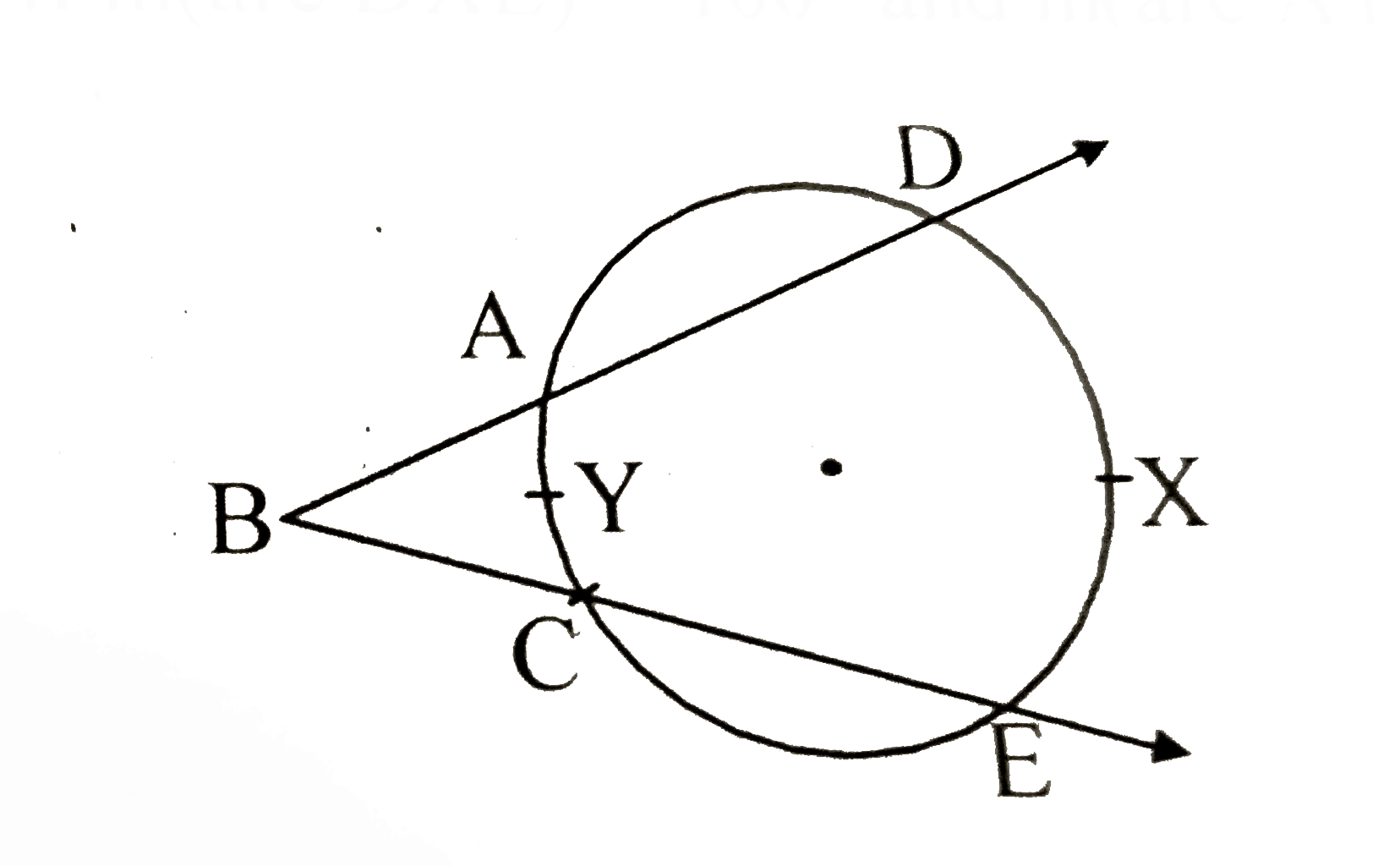
View SolutionIn the figure , if m ( arc DXE 0 =100∘ and m (arc AYC ) =40∘, find ∠DBE.

View SolutionIn the following figure, if m(arc DXE) =100∘ and m(arc AYC) =40∘, find ∠DBE.
View SolutionIn the adjoninog figure , radius of the circle is 7 cm and m (arc MBN) = 60∘ find
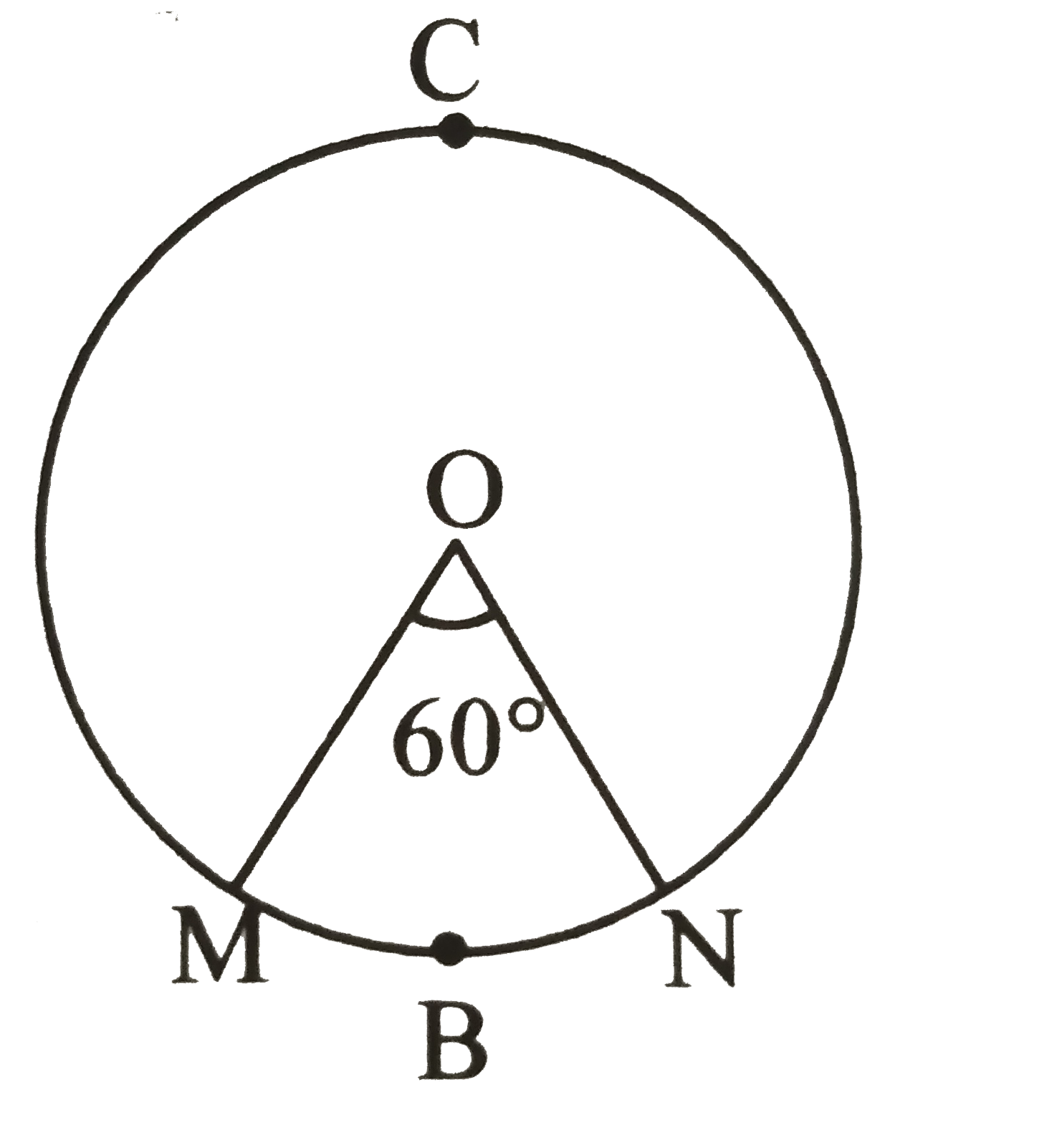
A(O-MCN).
View SolutionIn the adjoninog figure , radius of the circle is 7 cm and m (arc MBN) = 60∘ find

A ( O-MBN).
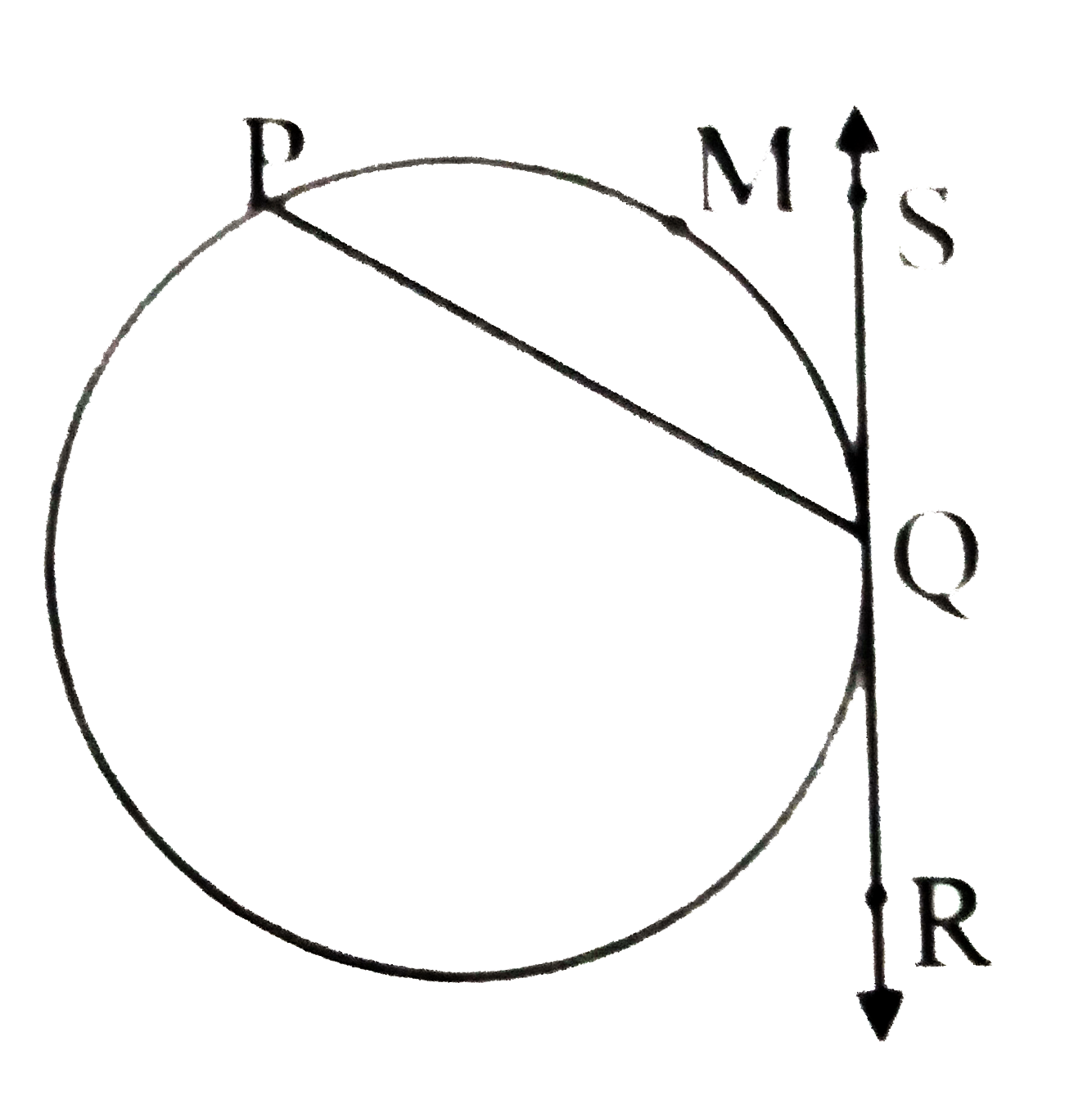
View SolutionIn the following figure , m(arc PMQ)=110∘, then ∠PQS=
View SolutionIn the given figure , O is the centre of the circle. If m(arc AXB)=80∘, then m∠AOB=

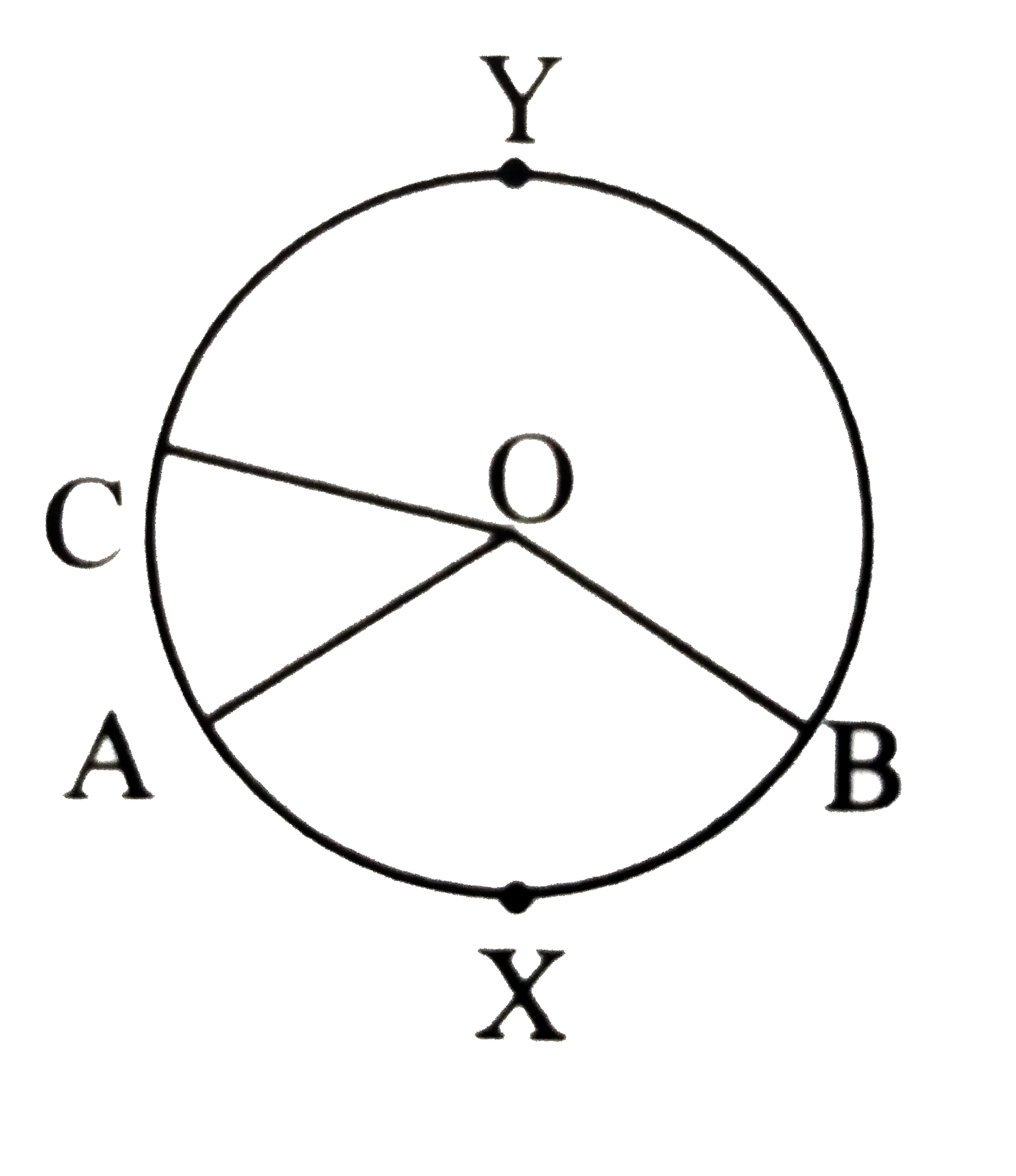
View SolutionIn the given figure, O is the centre of the circle .
∠AOB=120∘,m(arc AC)=55∘.
Use the given information and fill the boxes.
(i)m(arcAXB)=□ (ii) m(arcCAB)=□ (iii) ∠COB=□ (iv) m(arcAYB)=□
View Solution
