The image obtained while finding the focal length of a convex lens is ……………… .
real and erect.
virtual and erect.
realandinverted
virtual and inverted
The correct Answer is:C
Step by step video, text & image solution for The image obtained while finding the focal length of a convex lens is ……………… . by Physics experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - LENSES EXERCISE - Complete the paragraph1videos
LENSES
- BOOK - TARGET PUBLICATIONCHAPTER - LENSES EXERCISE - Name the following11videos
LENSES
- BOOK - TARGET PUBLICATIONCHAPTER - LENSES EXERCISE - Solve the following problems9videos
LENSES
- BOOK - TARGET PUBLICATIONCHAPTER - HEATEXERCISE - Values to remember10videos
HEAT
- BOOK - TARGET PUBLICATIONCHAPTER - MODEL QUESTION PAPER (PART -1 )EXERCISE - Questions21videos
MODEL QUESTION PAPER (PART -1 )
Similar Questions
Knowledge Check
- Question 1 - Select One
The image obtained while finding the focal length of convex lens is_____
AA real and crectBVirtual and erect .CReal and invertedDVirtual and inverted - Question 2 - Select One
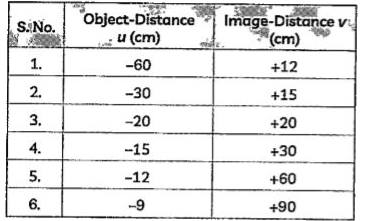
The focal length of the convex lens isA+10 cmB+20cmC−10cmD−20cm - Question 3 - Select One
Focal length of a convex lens is maximum for
Ablue lightByellow lightCgreen lightDred light
A convex lens is placed between an object and a screen which are at a fixed distance apart for one position of the lens. The magnification of the image obtained on the screen is m1. When the lens is moved by a distance d the magnification of the image obtained on the same screen m2, Find the focal length of the lens.
View SolutionFocal length of convex lens will miximum for
View SolutionFocal length of a convex lens will be maximum for
View SolutionFocal length of a convex lens will be maximum for
View SolutionAn object is placed 30cm away from a convex lens of focal length 10cm and a sharp image is formed on a screen. Now, a convex lens is placed In contact with the convex lens. The screen now has to be moved by 45cm to get a sharp image again. The magnitude of focal length of the convex lends in (in cm)
View Solution

