A satellite is revolving in an orbit a height 20200 km from the suface of the earth . Determine the speed with which the satellite is revolving around the earth. Also calcutate the time taken by the satellite to compete on revolution around the earth.

Video Solution

Text Solution

Verified by Experts

Analyse
Step 1: Analyse the given data in the problem and find out what needs to be calculated.
Given : Height from the surface of the earth =20200 km = $2.02 \times 10^{7} m$
Also we know values of the basic physical constants like G,M and R :

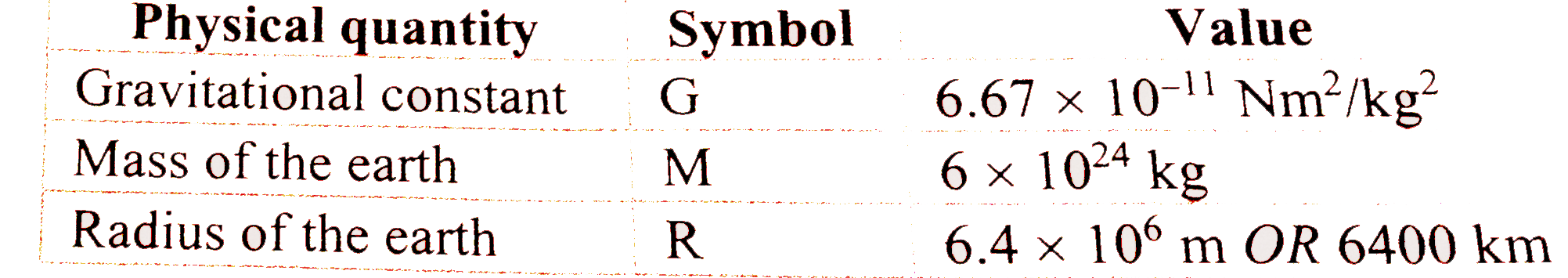
To find . (i) Tangential velocity $(v_{c})$
(ii) Time period of satellite (T)
Solve
Step 2: Write the formula foe tangential velocity,
$v_{c} = \sqrt{\frac{G M}{r}} (i)$
Before getting started with tedious calcutions , first calculate the radius of the orbit from the centre of the earth.
R is the radius of the earth . As shown in figure ,the radius of the orbit 'r' is (R+H).
$∴ r = R + H = 6400 + 20200 = 26600 km = 2.66 \times 10^{7} m$
Step 3 : Using equation (i) and substituing know values,
$v_{c} = \sqrt{\frac{6.67 \times 10^{- 11} \times 6 \times 10^{24}}{2.66 \times 10^{7}}}$
Step 4 : Separate the powers of 10 for simplification .
$∴ v_{c} = \sqrt{\frac{6.67 \times 6}{2.66} \times 10^{6}}$
For further simplification of calculation , take approximate values and contiue calcution.
$v_{c} \approx \sqrt{\frac{7 \times 6}{3} \times 10^{6}} = \sqrt{7 \times 2} \times 10^{3} = \sqrt{4} \times 10^{3}$
Step 5 : As, 14 is not a perfect square we again use approximation for arriving at the final answer. ltbrlt Find out the upper and lower perfect squares near the required number.
Here, these values would be 9 and 16 . Hence our answer lies somewhere between 3 and 4 Also , 14 is much closer to 16 as compared to 9 which leads us to conclude the approximate value of $\sqrt{14} \approx 3.8 .$
$∴ v_{c} = 3.8 \times 10^{3} m/s or 3.8 km/s$
Step 6 : To complete one revolution around the earth , the satellite travels distance equal to circumference of the orbit.
$∴ Here,velocity (v_{c}) = \frac{distance}{time} = \frac{2 π r}{T} \Rightarrow T = \frac{2 π r}{v_{c}}$
$∴ T = \frac{2 \times 3.14 \times 2.66 \times 10^{7}}{3.8 \times 10^{3}}$
Using approximations, .
$T \approx = \frac{2 \times 3 \times 3}{4} \times 10^{4} = 4.5 \times 10^{4} s$
To convert the time in hours , divide the answer with 3600,
$T = \frac{45000}{3600} = \frac{25}{2} = 12.5 hours$
Answer check
without approximation , the answers to velocity of satellite and its time period will be as follows,
$v_{c} = \sqrt{\frac{6.67 \times 10^{- 11} \times 610^{24}}{2.66 \times 10^{7}}} = 3878.8 m/s or 3.88 km/s$
$T = \frac{2 \times 3.14 \times 2.66 \times 10^{7}}{3.88 \times 10^{3}} = 43053 s = 11.96 hours$

Updated on:21/07/2023

For a satellite revolving around the earth
Aits P.E. and K.E. are +ve and the total energy is negative
Bits P.E. and K.E. are -ve but the total energy is positive
Cits P.E. and total energy are negative but the K.E. is positive
Dits P.E. and total energy are positive but its K.E. is negative
A satellite revolving around the earth is
Aan inertial frame
Ba non-inertial frame
Cboth an inertial and non-inertial frame
Dinertial only when the height of the satellite is high
A satellite is revolving round the earth in an elliptical orbit :
AGravitational force exerted by earth to centripetal force at every point of trajectory.
BPower associted with gravitational force is zero at every point
CWork done by gravitational force is zero in some shell parts of the orbit
DAt some point, magnitude of gravitational force is greater than that of centripetal force