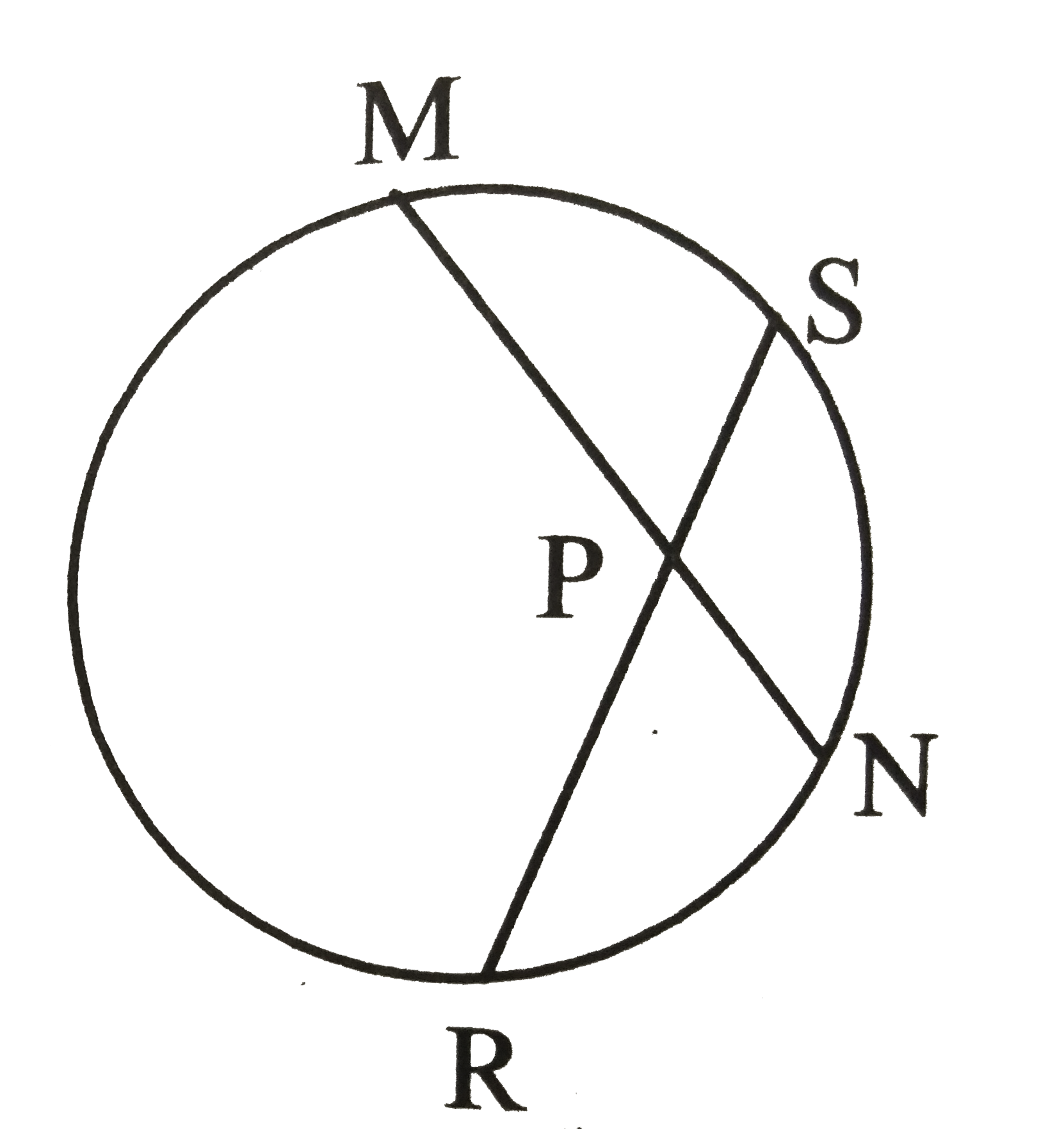
In the figure, chord MN and chord RS intersect at point D.
(1) If RD = 15, DS = 4, MD = 8 , find DN.
92) If RS = 18, MD = 9 , DN = 8 , find DS .

The correct Answer is:12 or 6
Let DS=x
DR+DS=RS (R−D−S)
∴DR+x=18
∴DR=(18−x)
Chords MN and RS intersect each other at point D inside the circle.
∴ by theorem of internal division of chords,
DM×DN=DR×DS
∴9×8=(18−x)×x
∴72=18x−x2
x2−18x+72=0
∴x2−12x−6x+72=0
∴x(x−12)−6(x−12)=0
∴(x−12)(x−6)=0
Either x-12=0 or x-6=0
∴x=12 or x=6
∴DS=12 or DS=6.
Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PROBLEM SET 3
50 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - Challenging Questions
10 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PRACTICE SET 3.4
15 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
Knowledge Check
Two chords AB and PQ of a circle mutually intersect at an outside point D. If AD=12 cm, AB=8 cm, DQ=6 cm then find PQandPD.
AA)2&6BB)2&8CC)3&6DD)5&7
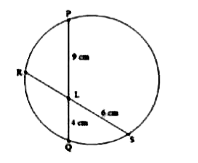
In the given figure, chords PQ and RS intersect each other at point L Find the length of RL.
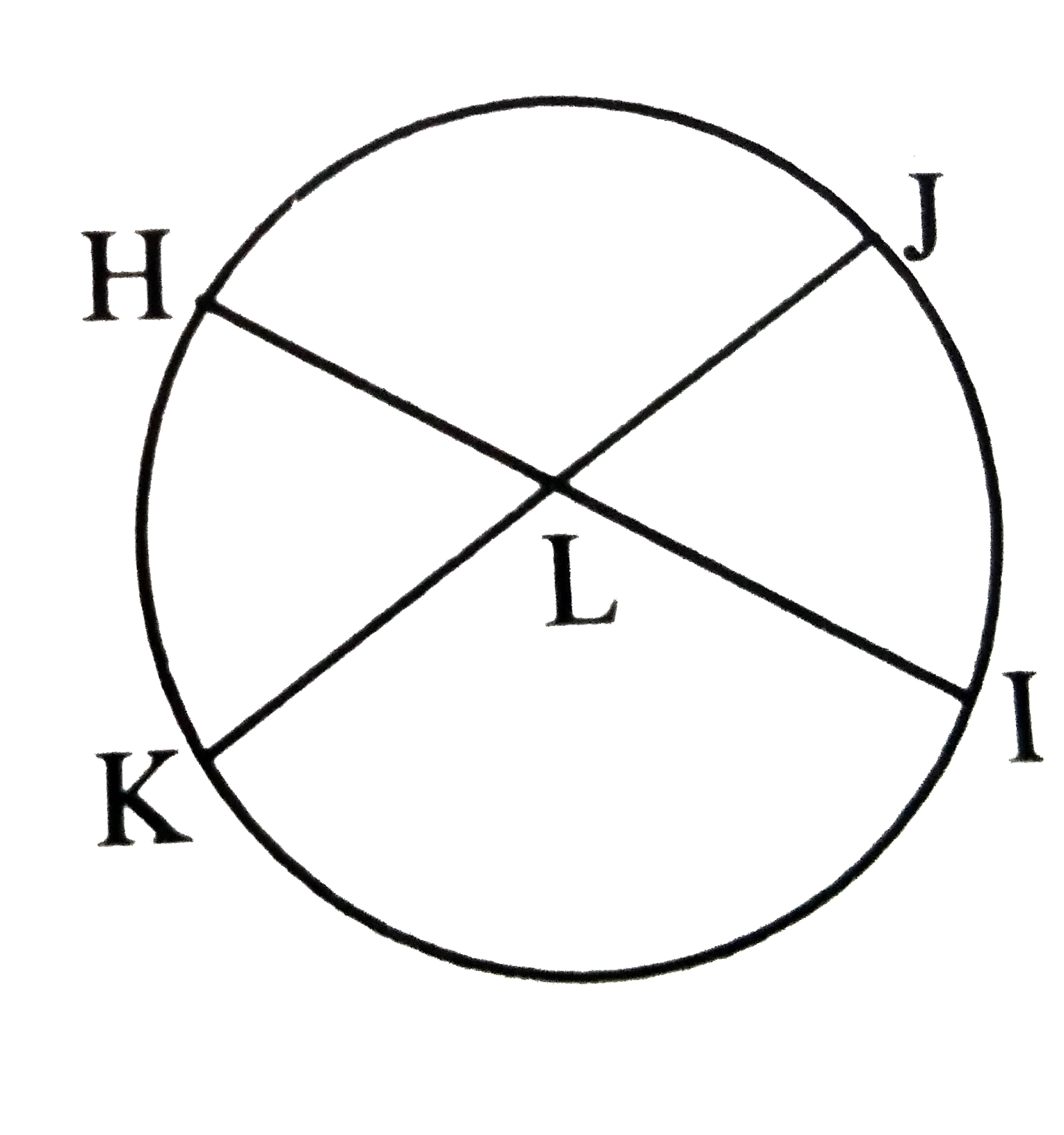
View SolutionIn the adjoining figure , chords HI and KJ intersect at point L. If KL=8,LJ=5 and HI=14, then find the length of HL.
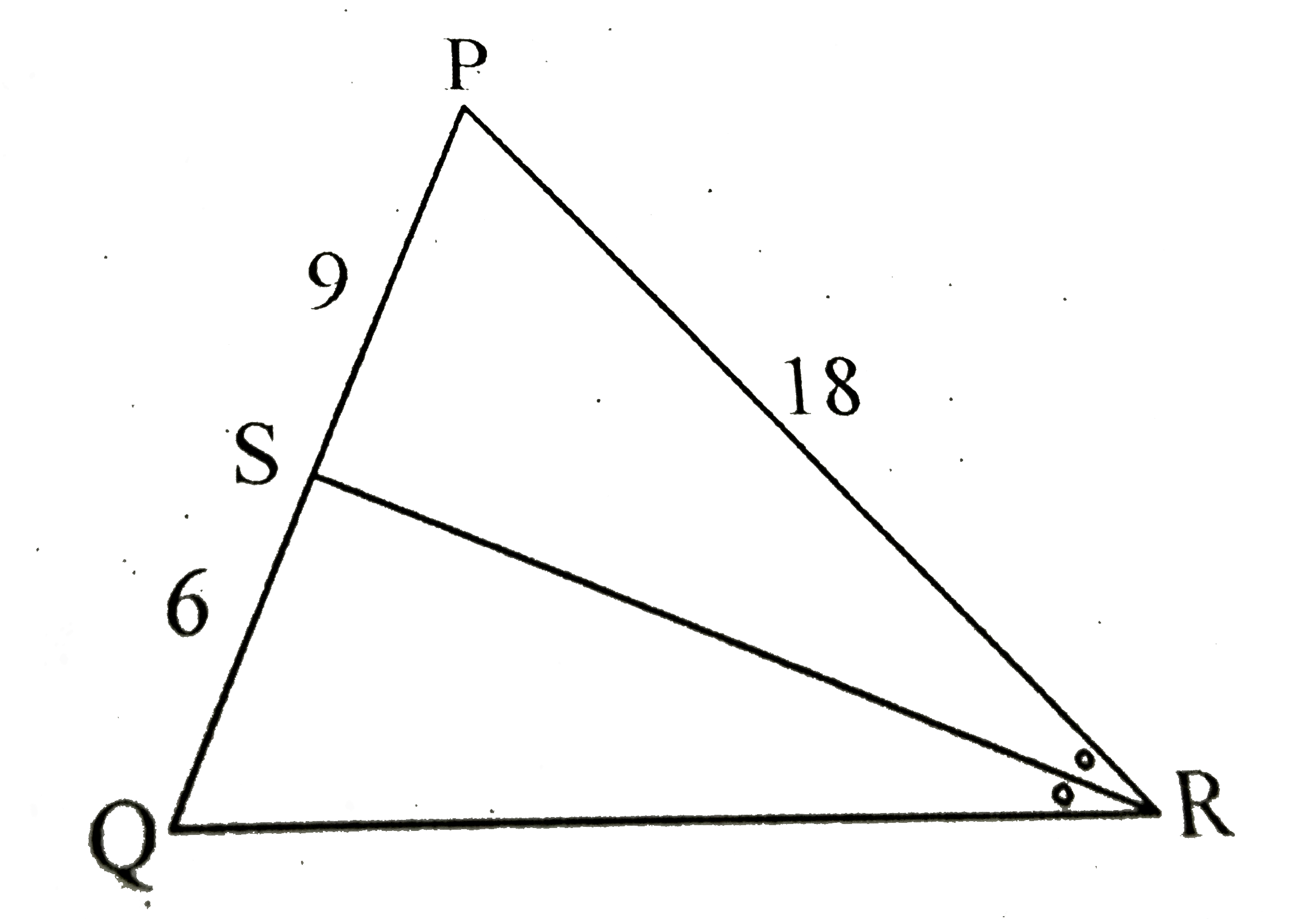
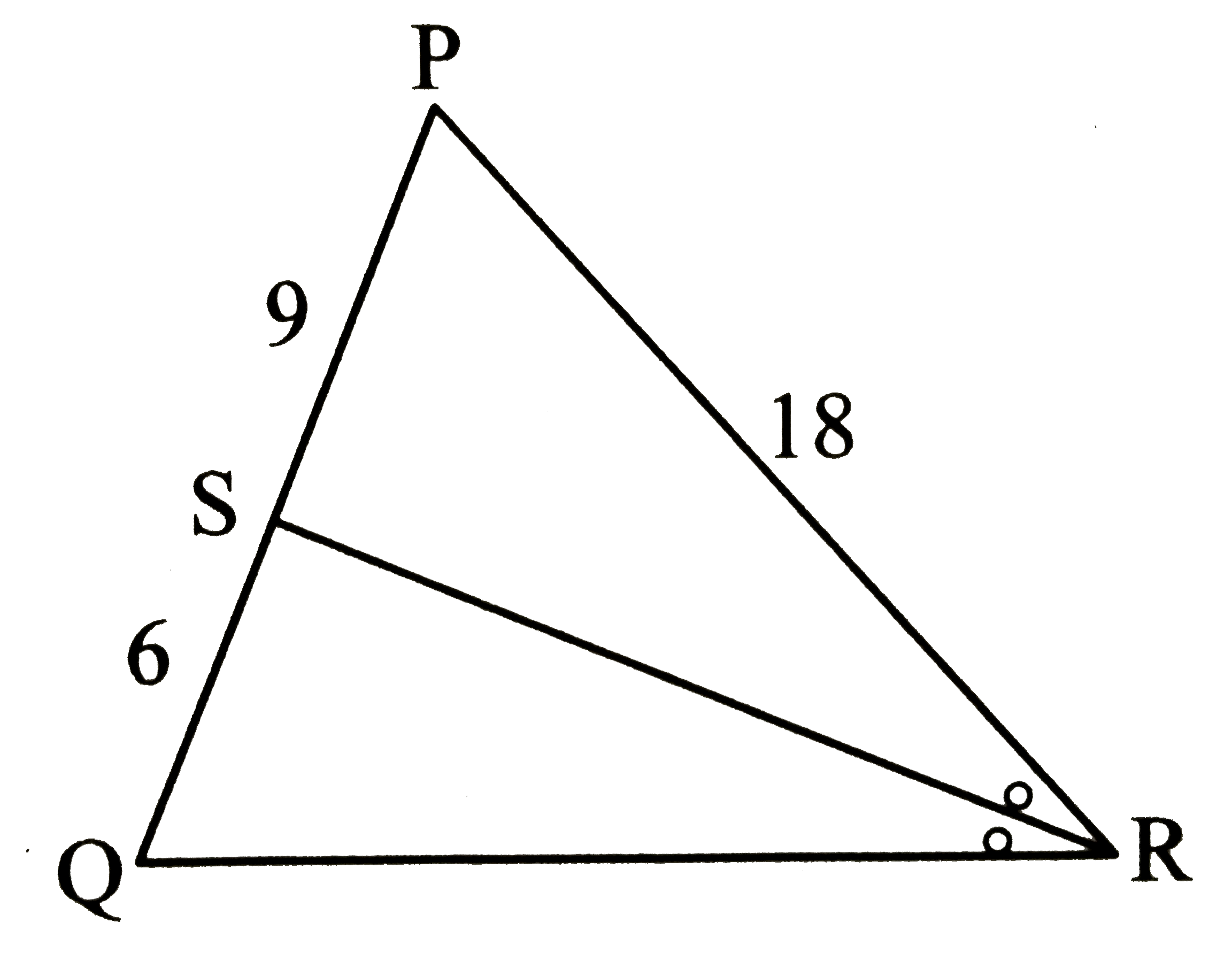
View SolutionIn the following figure, in ΔPRQ, seg RS is the bisector of ∠PRQ. If PS=9,SQ=6,PR=18, find QR.
View SolutionIn the figure, diameter AB and chord CD intersect in point E.
If m (arc CXB ) = 100∘. Find
(i) ∠ADC
(ii)∠CDB
(iii) ∠ACB

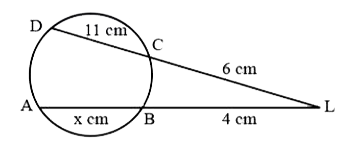
View SolutionIn the given figure, chords AB and CD are intersecting each other at point L. Find the length of AB.
View SolutionIn the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 9, SQ = 6, PR = 18, find QR.
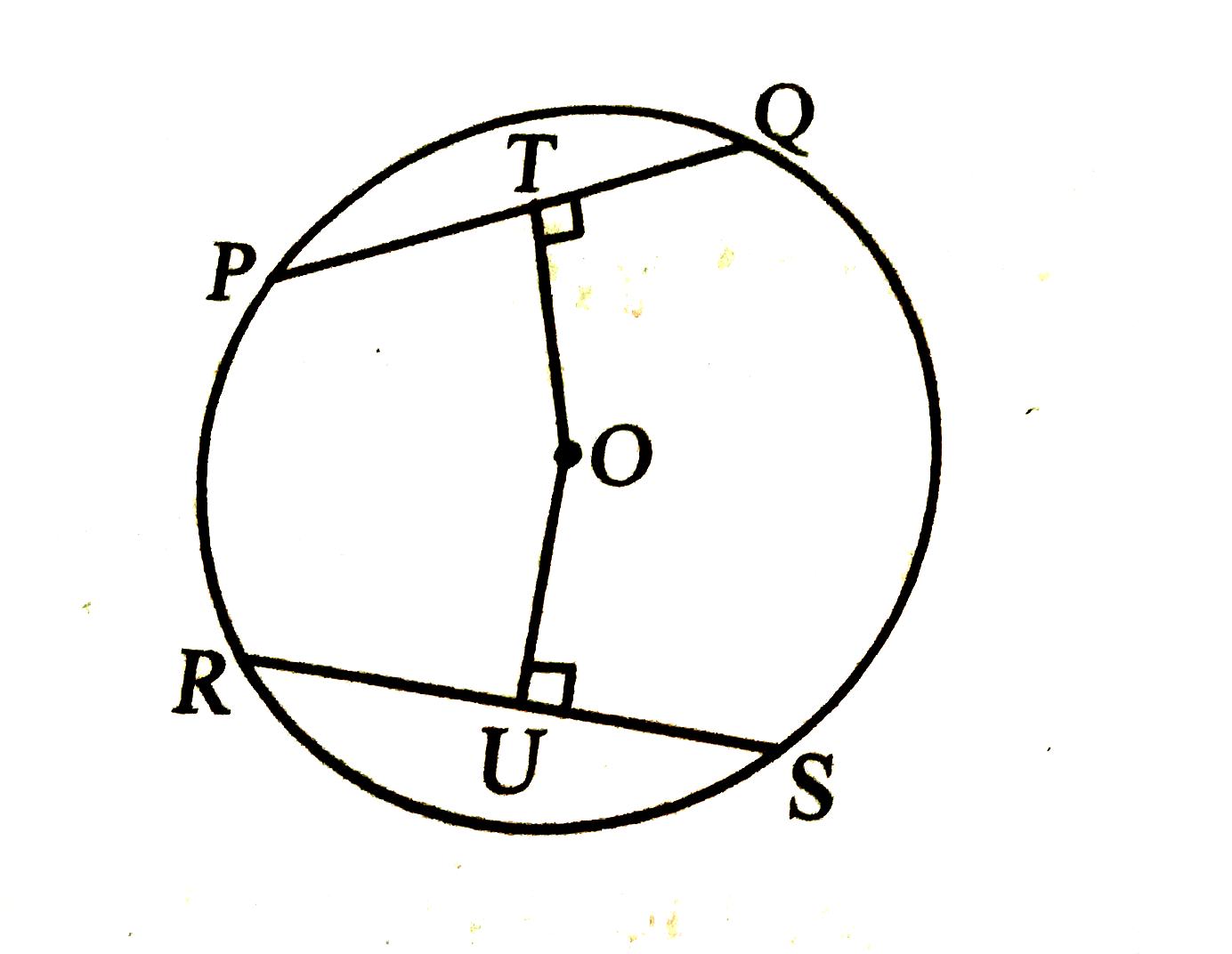
View SolutionIn the given figure, O is the center and chord PQ = Chord RS. If OT = 5 cm, then find OU.
View Solution