Find the co-ordinates of the points of trisection of the line segment AB with $A (2, 7) and B (- 4, - 8)$

Video Solution

Text Solution

Verified by Experts

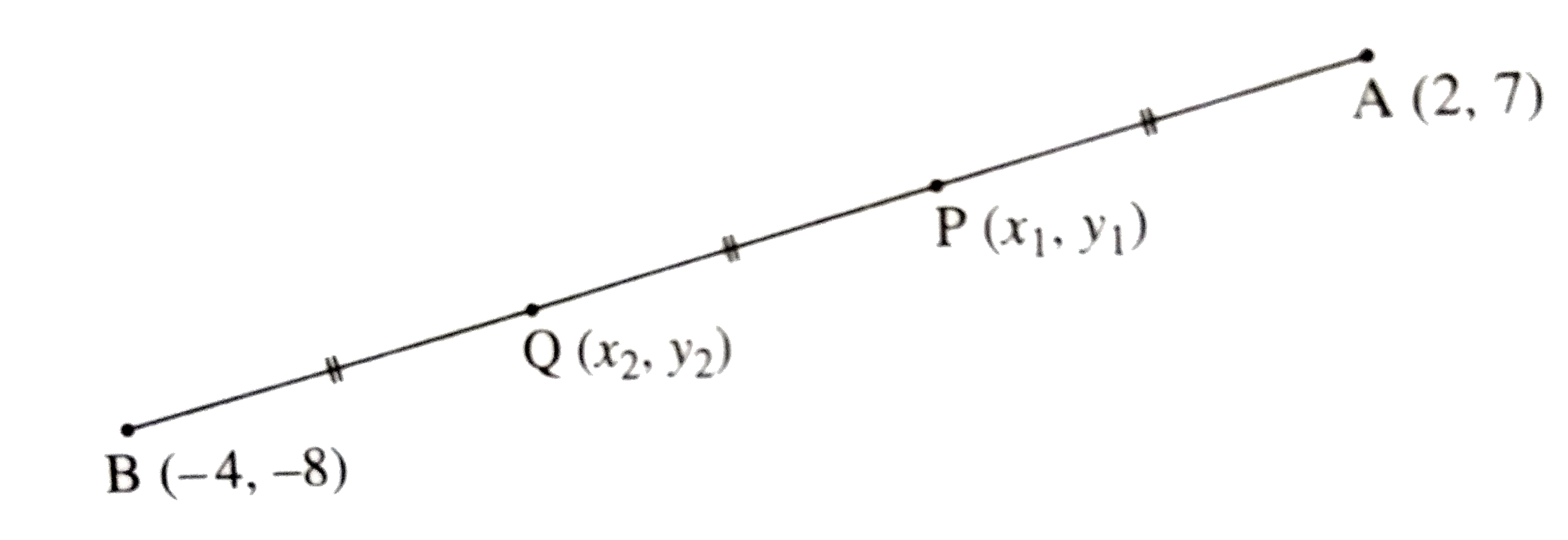
$A (2, 7)$ and $B (- 4, - 8)$
Let $P (x_{1}, y_{1})$ and $Q (x_{2}, y_{2})$ be the points of trisection.
$∴ A P = P Q = Q B$ ….1
$\frac{A P}{P B} = \frac{A P}{P Q + Q B}$ ……… $(P - Q - B)$
$∴ \frac{A P}{P B} = \frac{A P}{A P + A P}$ …..[From 1]
$∴ \frac{A P}{P B} = \frac{A P}{2 A P} ∴ \frac{A P}{P B} = \frac{1}{2}$
$∴ A P : P B = 1 : 2$
$∴ P$ divides segment AB in the ratio $1 : 2$ .
By section formula,
$x_{1} = \frac{1 (- 4) + 2 (2)}{1 + 2}, y_{1} = \frac{1 (- 8) + 2 (7)}{1 + 2}$
$∴ x_{1} = \frac{- 4 + 4}{3}, ∴ y_{1} = \frac{- 8 + 14}{3}$
$∴ x_{1} = \frac{0}{3}, ∴ y_{1} = \frac{6}{3}$
$∴ x_{1} = 0, ∴ y_{1} = 2$
$∴$ the coordinates of point P are (0,2).
$\frac{A Q}{Q B} = \frac{A P + P Q}{Q B} = ... ... ... (A - P - Q)$
$∴ \frac{A Q}{Q B} = \frac{Q B + Q B}{Q B}$ .......[From 1]
$∴ \frac{A Q}{Q B} = \frac{2 Q B}{Q B}$
$∴ \frac{A Q}{Q B} = \frac{2}{1}$
$∴ Q$ divides segment AB in the ratio $2 : 1$ .
By section formula,
$x_{2} = \frac{2 (- 4) + 1 (2)}{2 + 1}, y_{2} = \frac{2 (- 8) + 1 (7)}{2 + 1}$
$∴ x_{2} = \frac{- 8 + 2}{3}, ∴ y_{2} = \frac{- 16 + 7}{3}$
$∴ x_{2} = \frac{- 6}{3}, ∴ y_{2} = \frac{- 9}{3}$
$∴ x_{2} = - 2, ∴ y_{2} = - 3$
$∴$ the coordinates of point Q are $(- 2, - 3)$ .
The coordinates of the points of trisection of the line segment AB are (0,2) and $(- 2, - 3)$ .

Updated on:21/07/2023

|

Class 10 MATHS COORDINATE GEOMETRY

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile