Question

Find the coordinates of centre of the circle passing through the
points P(6,-6),Q (3,-7) and R(3,3)

Explanation

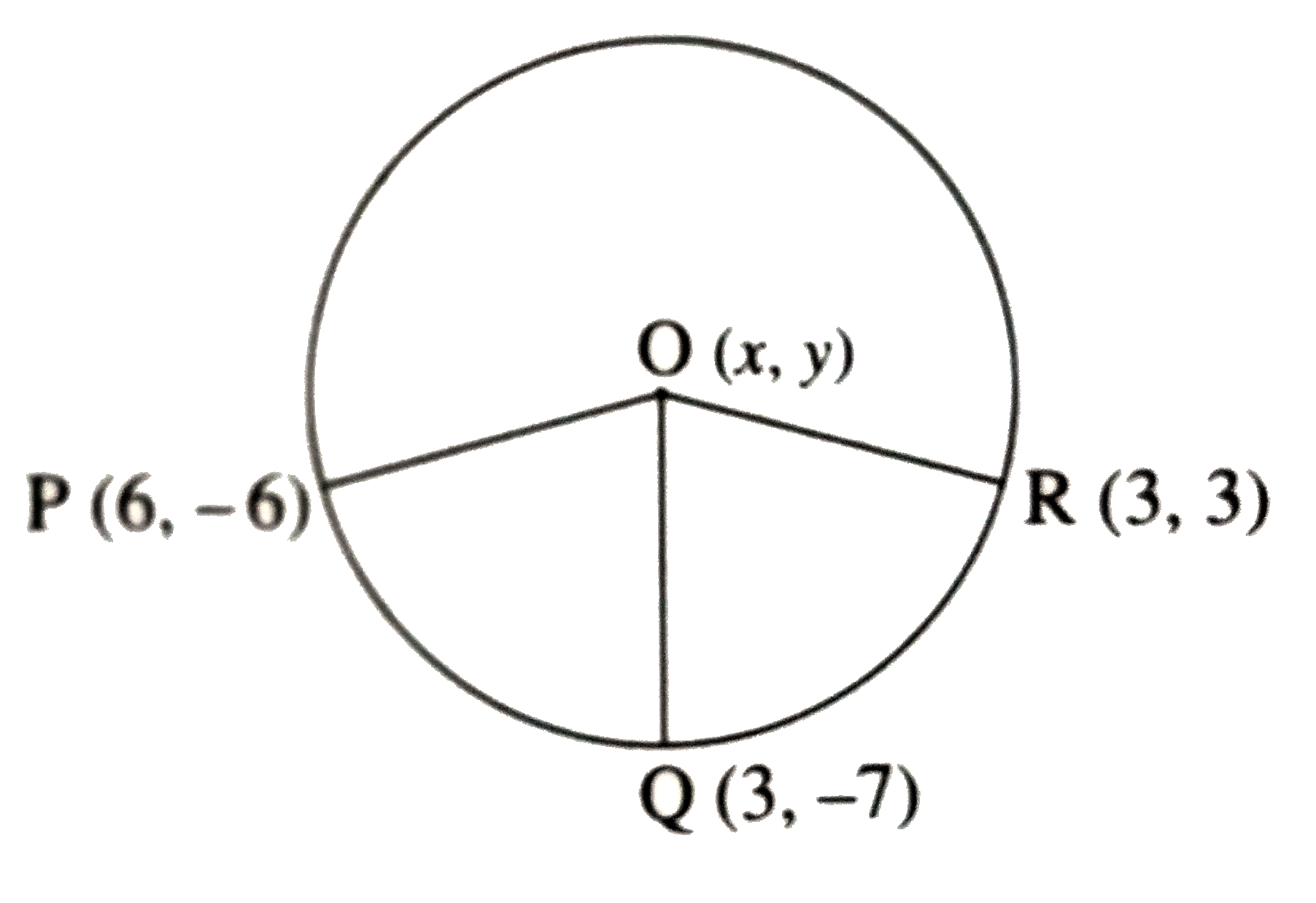
`P(6,-6),Q(3,-7)` and `R(3,3)`
Let `O(x,y)` be the centre of the circle passing through the points P,Q and R.
`OP=OQ` ……(Radii of the same circle)
`sqrt((x-6)^(2)+[y-(-6)]^(2))=sqrt((x-3)^(2)+[y-(-7)]^(2))`
Squaring both the sides, we get
`(x-6)^(2)+(y+6)^(2)=(x-3)^(2)+(y+7)^(2)`
`:.x^(2)-12x+36+y^(2)+12y+36`
`=x^(2)-6x+9+y^(2)+14y+49`
`:.-12x+12y+72=-6x+14y+58`
`:.-12x+6x+12y-14y=58-72`
`:.-6x-2y=-14`
`:.-2(3x+y)=-14`
`:3x+y=(-14)/(-2)`
`:.3x+y=7` ......1
`OQ=OR`.........(Radii of the same circle)
`sqrt((x-3)^(2)+[y-(-7)]^(2))=sqrt((x-3)^(2)+(y-3)^(2))`
Squaring botht he sides, we get
`(x-3)^(2)+(y+7)^(2)=(x-3)^(2)+(y-3)^(2)`
`:.(y+7)^(2)=(y-3)^(2)`
`:.y^(2)+14y+49=y^(2)-6y+9`
`:.14y+6y=9-49`
`:.20y=-40`
`:.y=(-40)/20`
`:.y=-2`
Substituting `y-2` in 1 we get
`3x+(-2)=7`
`:.3x-2=7`
`:.3x=7+2, :.3x=9`
`:.x=9/3, :.x=3`
Coordinates of the centre of the circle are `(3,-2)`.