Find the possible pairs of co-ordinates of the fourth vertex D of the parallelogram, if three of its vertices are $A (5, 6), B (1, 2) and C (3, - 2)$

Video Solution

Text Solution

Verified by Experts

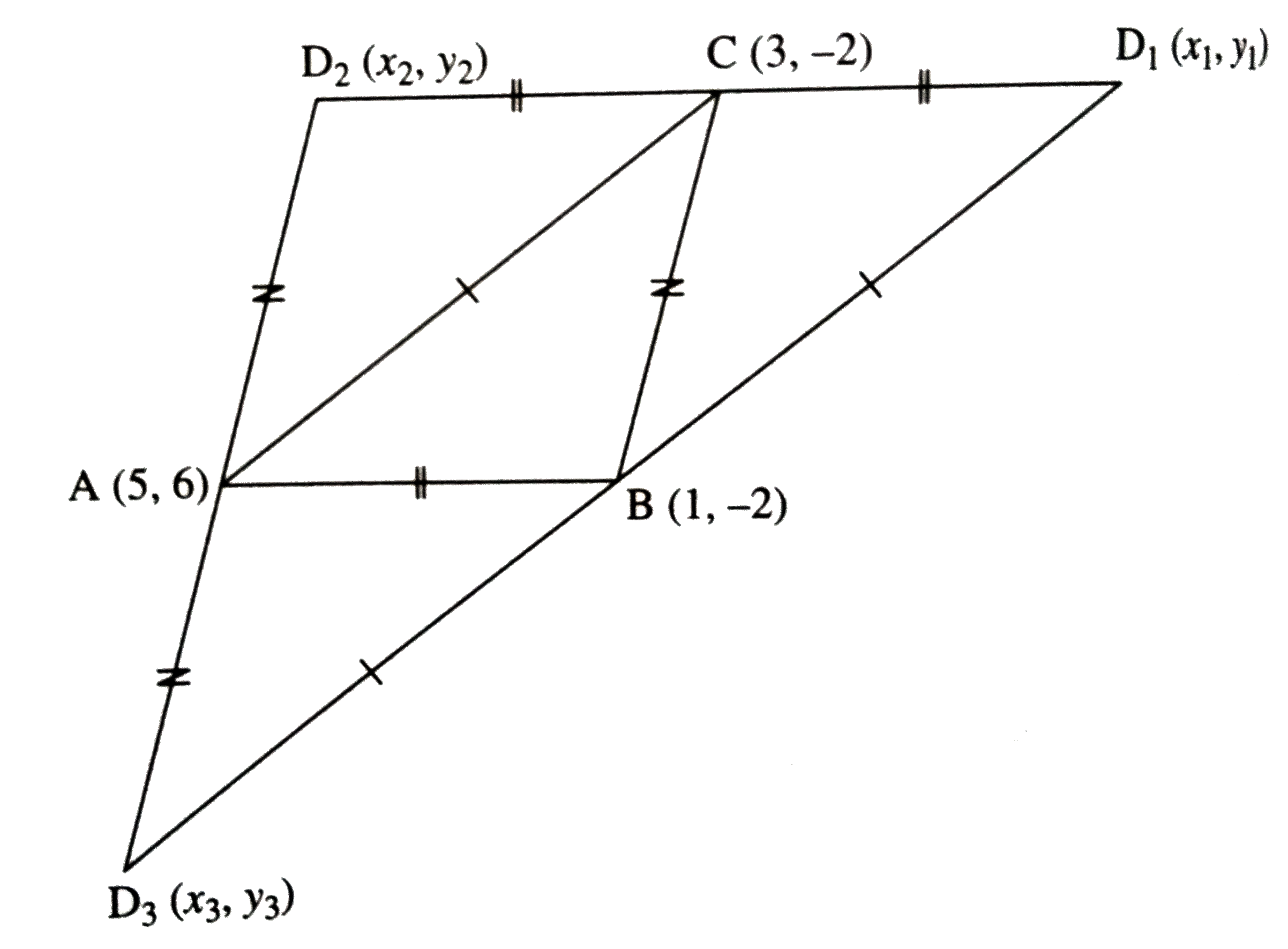
$A (5, 6), B (1, - 2)$ and $C (3, - 2)$ are the vertices of a parallelogram.
There can be three possibilities of the location of the vertex D, say $D_{1} (x_{1}, y_{2}), D_{2} (x_{2}, y_{2})$ and $D_{3} (x_{3}, y_{3})$ as shown in the figure.
$□ A B D_{1} C$ is a parallelogram.
$∴ A B = C D_{1}$
......(Opposite sides of parallelogram are equal ) .........1
also $□ A B C D_{2}$ is parallelogram.
$∴ A B = C D_{2}$
.........(Opposite sides of parallelogram are equal) ..........2
$∴$ From 1 and 2
$C D_{1} = C D_{2}$
$∴ C$ is the midpoint of $D_{2} D_{1}$ .
Similarly B is the midpoint of $D_{1} D_{3}$
and A is the midpoint of $D_{2} D_{3}$
Now C is the midpoint of $D_{2} D_{1}$
$∴$ by midpoint formula
$3 = \frac{x_{2} + x_{1}}{2}$
$∴ x_{1} + x_{2} = 6$ .............3
Similarly $x_{2} + x_{3} = 10$ .......4
and $x_{1} + x_{3} = 2$ .........5
Adding 3, 4 and 5 we get
$x_{1} + x_{2} + x_{2} + x_{3} + x_{1} + x_{3} = 6 + 10 + 2$
$∴ 2 x_{1} + 2 x_{2} + 2 x_{3} = 18$
$∴ 2 (x_{1} + x_{2} + x_{3}) = 18$
$∴ x_{1} + x_{2} + x_{3} = \frac{18}{2}$
$∴ x_{1} + x_{2} + x_{3} = 9$ .....6
Substituting 3 in 6 we get
$6 + x_{3} = 9$
$∴ x_{3} = 9 - 6$
$∴ x_{3} = 3$
Substituting 4 in 6 we get
$x_{1} + 10 = 9$
$∴ x_{1} = 9 - 10$
$∴ x_{1} = - 1$
Substituting 5 in 6 we get
$x_{2} + 2 = 9$
$∴ x_{2} = 9 - 2$
$∴ x_{2} = 7$
$∴ x_{2} = 7$
C is the midpoint of $D_{2} D_{1}$ .
$∴$ by midpoint formula,
$- 2 = \frac{y_{1} + y_{2}}{2}$
$∴ y_{1} + y_{2} = - 4$ ..7
Similarly $y_{2} + y_{3} = 12$ ............8
and $y_{1} + y_{3} = - 4$ .....9
Adding 7, 8 and 9 we get
$y_{1} + y_{2} + y_{2} + y_{3} + y_{1} + y_{3} = - 4 + 12 - 4$
$∴ 2 y_{1} + 2 y_{2} + 2 y_{3} = 4$
$∴ 2 (y_{1} + y_{2} + y_{3}) = 4$
$∴ y_{1} + y_{2} + y_{3} = \frac{4}{2}$
$∴ y_{1} + y_{2} + y_{3} = 2$ .....10
Substituting 7 in 10 we get
$- 4 + y_{3} = 2$
$∴ y_{3} = 2 + 4$
$∴ y_{3} = 6$
Substiting 8 in 10 we get
$y_{1} + 12 = 2$
$∴ y_{1} = 2 - 12$
$∴ y_{1} = - 10$
Substituting 9 and 10 we get
$y_{2} + (- 4) = 2$
$∴ y_{2} - 4 = 2$
$∴ y_{2} = 2 + 4$
$∴ y_{2} = 6$
The coordinates of point $D_{1}$ are $(- 1, 10)$
The coordinates of point $D_{2}$ are (7,6).
The coordinates of point $D_{3}$ are (3,6).
The possible pairs of coordinates of the fourth vertex D of the parallelogram are $(- 1, - 10), (7, 6)$ and $(3, 6)$ .

Updated on:21/07/2023

The fourth vertex D of a parallelogram $A B C D$ whose three vertices are $A (- 2, 3)$ , $B (6, 7)$ and $C (8, 3)$ is
A $(0, 1)$
B $(0, - 1)$
C $(- 1, 0)$
D $(1, 0)$
What is the fourth vertex of a parallelogram, if its three consecutive vertices are (-2,-1), (1,0) and (4,3)?
A $(0, - 2)$
B $(2, 2)$
C $(2, 1)$
D $(1, 2)$
Find the fourth vertex of the parallelogram whose three consecutive vertices are $(8, 8), (6, 1)$ and $(- 1, 1)$ .
A $(1, 8)$
B $(2, 9)$
C $(3, 7)$
D $(4, 5)$