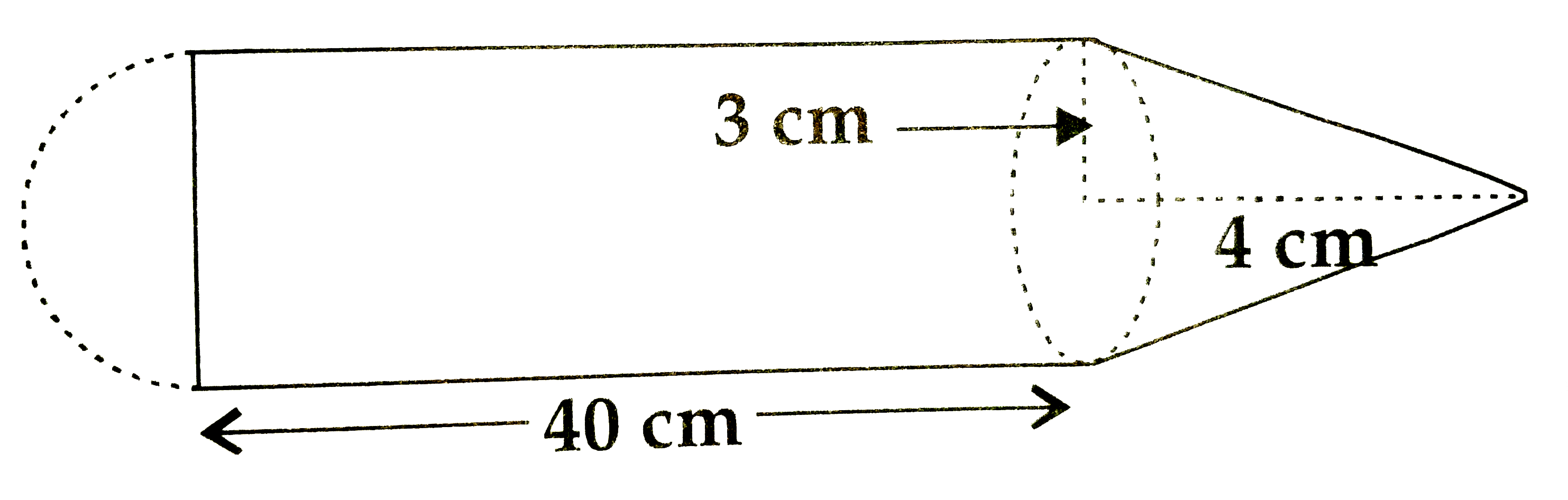In the figure, a toy made from a hemisphere, a cylinder and cone is shown. Find the total area of the toy.
The correct Answer is:Total area of the toy is 273πcm2.
Step by step video & image solution for In the figure, a toy made from a hemisphere, a cylinder and cone is shown. Find the total area of the toy. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A toy is in the form of a cone surmounted by a hemisphere whose radius is 3.5cm . If the total height of the toy is 15.5cm then find its total surface area and the Volume
A214.5cm2and240cm3B240cm2and214.5cm3C214.5cm2and243.83cm3D243.83cm2and214.5cm3A toy is in the form of a cone mounted on a hemisphere of radius 7 cm. The total height of the toy is 14.5 cm. Find the volume of the toy. (Take π= 22/7)
A539/6 cm3B3311/3 cm3C847/6 cm3D200 cm3
A toy is in the form of a cone mounted on a hemisphere of same radius 7 cm. If the total height of the toy is 31cm, find the total surface area.
View SolutionThe figure shows a toy Its lower part is a hemisphere and the upper part is a cone. Find the volume and the surface area of the toy from the measures shown in the figure. (π=3.14)

View SolutionA toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. The total height of the toy is 15.5 cm find the total surface area and volume of the toy.
View SolutionA solid cylinder of diamter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right circular cone mounted on a hemisphere. Find the radius of the hemisphere and the total height of the toy, if the height conical part is thrice its radius.
View SolutionThe given figure shows a toy. Its lower part is a hemisphere and the upper part is a cone. Find the volume and the surface area of the toy from the measures shown in the figure.

View SolutionA toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21cm and its volume is 2/3 of the volume of the hemisphere, calculate the height of the cone and the surface area of the toy. (Useπ=227).
View Solution