Explain with a diagram : Kepler's three laws. Hence show that gravitational force, F∝1r2 (in the usual notation).
Kepler's first law :
The orbit of a planet is an ellipse with the Sun at one of the foci.
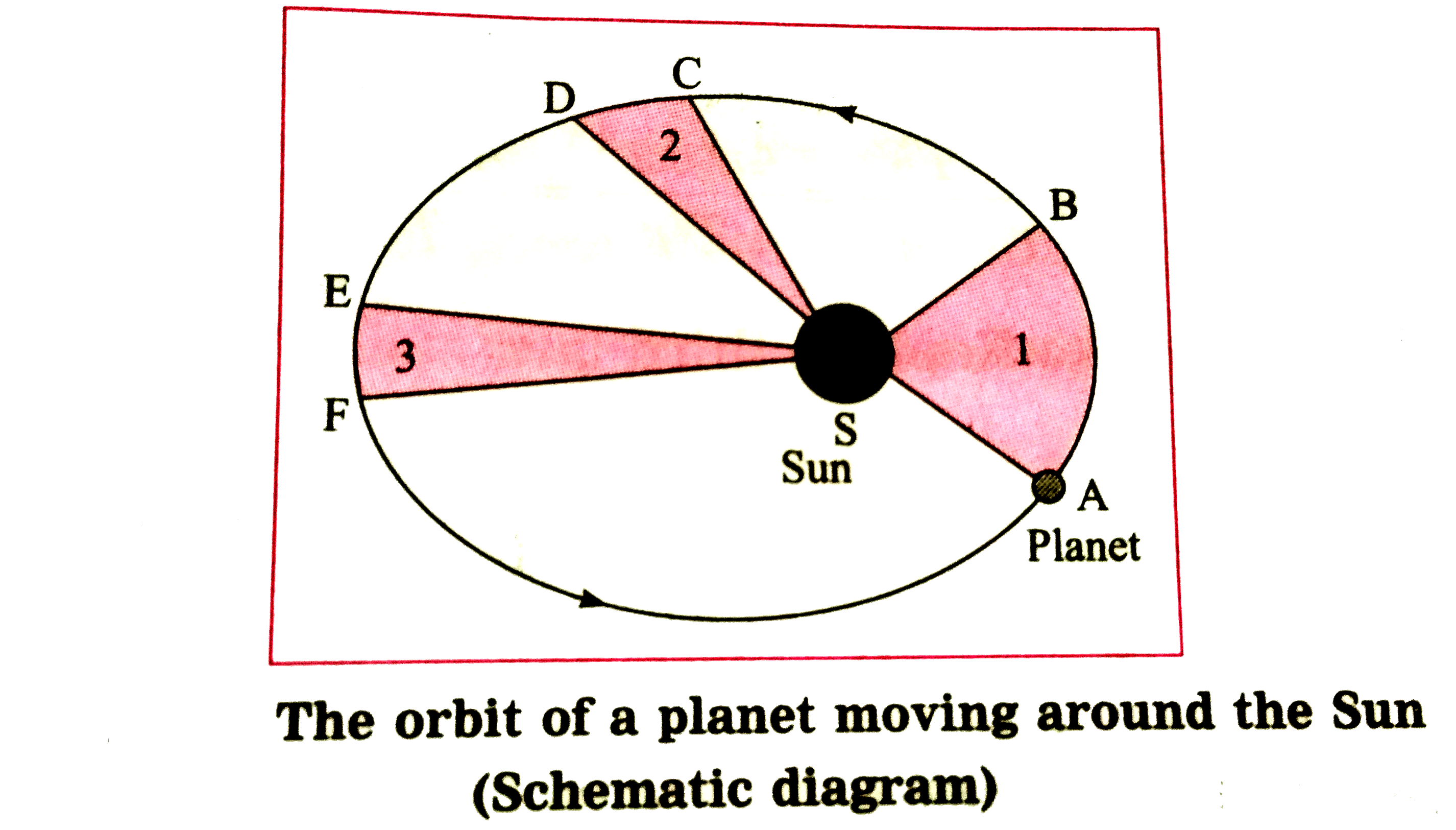
Figure 1.5 shows the elliptical orbit of a planet revolving around the Sun (S).
Kepler's second law :
The line joining the planet and the Sun sweeps equal areas in equal intervals of time.
A→B,C→DandE→F are the displacements of the planet in equal intrvals of time.
The straight lines AS, CS and ES sweep equal areas in equal areas in equal intervals of time.
Area ASB = area CDS = area ESF.
Kepler's third law :
The square of hte period of revolution of a planet around the Sun is directly proportional to the cube of the mean distance of the planet from the Sun.
Thun, if r is the average distance of the planet from the Sun and T is its period of revoltuion, then,
T2∝r3, i.e., T2r3=constant = K
For simplicity we shell assume the orbit to be a circle. In Fig. 1.6, S denotes the position to the Sun, P denotes the position the position of a planet at a given instant and r denotes the radius of the orbit (≡ the distance of the planet from the Sun). Here the speed of the planet is uniform. It is

v=circumference of the circleperiod of revoltuion of the planet
=2πrT.
If m is the mass of the planet, the centripetal force exerted on the planet by the Sun (≡ gravitational force), F=mv2r
∴F=m(2πr/T)2r=4π2mr3T2r=4π2mrT2
According to Kepler's third law,
T2=Kr3
∴F=4π2mrKr3=4π2mK(1r2)
Thus, F∝1r2 as 4π2mK is constant in a particular case.
Topper's Solved these Questions
- GRAVITATION BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GRAVITATION EXERCISE - Give scientific reasons :
3 Videos
- GRAVITATION BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GRAVITATION EXERCISE - Distinguish between :
2 Videos
- GRAVITATION BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GRAVITATION EXERCISE - QUESTIONS & ANSWERS
45 Videos
- GIVE SCIENTIFIC REASONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - GIVE SCIENTIFIC REASONS EXERCISE - CHAPTER 10 : DISASTER MANAGEMENT
2 Videos
- HEATBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - HEATEXERCISE - NUMERICAL PROBLEMS FOR PRACTICE
12 Videos
Similar Questions
Knowledge Check
According to kepler's third law, with usual notation:
AT2/R2=constantBR2/T3CT2/R3=constantDall the three aboveKepler's third law states that square of period revolution (T) of a planet around the sun is proportional to third power of average distance i between sun and planet i.e. T2=Kr3
here K is constant
if the mass of sun and planet are M and m respectively then as per Newton's law of gravitational the force of alteaction between them is F=GMmr2, here G is gravitational constant. The relation between G and K is described asAGK=4π2BGMK=4π2CK=GDK=1GKepler's third law states that square of period revolution (T) of a planet around the sun is proportional to third power of average distance i between sun and planet i.e. T2=Kr3
here K is constant
if the mass of sun and planet are M and m respectively then as per Newton's law of gravitational the force of alteaction between them is F=GMmr2, here G is gravitational constant. The relation between G and K is described asAGMK=4π2BK=GCK=1GDGK=4π2
State the Kepler's law which is represented by the relation r3∝T2
View SolutionKepler's third law states that square of period revolution (T) of a planet around the sun is proportional to third power of average distance i between sun and planet i.e. T2=Kr3
here K is constant
if the mass of sun and planet are M and m respectively then as per Newton's law of gravitational the force of alteaction between them is F=GMmr2, here G is gravitational constant. The relation between G and K is described as
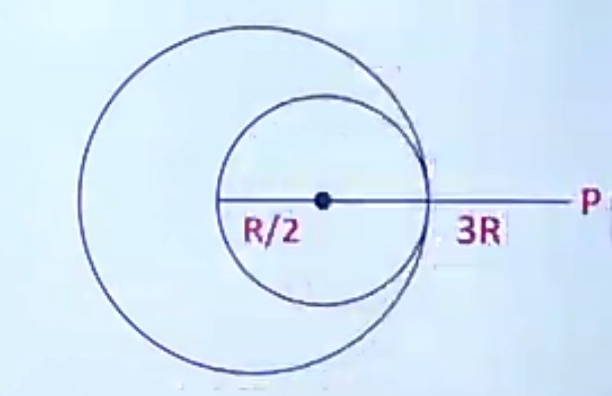
View SolutionA solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at a distance 3R from the center of the sphere. The 1 sphere with the cavity now applies a gravitational force F2, on the same particle. Then ratio F1F2 is
View SolutionWith usual notation in ΔABC,rr1r2r3 is equal to
View SolutionIn an equilateral triangle with usual notations the value of 27r2Rr1r2r3is equal to
View Solution
